시간복잡도

Vorhandenheit ·2021년 12월 10일

알고리즘과 자료구조

목록 보기

7/16

시간 복잡도

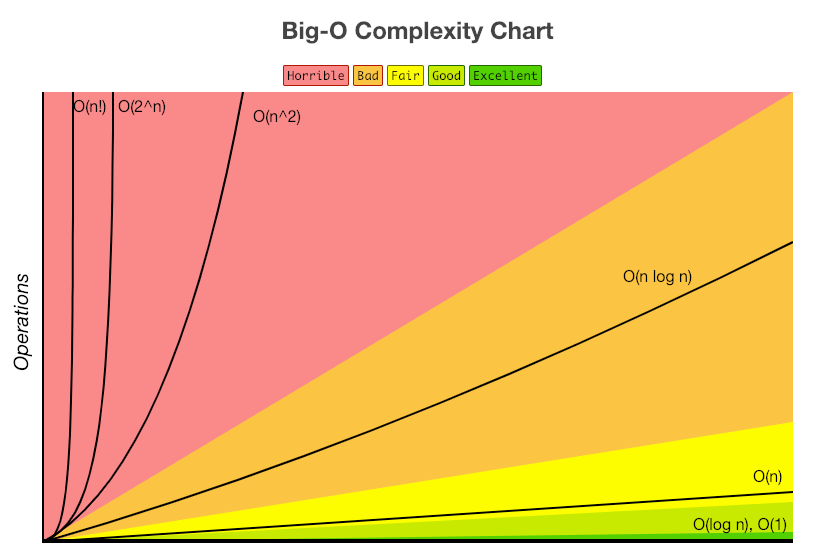
입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가

빅-오 표기법을 사용해 시간복잡도를 나타냄

시간 복잡도: 알고리즘의 수행시간을 평가
공간 복잡도: 알고리즘 수행에 필요한 메모리 양을 평가

Big-O 표기법

입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가?

최상의 경우 : 오메가 표기법 (Big-Ω Notation)
평균의 경우 : 세타 표기법 (Big-θ Notation)
최악의 경우 : 빅오 표기법 (Big-O Notation)

시간 복잡도 표기

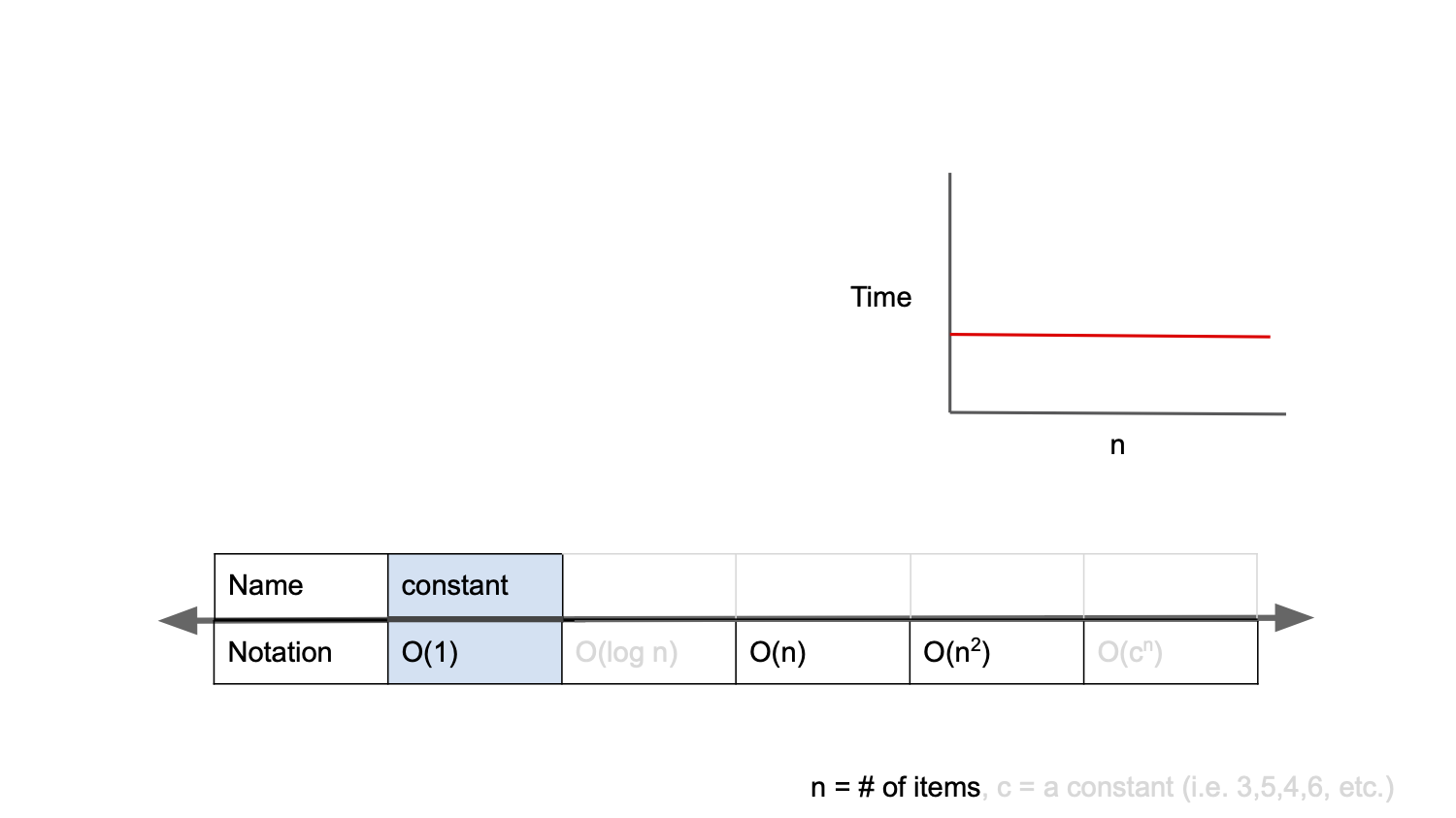
1. O(1) 상수 시간

const example = [1,2,3,4,5];
function findO1(example) {
  console.log(example[0]); // O(1)
  console.log(example[1]); // O(1)
}
findO1(example);

입력값의 크기가 아무리 커져도 즉시 출력 가능

2. 0(n) 상수 시간

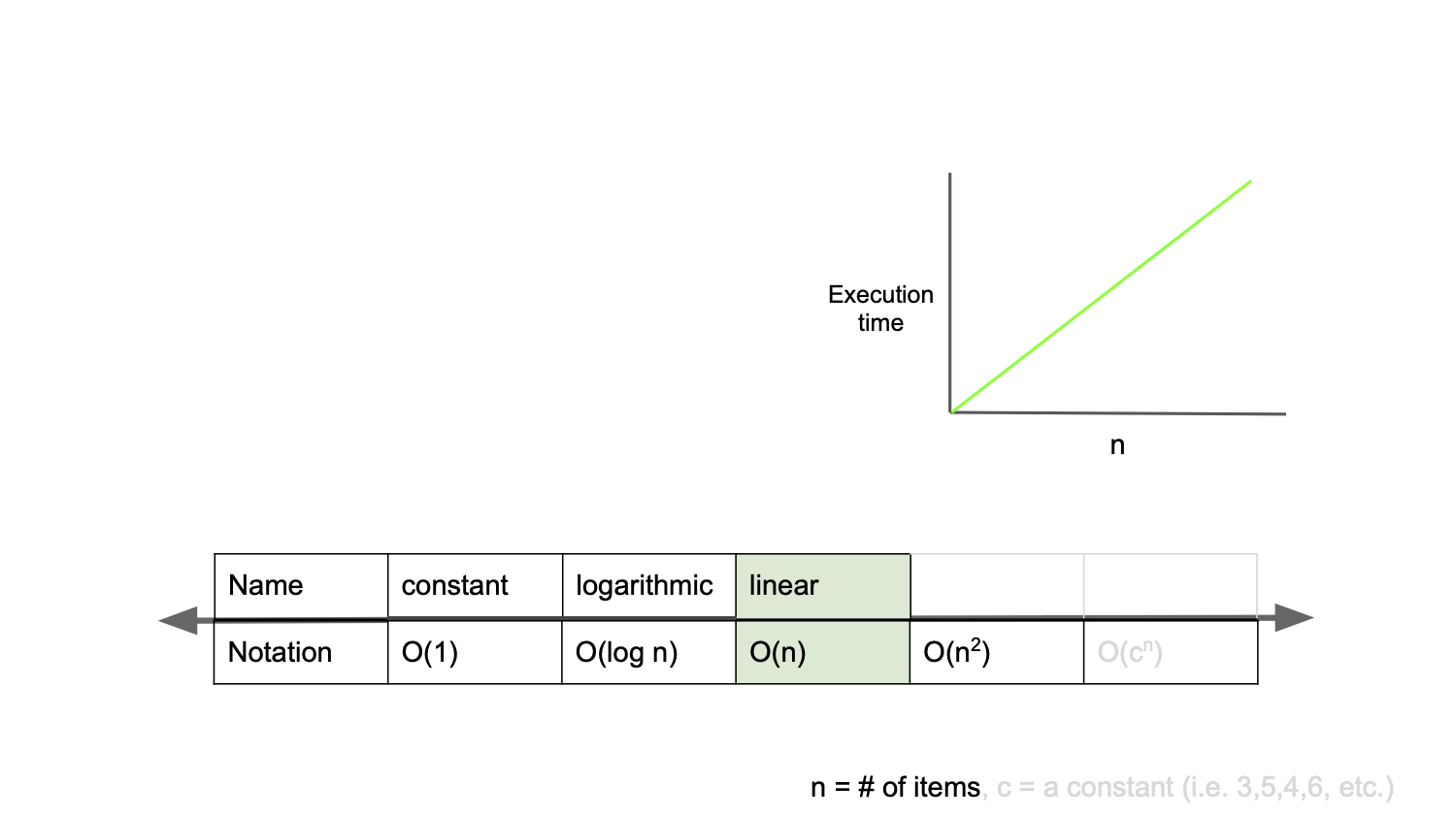
linear complexity라고 부르며, 입력값이 증가함에 따라 시간 또한 같은 비율로 증가하는 것을 의미

function O_n_algorithm(n) {
	for (let i = 0; i < n; i++) {
	// do something for 1 second
	}
}

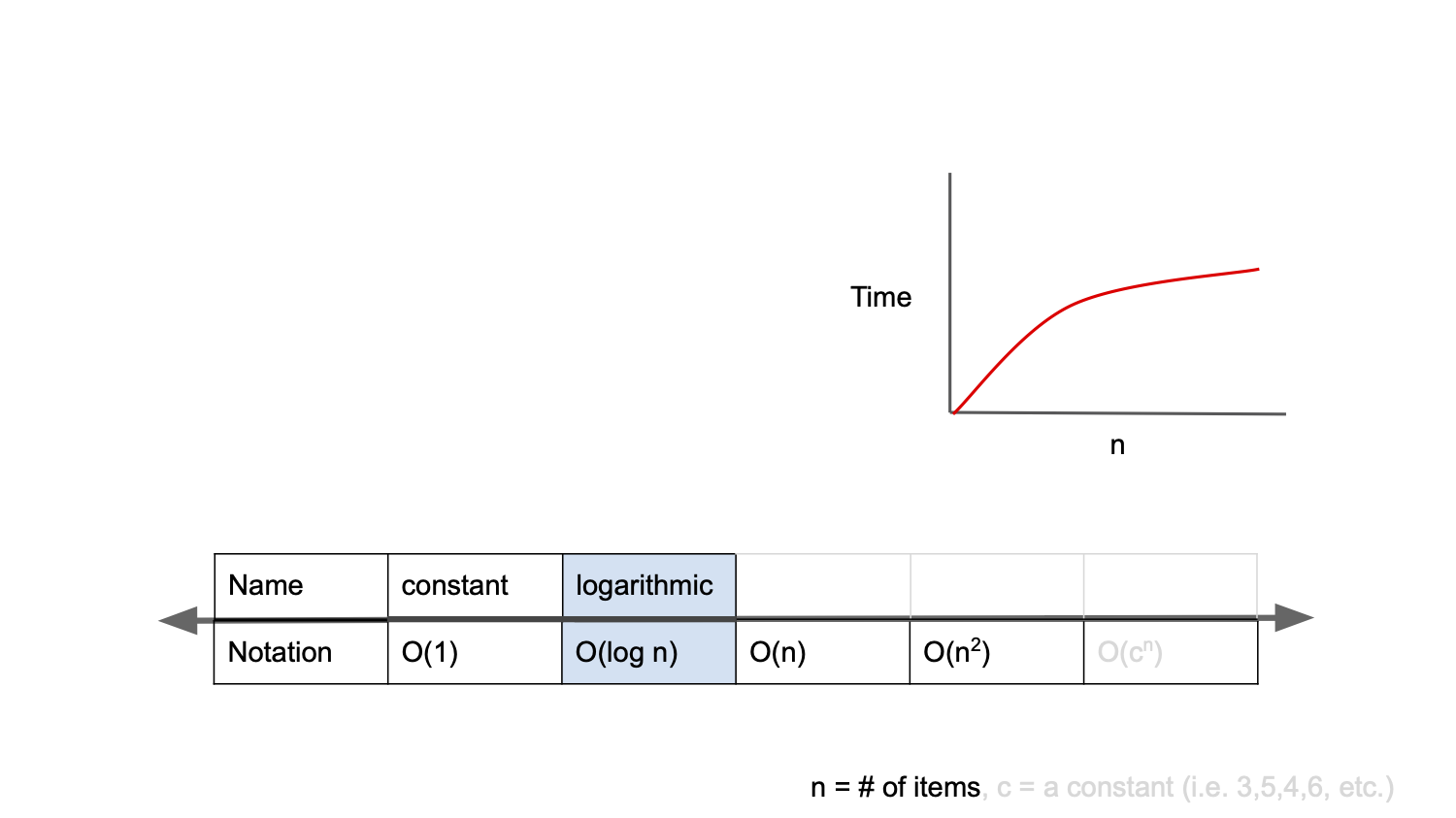
3. O(log n) 상수 시간

let arr = []; function log(k, s, e){
  for(let i = s; i <= e; i++) {
    arr.push(i); let m = (s+e)/2;
    if(arr[m] === k){
      console.log(m)
    }
    else if(arr[m]> k) {
      return log(k, s, m-1);
    } 
    else{
      return log(k, m+1,e)
    }
  }
}

logarithmic complexity 라고 부르며, O(1) 다음으로 빠른 시간복잡도를 가집니다. 대표적 알고리즘은 이진 검색입니다.

4. O(n2) 상수 시간

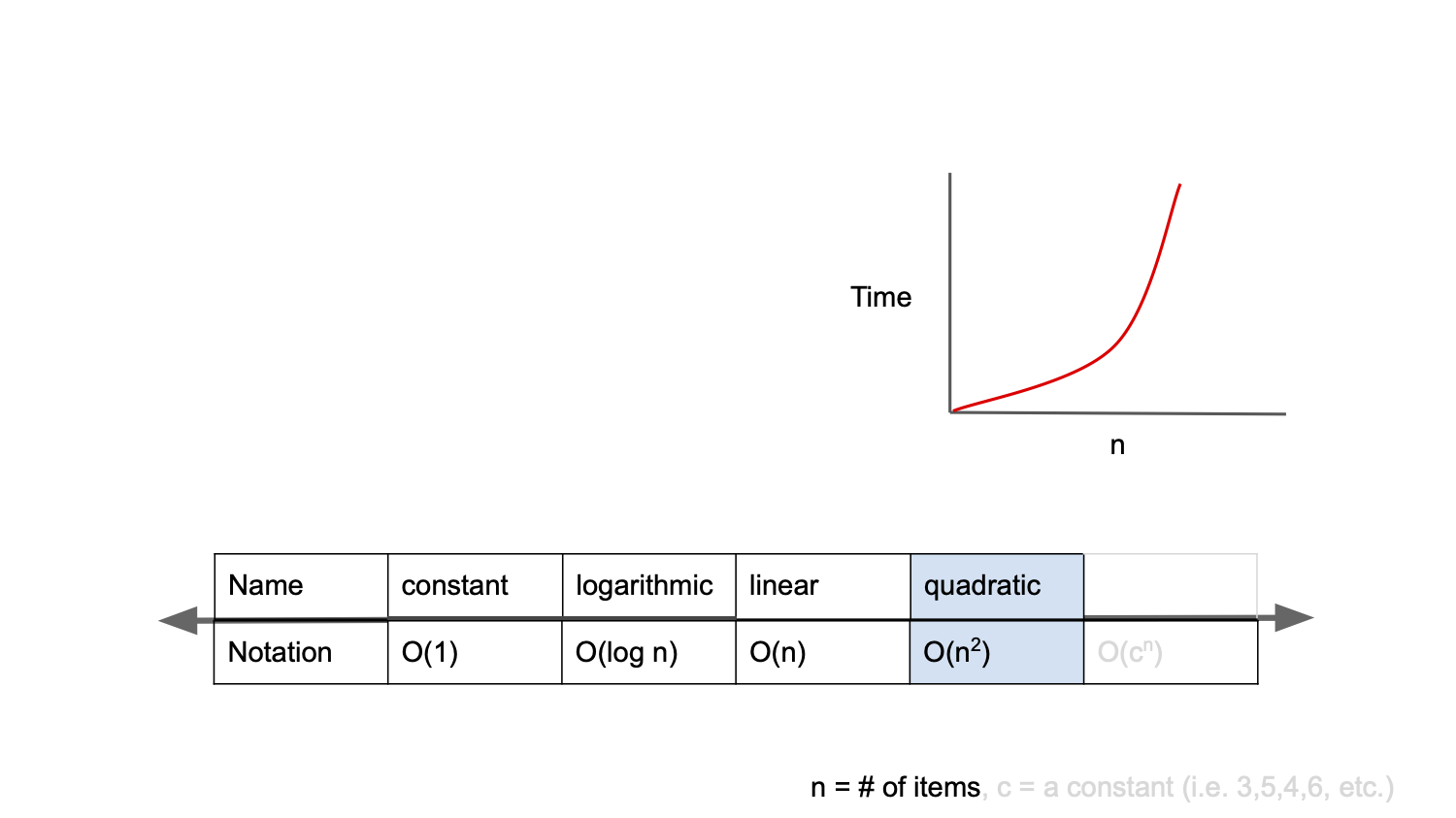
quandratic complexity라고 부르며, 입력 값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 것을 의미( 이중 반복문)

function O_quadratic_algorithm(n) {
	for (let i = 0; i < n; i++) {
		for (let j = 0; j < n; j++) {
		// do something for 1 second
		}
	}
}

5. O(2n) 상수 시간

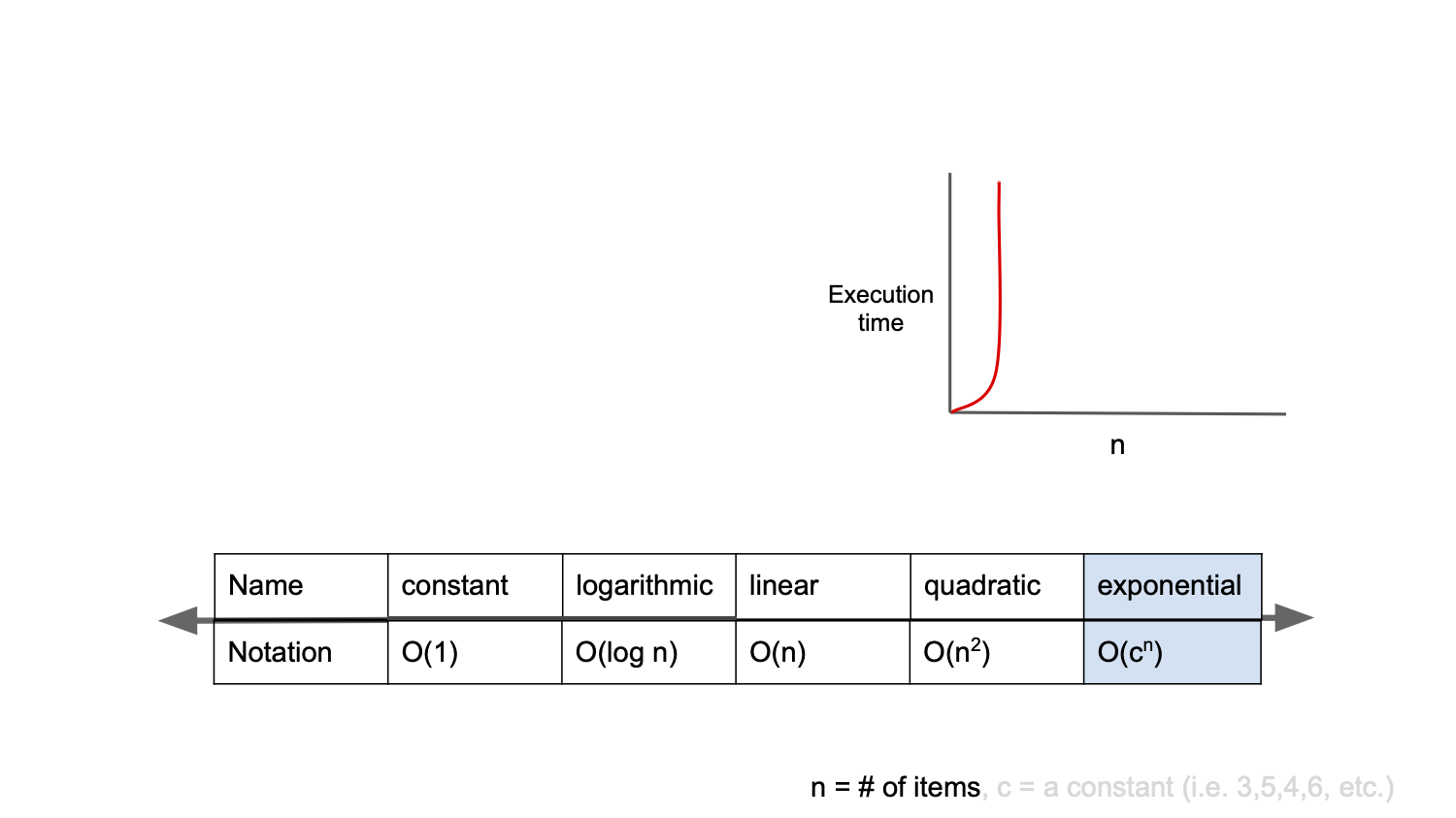
exponential complexity 라고 부르며, 가장 느린 시간 복잡도입니다. 대표적 알고리즘은 재귀로 구현한 피보나치수열입니다.

function fibonacci(n) {
	if (n <= 1) {
		return 1;
	}
	return fibonacci(n - 1) + fibonacci(n - 2);
}

Big-O 계산 규칙

1. Worst Case

Big-O를 계산할 때는 항상 최악의 상황을 고려해야 합니다.

const nemo = ['nemo'];
const everyone = ['dory', 'bruce', 'marlin', 'nemo', 'gill', 'bloat', 'nigel', 'squirt', 'darla', 'hank'];
const large = new Array(10000).fill('nemo');

findNemo = (array => {
  for (let i = 0; i < array.length; i++) {
    if (array[i] === 'nemo') {
      console.log("Found NEMO");
    }
  }
});

findNemo(everyone);

4번째 위치에서 답을 찾을 수 있지만, 마지막에 위치했을 경우 시간복잡도는 O(n) 이된다. 시간복잡도는 항상 최악의 경우를 고려해야만한다

2. Remove Constants

Big-O를 계산할 때는 상수를 제거하라는 의미

function printFirstItemThenFirstHalfThenSayHi100Times(items) {
  console.log(items[0]); // O(1)
  
  var middleIndex = Math.floor(items.length / 2);
  var index = 0;
  
  while (index < middleIndex) { // O(n/2)
    console.log(items[index]);
    index++;
  }
  
  for (var i = 0; i < 100; i++) { // O(100)
    console.log('hi');
  }
}

시간복잡도는 O(1 + n/2 + 100)이지만 최악의 상황을 고려하면 상수를 제거하고 시간복잡도는 O(n)이 된다.

3. Different Terms for Inputs

function compressBoxesTwice(boxes, boxes2) {
  boxes.forEach(function(boxes) { // O(a)
    console.log(boxes);
  });
  boxes2.forEach(function(boxes2) { // O(b)
    console.log(boxes);
  });
}

매개변수가 다를 경우에는 계산을 따로 해줘야 하기 때문에 시간복잡도는 O(a+b)이다.

4. Drop Non Dominants

function printAllNumbersThenAllPairsSums(numbers) {
  console.log('these are the numbers');
  numbers.forEach(function(number) { // O(n)
    console.log(number);
  });
  
  console.log('and these are their sums');
  numbers.forEach(function(firstNumber) { 
    numbers.forEach(function(secondNumber) {
      console.log(firstNumber + secondNumber); // O(n^2)
    });
  });
}
printAllNumbersThenAllPairsSums([1,2,3,4,5]);