GCM & LCM

최대 공약수 (Greatest Common Division)

• 두 수 A와 B 공통된 약수 중에서 가장 큰 정수

let getGCD = (num1, num2) => {
	let gcd = 1;
  
  for (let i = 2; i <= Math.min(num1, num2); i++) {
  if (num % i === 0 && num2 & i === 0) { // 나누어지는게 겹친다면
  	gcd = i;
  		}
    }
  return gcd
}

유클리드 호제법

유클리드 호제법의 기본 원리는 num1를 num2로 나눈 나머지를 r이라고 했을 때, GCD(num1, num2) = GCD(num2, r)과 같다는 것이다

let getGCD = (num1, num2) => (num2 > 0 ? getGCD(num2, num1 % num2) : null)

let getGCD2 = (num1, num2) => {
	while (num2 > 0) {
    	let r = num1 % num2;
      	num1 = num2
      	num2 = r
    }
  return null
}

최소 공배수 (Least Common Multiple)

• 두 수, 공통인 배수 중 가장 작은 수

let getLCM = (num1, num2) => {
	let lcm = 1;
  
  while (true) {
  	if ((lcm % num1 === 0) && (lcm % num2 === 0)) {
    	break;
    }
    lcm++
  }
  return lcm
}

유클리드

let lcm = a * b/ gcd(a,b)

let getLcm2 = (num1, num2) => {
	let rest
    while (num2 !== 0) {
    	rest = num1 % num2
      num1 = num2
      num2 = rest
    }
  return num1
}

멱집합

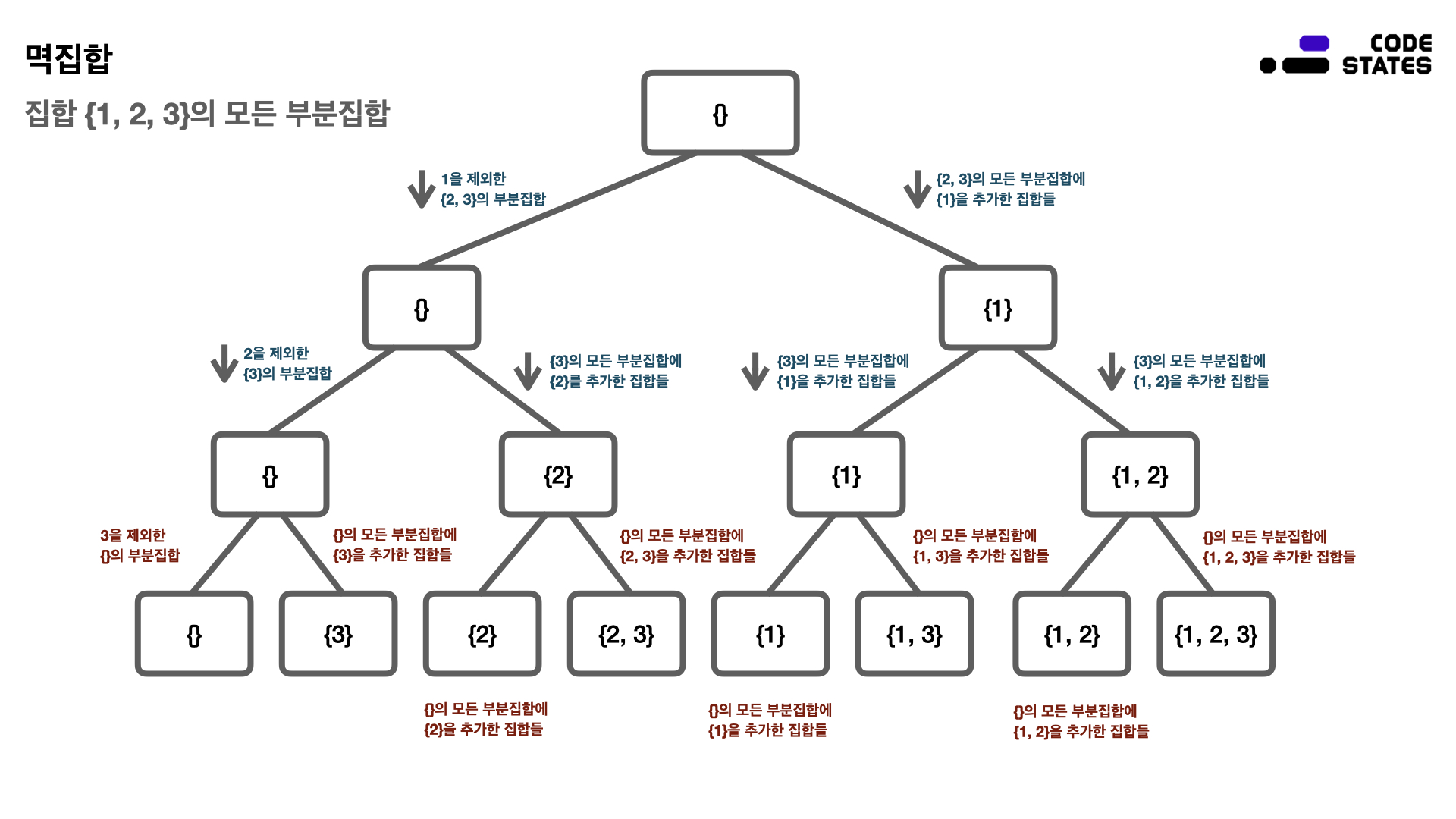
• 주어진 집합의 모든 부분집합
  dfs 응용한다

function powerSet(arr) {
	let check = new Array(arr.length).fill(false);
  	let powerSetArr = [];
  
  const dfs = (depth) => {
  	if (depth === check.length) {
    	powerSetArr.push(arr.filter((v, idx) => check[idx]))
    }
    else {
    	check[depth] = true;
      dfs(depth +1)
      check[depth] = false;
      dfs(depth+1);
    }
  }
  dfs(0)
  return powerSetArr
}