다익스트라 알고리즘(Dijkstra Algorithm)

Vorhandenheit ·2022년 3월 9일

알고리즘과 자료구조

목록 보기

11/16

다익스크라 알고리즘

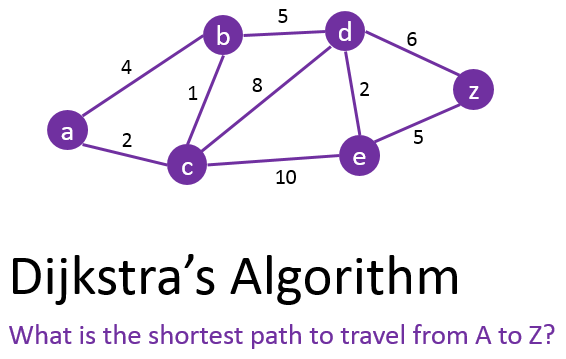
다익스트라 알고리즘은 대표적인 최단 경로 탐색 알고리즘입니다. 하나의 시작 정점에서 다른 모든 정점까지 최단 경로를 구합니다. 이때 음의 가중치를 갖는 간선은 허용하지않습니다.

다익스트라 알고리즘은 동적 프로그래밍(DP)를 활용한 최단 경로 탐색 알고리즘입니다. DP인 이유는 '최단 거리는 여러 개의 최단 거리로 이루어져있기 때문입니다.'

1. 성능

총 O(V)번에 걸쳐서 최단 거리가 가장 짧은 노드를 매번 선형 탐색해야합니다.
=> 따라서 전체 시간 복잡도는 O(V^2)입니다.
=> 힙 자료구조를 이용하는 다익스트라 알고리즘 시간 복잡도는 O(Elog V)입니다.

알고리즘 원리

출발 노드를 선정

최단 거리 테이블 초기화

방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택

해당 노드를 거쳐 다른 노드로 가는 비용을 계산해 최단 거리 테이블을 갱신

3, 4번 과정을 반복합니다.

2. 동작과정

(1) 그래프를 준비하고 출발 노드를 선정

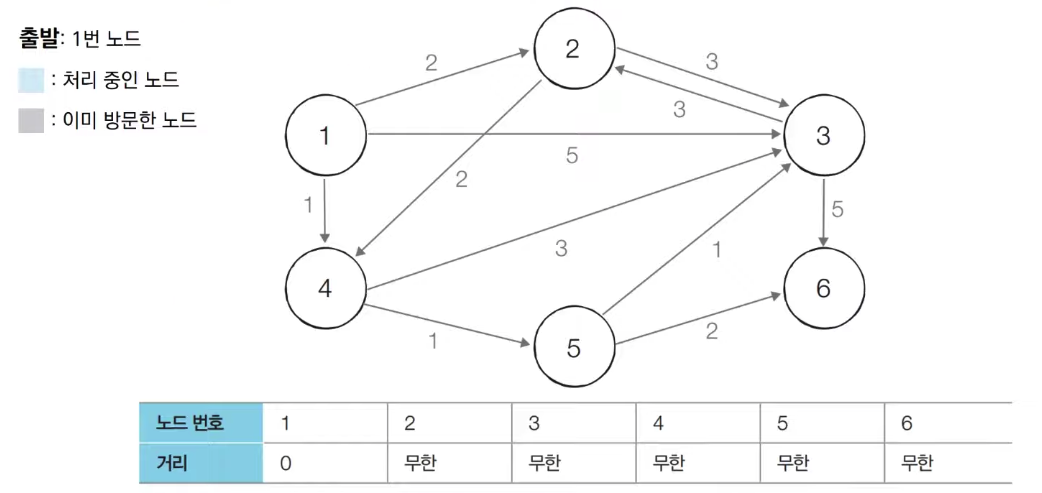
(2) 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드인 1번노드를 처리합니다.

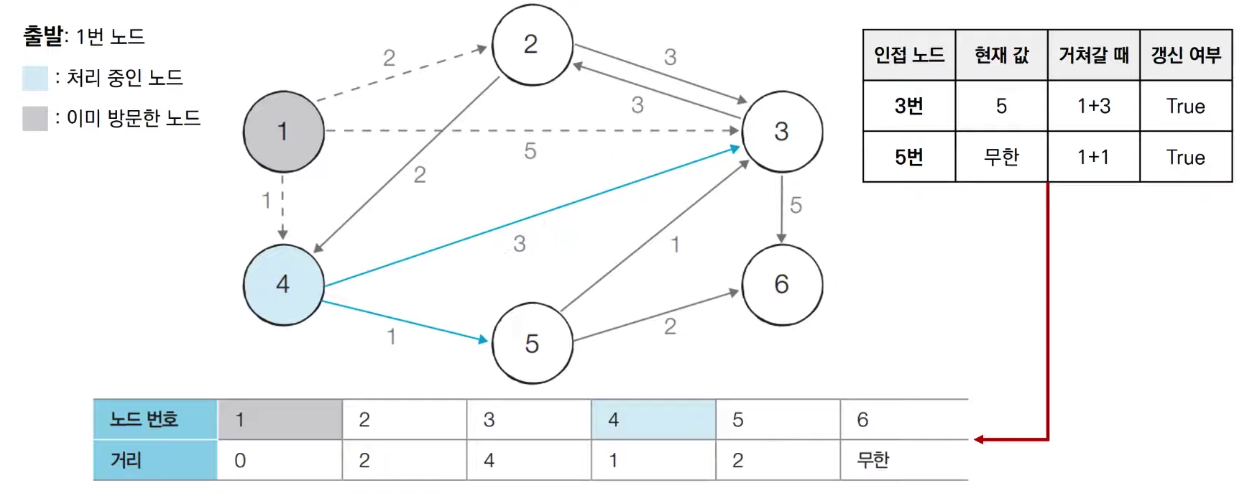
(3) 방문하지않는 노드 중에서 최단 거리가 가장 짧은 노드인 2번을 처리합니다.

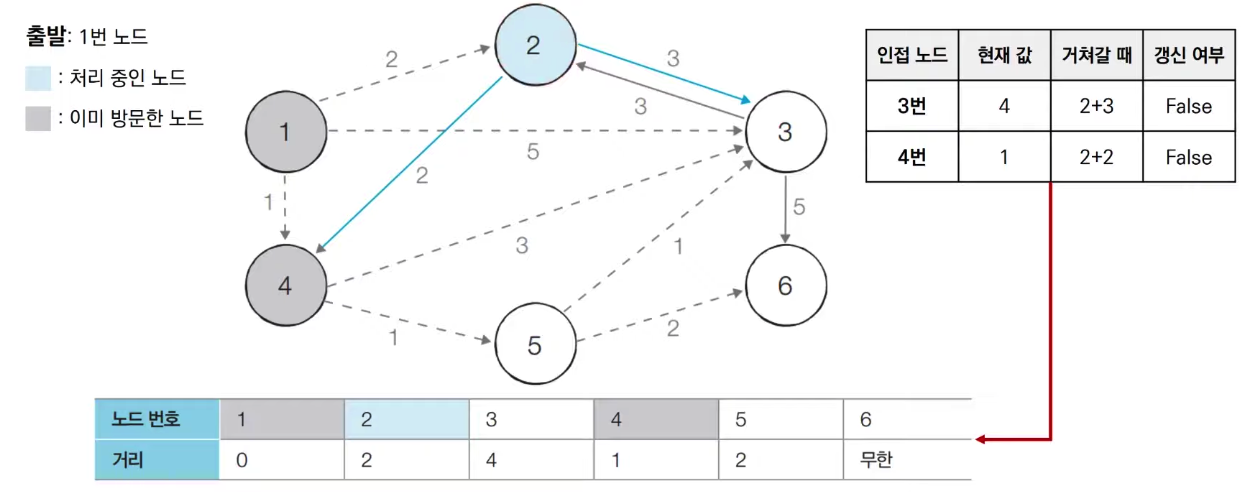
(4) 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드인 5번 노드를 처리합니다.

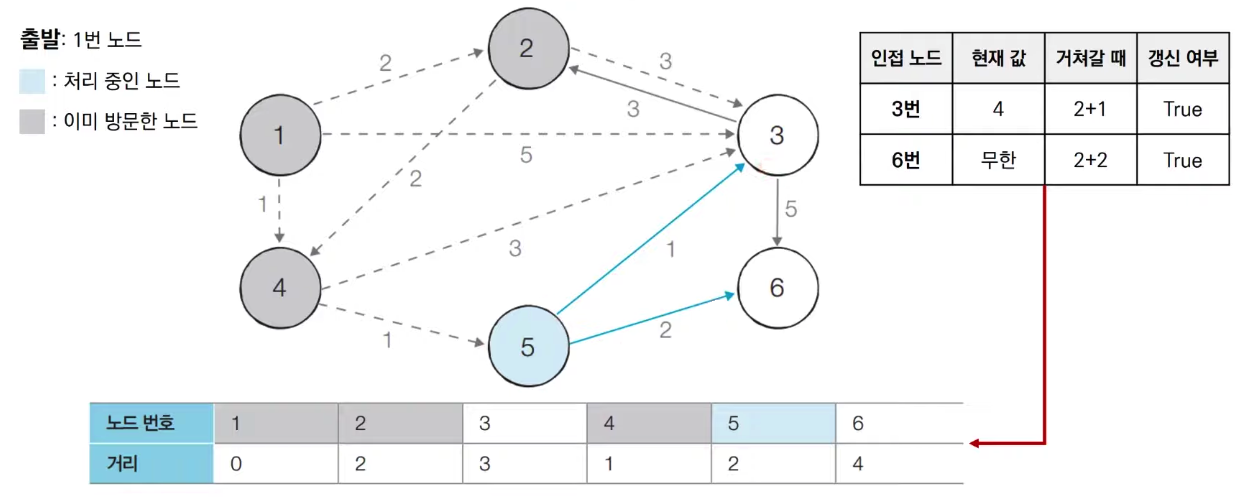
(5) 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드인 3번 노드를 처리합니다.

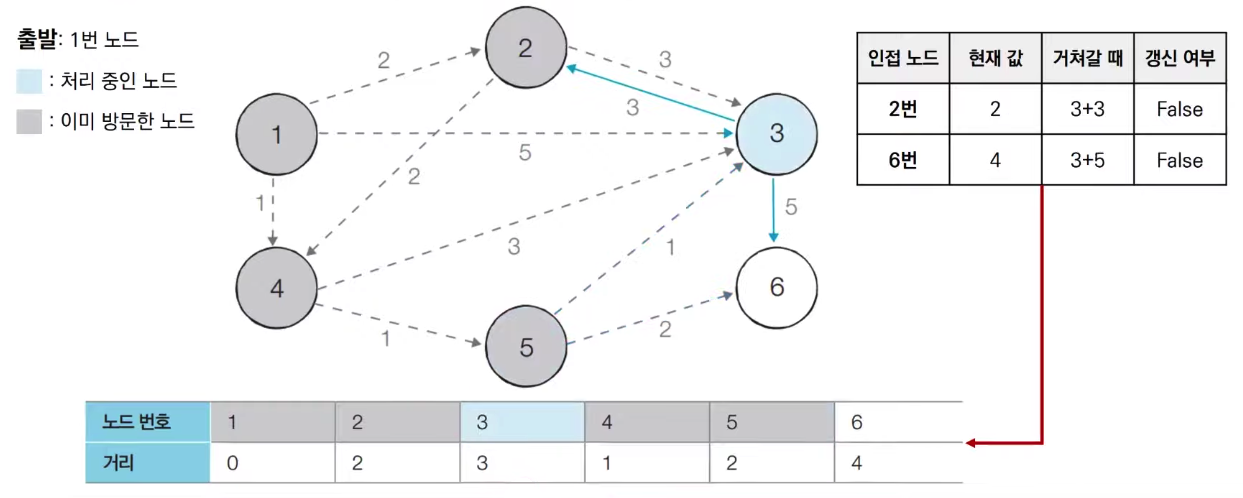
(6) 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드인 6번 노드를 처리합니다.

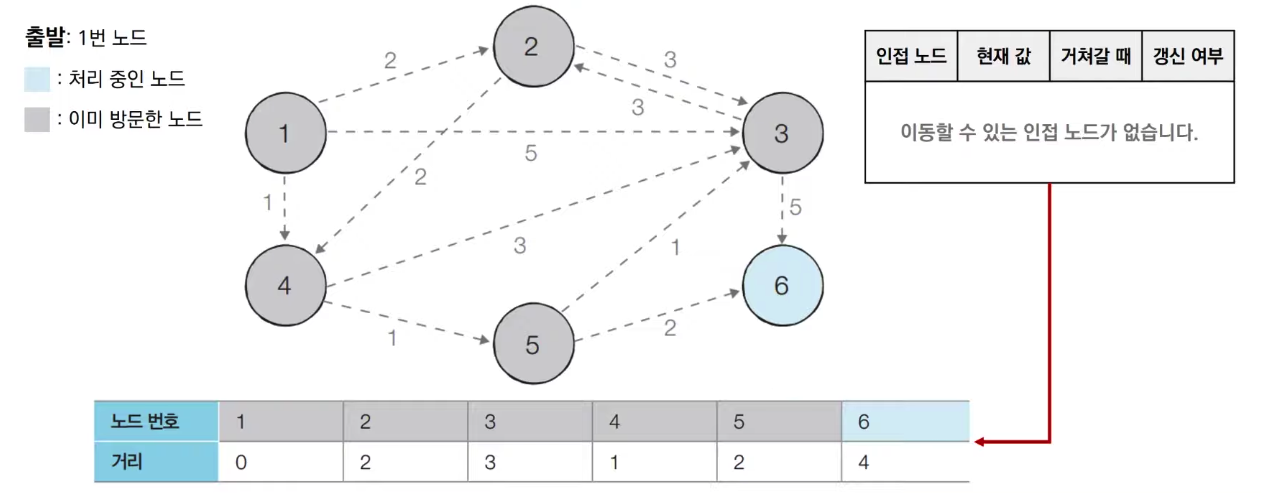
3. 예시

function createGraphByList(num , edges) { // 연결 리스트로 그래프 구현
	const edgesList = {};
  	for (let i = 1; i <= num; i++) { //num 은 정점의 수
    	edgesList[i] = [];
    }
  	edges.forEach(([src, dst, weight]) => {
      //무방향 그래프이므로 양쪽 모두에 간선을 추가합니다.
    	edgesList[src].push({ node: dst, weight: weight });
      	edgesList[dst].push({ node: src, weight: weight })
    }) //weight 거리, 가중치를 뜻합니다
  return edgesList
}

function createGraphByMatrix(num, edges) {
	const matrix = [];
  	const INF = 101;
  for (let row = 0; row <= num; row++) {
    matrix.push(Array(num+1).fill(INF));
  }
  // 최단 거리를 구해야하기 떄문에 간선이 없는 구간의 거리는 무한대로 간주합니다.
  // 자기 자신과의 거리는 0입니다.
  edges.forEach(([src, dst, weight]) => {
  	//무방향 그래프이므로 양쪽 방향 모두에 간선을 추가합니다.
    matrix[src][dst] = matrix[dst][src] = weight;
  })
  return matrix;
}

function Dijkstra(num, edges, start, end) {
	const matrix = createGraphByMatrix(num, edges) // 그래프 생성
  	const dist = matrix[start].slice(); // 최단 거리를 저장하는 배열
  	const visited = Array(num+1).fill(false) //방문 표시
    visited[start] = true;
  
  const before = Array(num + 1).fill(-1);
  edges.forEach(([src, dst]) => {
  	if (src === start) before[dst] = src;
    if (dst === start) before[src] = dst;
  })
  const getNext = (dist) => {
  	let min = Number.MAX_SAFE_INTEGER
    for (let i = 1; i <= num; i++) {
    	if (dist[i] < min && visited[i] === false) {
        	min = dist[i];
          	target = i;
        }
    }
    return target;
  }
  for (let round = 0; round < num -2; round++) {
  	const nearest = getNext(dist);
    visited[nearest] = true;
    visited.forEach((calculated, v) => {
    	if (calculated === false) {
        	if (dist[nearest] + matrix[nearest][v] < dist[v]) {
            	dist[v] = dist[neareset] + matrix[nearest][v];
              before[v] = nearest;
            }
        }
    })
  }
  function getPath(before, start, end) {
  	let vertex = before[end];
    const path = [end, vertex];
    while (vertex !== start) {
    	vertex = before[vertex];
      	path.push(vertex);
    }
    return path.reverse()
  }
  const path = getPath(before, start, end);
  return dist[end]
}