벨만-포드 알고리즘

Vorhandenheit ·2022년 3월 10일

알고리즘과 자료구조

목록 보기

13/16

벨만-포드 알고리즘(Bellman-Ford Algorithm)

벨만 보드 알고리즘은 다익스트라 알고리즘과 같이 한 정점으로부터 다른 모든 정점으로 최단경로를 찾는 알고리즘입니다. 차이점은 음수 간선이 포함된 상황에서 최단 거리를 계산할 때 사용합니다.

다익스트라 알고리즘 한계

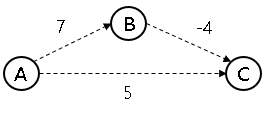
A => C로 갈때 두 가지 경로가 존재합니다.

A => B => C : 3
A => C : 5
1번이 더 짧지만, 다익스트라 알고리즘에서는 1번의 최단거리를 5로 확정합니다. 다익스트라 구현 조건 자체가 가중치는 양의 정수이기 떄문입니다.

1. 동작 과정

(1) 출발 노드를 선정합니다.
(2) 최단 거리 테이블을 초기화합니다.
(3) 다음의 과정을 N-1번 반복합니다.
- 1. 전체 간선 E개를 하나씩 확인합니다.
- 2. 각 간선을 거쳐서 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신합니다.

(4) N번째 조회: 만약 음수 간선 순환이 발생하는지 체크하고 싶다면 3번의 과정을 한번 더 수행합니다.

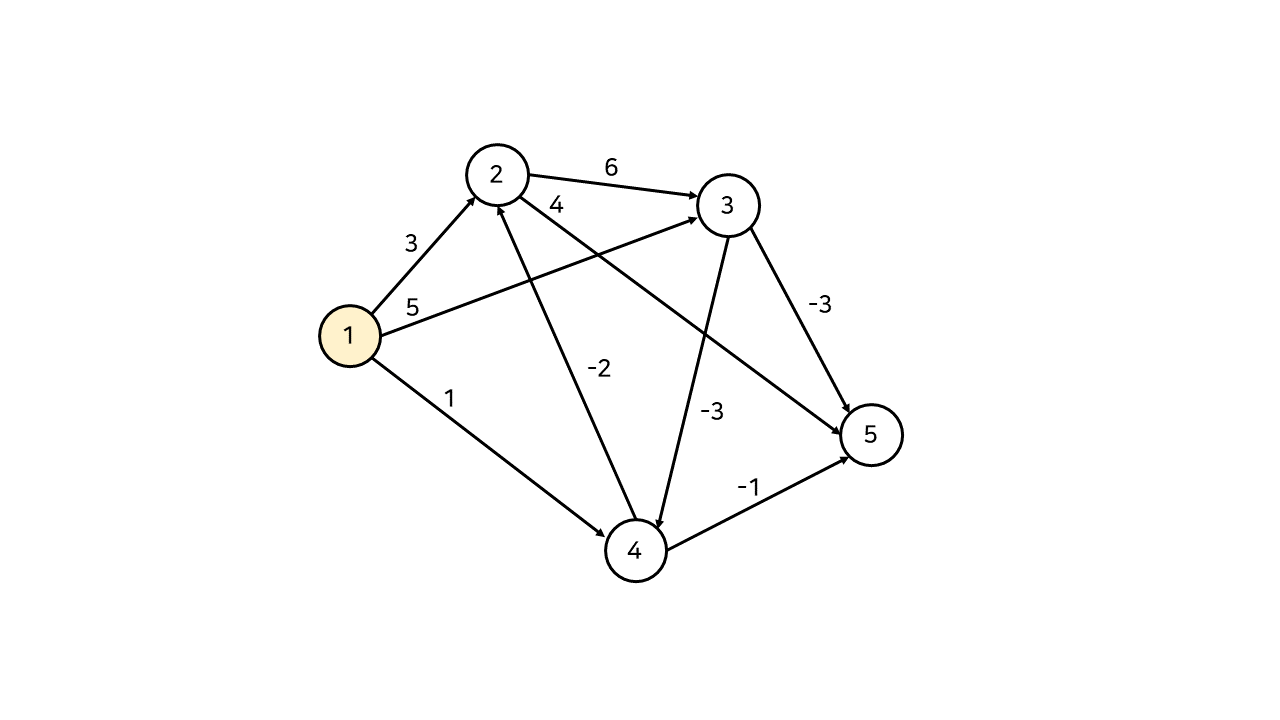
2. 동작 설명

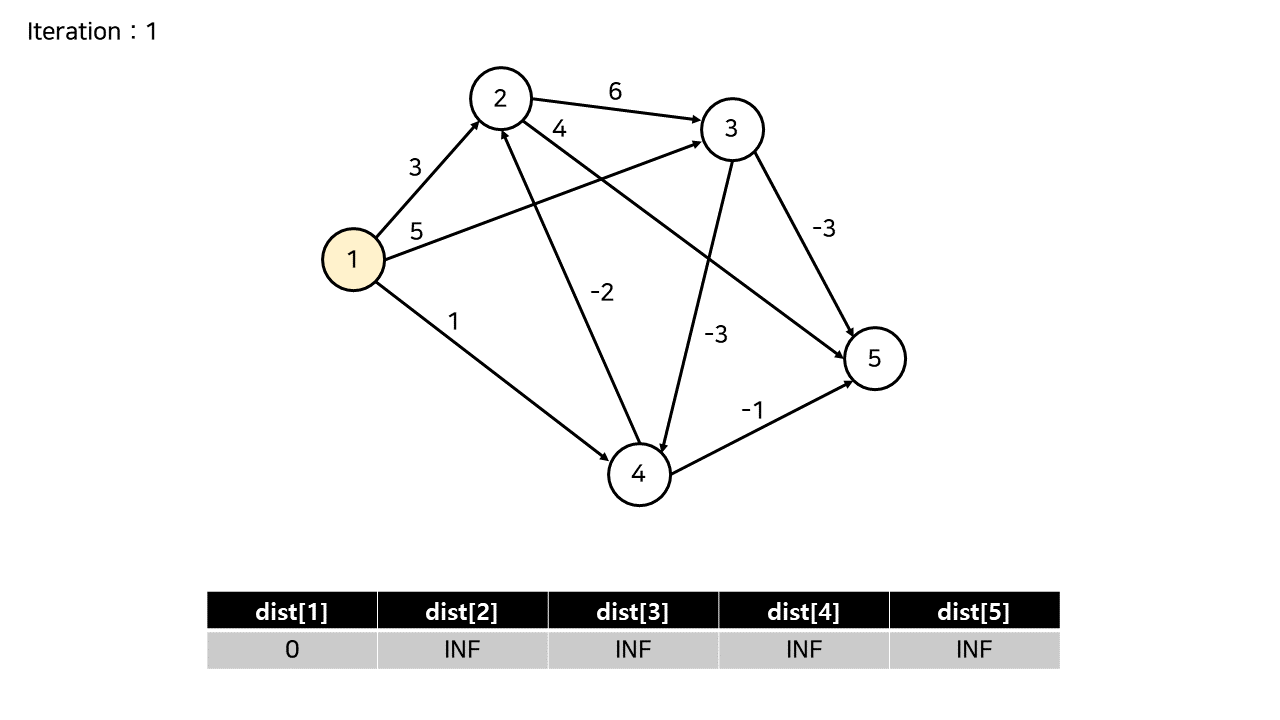
(1) 초기화

(2) 정점 1

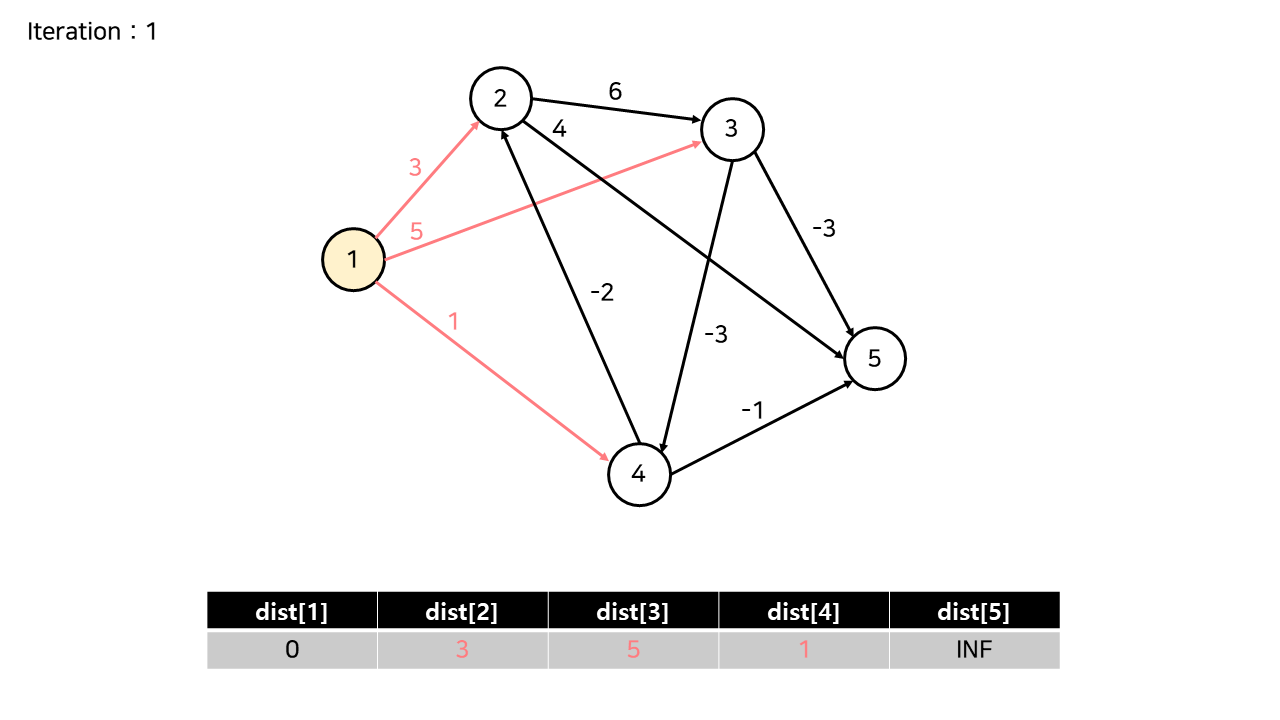
2,3,4 번 노드가 연결되어있어 갱신되었습니다.

(3) 정점 2

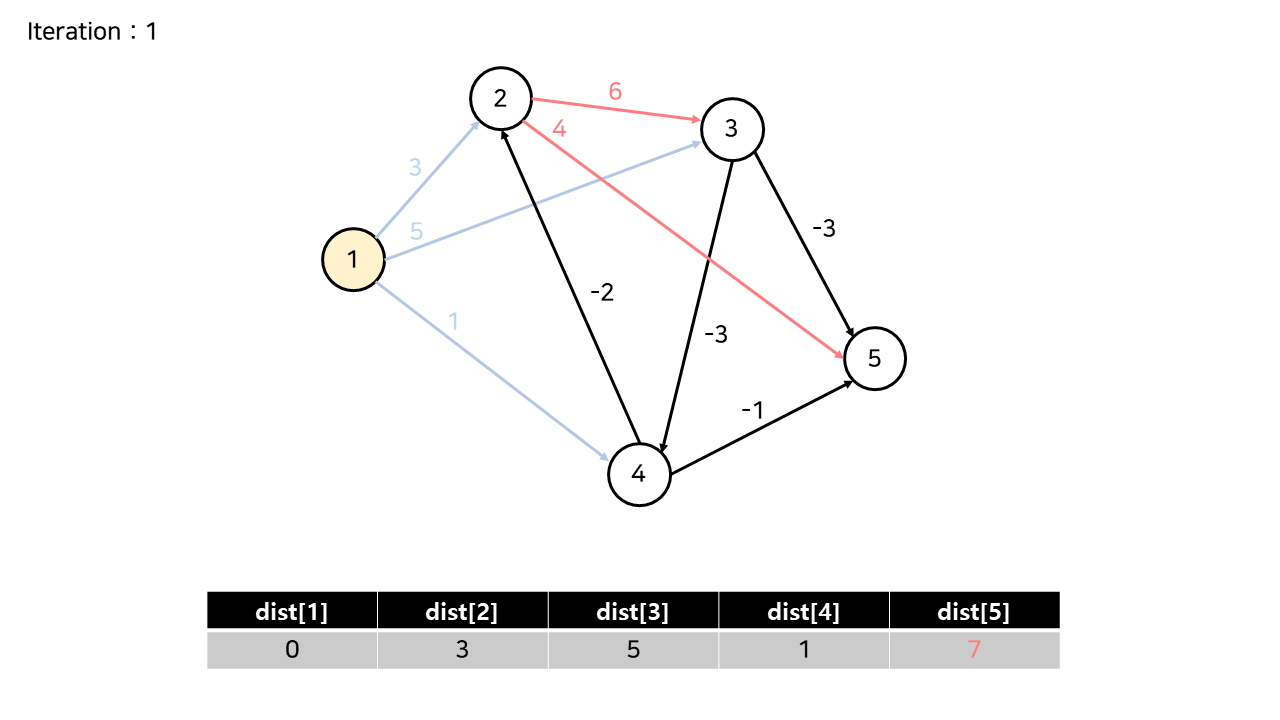
2 => 5 : 7
2 => 3 : 1 => 3번으로 가는게 더 짧기 때문에 유지되었습니다.

(4) 정점 3

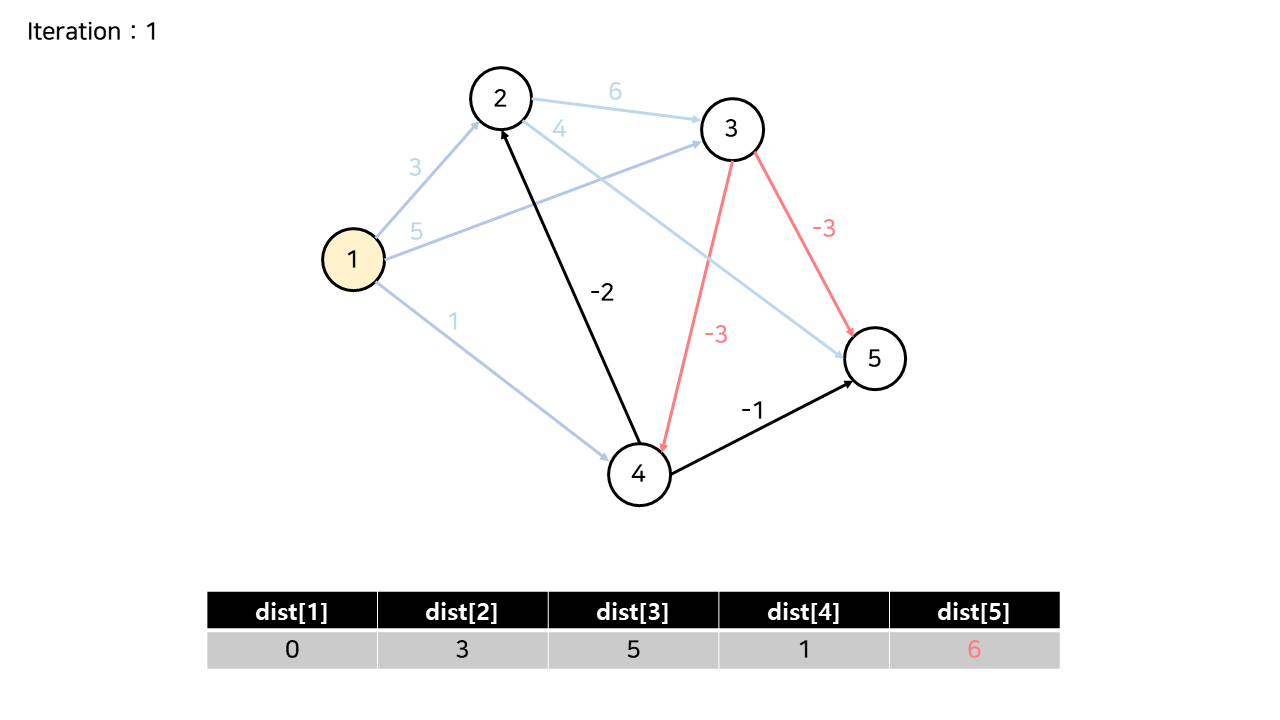
(5) 정점 4

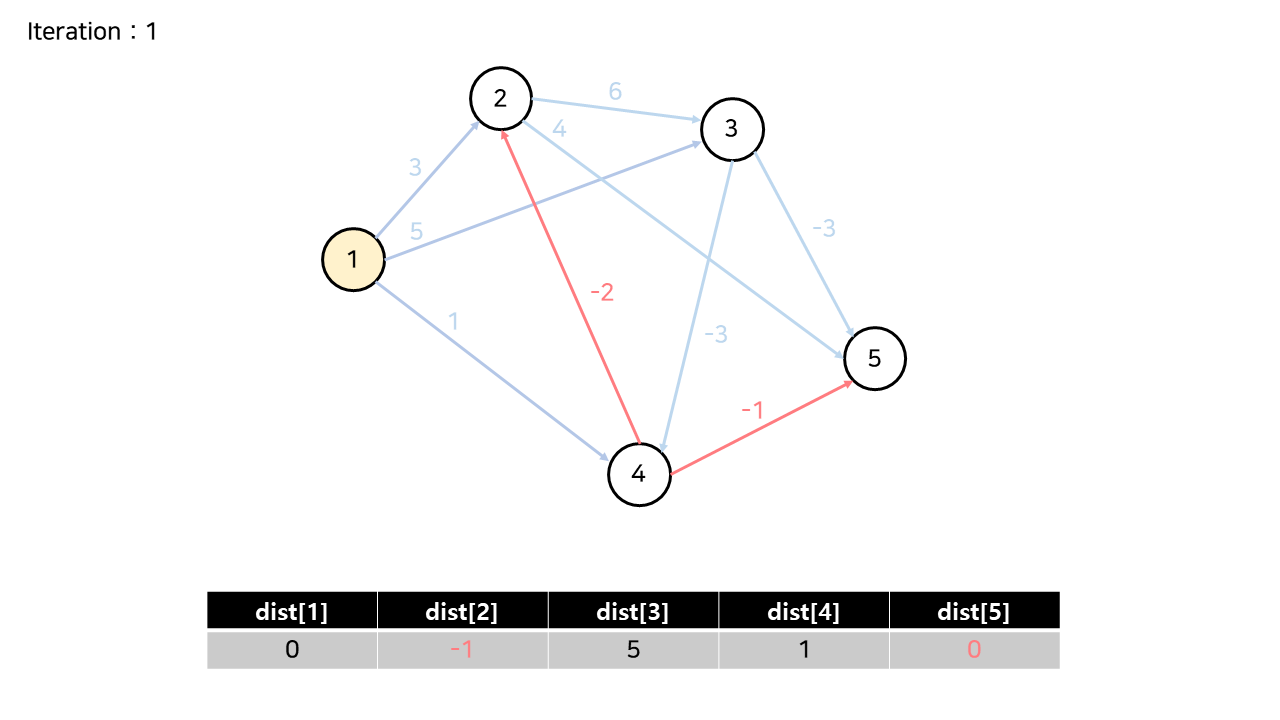
위의 과정을 시작점을 바꿔서 반복합니다.

3. 코드

function BellmanFord(num, edges, start) {
	const INF = Number.MAX_SAFE_INTEGER;
  	const dist = Array(num+1).fill(INF);
  	dist[start] = 0;
  
  for (let v = 1; v <= num -1; v++) {
  	edges.forEach(el => {
    	const [src, dst, weight] = el;
      if (dist[src] !== INF && dist[src] + weight < dist[dst]) {
      	return true;
      }
    })
  }
  const hasNegative = edges.some(el => {
    const [src, dst, weight] = e;
    if (dist[src] !== INF && dist[src] + weight < dist[dst]) {
    	return true
    }
  })
  return hasNegative ? [] : dist.slice(1)
}