플로이드-와샬 알고리즘

Vorhandenheit ·2022년 3월 10일

알고리즘과 자료구조

목록 보기

12/16

플로이드-와샬 알고리즘 (Floyd-Warshall)

다익스트라 알고리즘은 하나의 정점을 출발점으로, 모든 정점까지 최단 경로를 구하는 알고리즘이었습니다. 이번 플로이드-와샬 알고리즘은 각각의 정점을 출발점으로 해서 모든 정점까지 최단 경로를 구하는 알고리즘입니다.

모든 정점에 대한 경로를 계산하기 때문에 거리를 저장할 자료구조는 2차원 배열이 됩니다. 2차원 배열을 이용하여 동적 계획법으로 최적의 값을 계산합니다.

dp [i][j] = min( dp[i][j], dp[i][k] + dp[k][j])
정점 i, j 사이에 모든 경유지를 탐색해서 그 중 최단 경로를 찾아내는 것

시간복잡도

매번 모든 노드들의 조합에 대해서 현재까지 최단 경로를 구하고, 총 N-1번 반복합니다.

O(N^3

1. 동작 원리

(1) 2차원 배열을 만들고 그래프의 간선의 정보를 저장합니다.

(두 정점이 직접적으로 연결되어 있지 않으면 INF(무한대)값, 자기 자신으로 가는 거리는 0으로 합니다.)

(2) 경유지 1 ~ V 까지 순회하여 2차원 테이블을 업데이트 합니다.

2. 설명

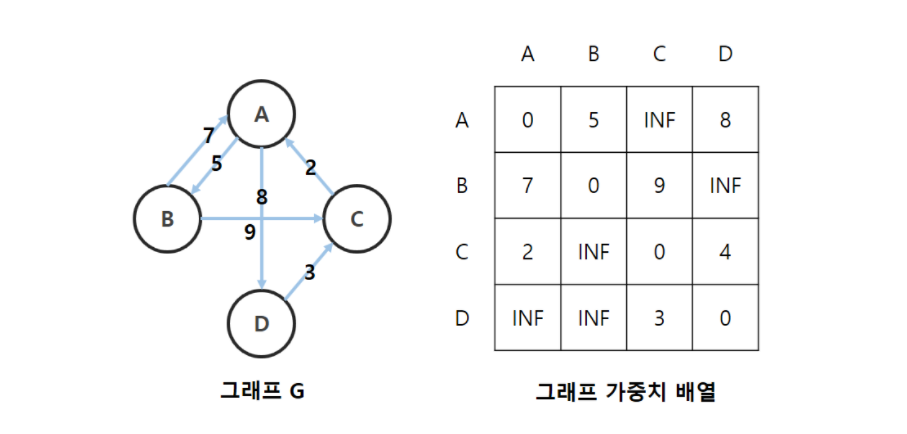
(1) 출발 정점 A

출발 정점을 A로 설정하고, 거쳐야할 정점을 A로 설정했습니다.
A에 인접한 정점은 B, D입니다.
따라서

A => A => B : 이동거리 5
A => A => D : 이동거리 8

(2) 출발 정점 B

출발 정점을 B로 설정하고, 거쳐야할 정점을 B로 설정했습니다.
B에 인접한 정점은 A, C입니다.
따라서

B => A => A : 이동거리 7
C => A => C : 이동거리 INF

(3) 출발 정점 C

출발 정점 C로 설정, 거쳐야할 정점 A로 설정
C에 인접한 정점은 A, D입니다.
따라서

C => A => A : 이동거리 2
C => A => D : 이동거리 10

(4) 출발 정점 D

출발 정점 D로 설정, 거쳐야할 정점 A로 설정
따라서

D => A => C : 이동거리 INF

바로가는 값과 거쳐서가는 값을 모두 다 구해서, 이차원 표로 만들어 최소 값만을 반환합니다

3. 코드

for (let k = 0; k < N; ++k) {
    for (let i = 0; i < N; ++i) {
        for (let j = 0; j < N; ++j) {
            if (d[i][j] > d[i][k] + d[k][j]) {
                d[i][j] = d[i][k] + d[k][j];
            }
        }
    }
}

첫 번째 반복문 k = 1 ~ N: 거쳐가는 정점
두 번째 반복문 i = 1 ~ N: 시작점
세 번째 반복문 j = 1 ~ N: 도착점

d[i][j] = min(d[i][j], dist[i][k] + d[k][j]
i 에서 j로 갈 때, k르 ㄹ거쳐가는 것이 더 가깝다면 대입

function createGraphByList(num, edges) {
	const _edges = {};
  for (let i = 1; i <= num; i++) {
  	_edges[i] = [];
  }
  edges.forEach(([src, dst, weight]) => {
  	_edges[src].push({ node: dst, weight: weight });
  })
  return _edges;
}

function createGraphByMatrix(num edges) {
	const matrix = []';
  	const INF = 101;
  	for (let i = 0; i <= num; i++) {
    	matrix.push(Array(num + 1).fill(INF));
      	matrix[i][i] = 0; // 자기자신은 0
    }
  edges.forEach(([src, dst, weight]) => {
  	matrix[src][dst] = weight;
  })
  return matrix;
}

function FloydWarshall(num, edges) {
	//그래프를 생성
	const dist = createGraphByMatrix(num, edges);
  // dist는 두 접점 간의 최단 거리를 저장하는 인접 행렬입니다.
  // dist[src][dst]는 정점 src로부터 정점 dst까지의 최단거리를 뜻합니다.
  for (let stopover = 1; stopover <= num; stopover++) {
  	for (let src = 1; src <= num; src++) {
    	for (let dst = 1; dst <= num; dst++) {
        	if (dist[src][dst] + dist[stopover][dst] < dist[src][dst]) {
            	dist[src][dst] = dist[src][stopover] + dist[stopover][dst]
            }
        }
    }
  }
  const INF = 101;
  const result = dist.map(row => {
  	row.map(col => {
    	if (col === INF) return null;
      	else return col
    })
  })
  return result.slice(1).map(row => row.slice(1));
}