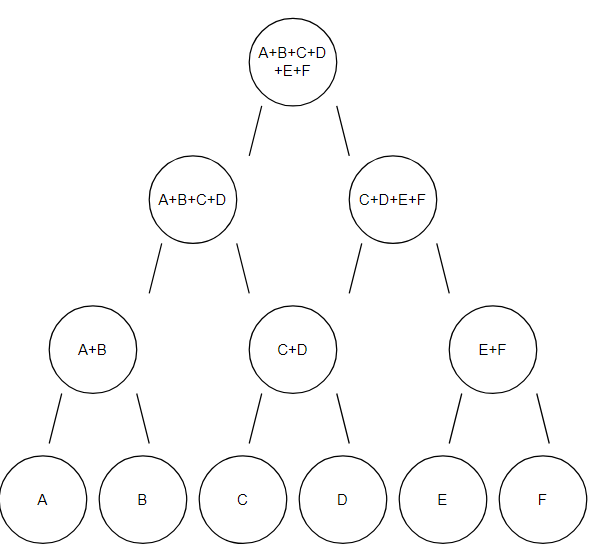
Segment Tree

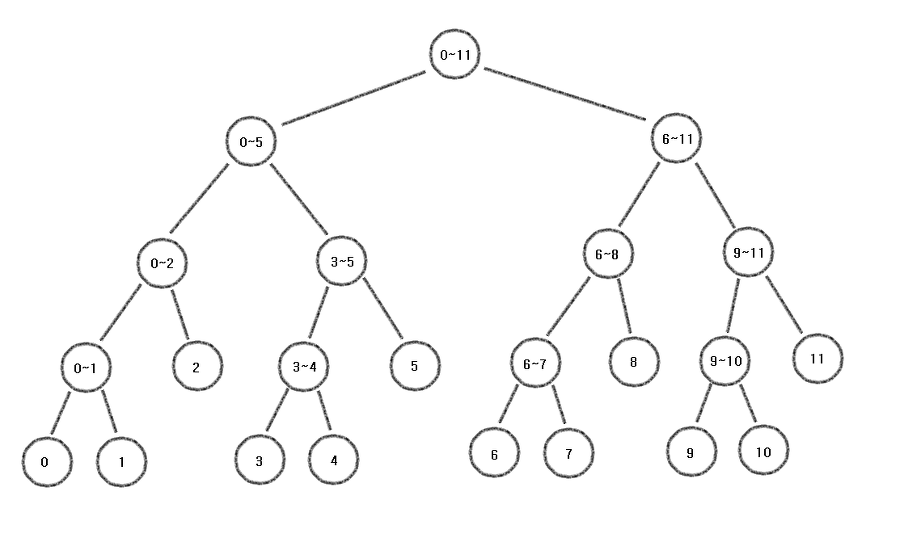
segment tree 혹은 구간 트리라고도 부른다.
보통 구간합으로 예시를 많이 들지만 세그먼트 트리는 주어진 쿼리에 대해 빠르게 응답하기 위해 만들어진 자료구조입니다.

쿼리
주어진 요구사항에 대해 맞는 결과물을 제시

배열에서 어떤 구간의 최솟값이나 합을 찾아야할 때, 간단하게 for문을 통해서 답을 찾을 수 있지만 시간복잡도가 O(N)입니다.
혹시나 배열에 숫자를 바꾸고 M번 수행한다치면 O(MN)의 시간이 걸립니다.

이러한 시간복잡도를 낮추기 위해서 세그먼트 트리를 사용합니다.
세그먼트 트리를 사용할 경우 O(MlongN)걸리게 됩니다.

트리만들기

먼저 최솟값을 구하는 트리를 만들어보겠습니다.

input = [7, 3, 2, 6, 5, 8, 1, 4] 라는 배열이 있을 때

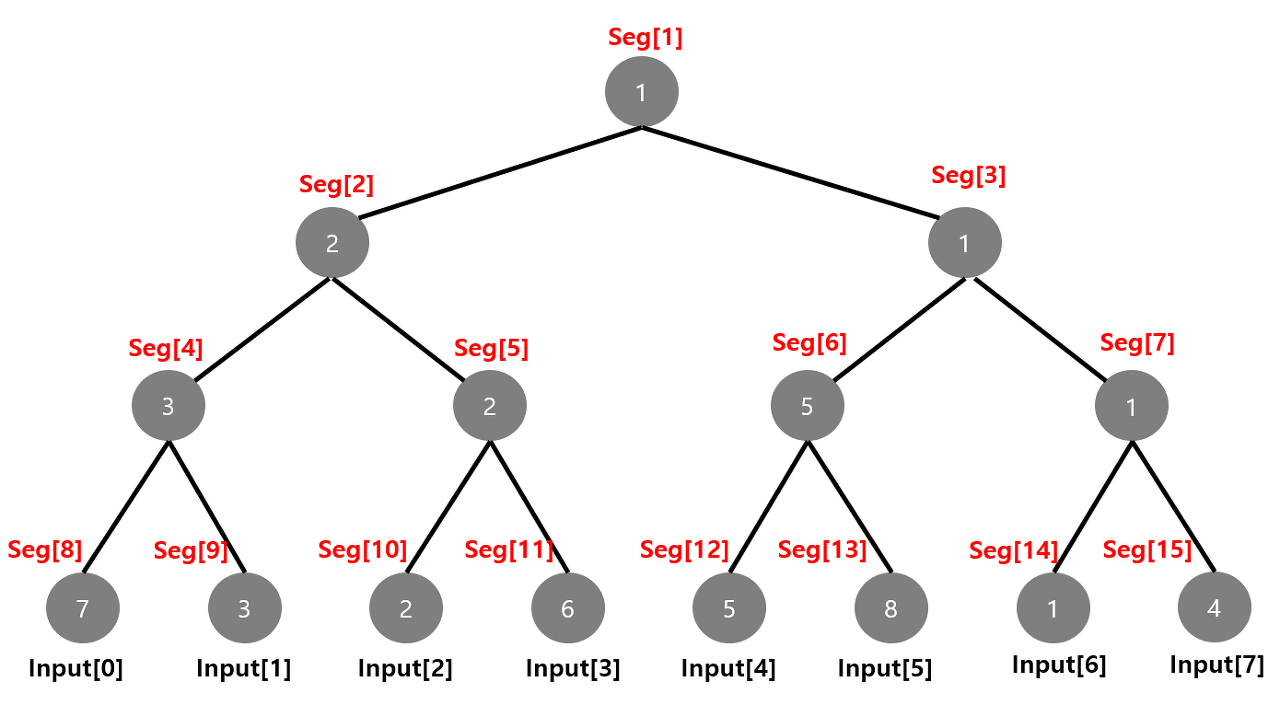
위와같이 트리가 만들어져야할 것입니다.해당 트리가 만들어지면, 구간을 입력하면 해당 최솟값을 출력하기만 하면 됩니다.
binary heap sort와 모습은 비슷하지만 swap의 과정이 없으니 원배열이 바뀌지않습니다. 서로 값을 비교하기만 해서 값을 올리기만 하면 됩니다.

const createTree = (arr, start, end) => {
	if (start === end) {
    	return {value : arr[end]}
    }
  	const mid = Math.floor((start +end) /2); //중간점을 만든다
  	const left = createTree(arr, start, mid)
    const right = createTree(arr, mid+1, end)
    return {
    	value : Math.min(left.value, right.value),
      	left,
      	right
    }
}
const tree = createTree(arr, 0, arr.length-1)

트리가 만들어졌습니다.
각 노드에 최솟값이 적혀있습니다. 노드를 호출하면 최솟값이 반환됩니다.

const findMin = (treeStart, treeEnd, start, end, tree) {
	if (start <= treeStart && treeEnd <= end) { // 트리와 구간이 일치하거나 부분일 경우
    	return tree.value;
    }
  	else if (treeStart > end || start > tree End) { // 겹치지 않을 때
      return
    }
  	// 겹치는 부분이 있을 때
  	const mid = Math.floor((start + end) / 2);
  	return Math.min(
    	findMin(treeStart, mid, start, end, tree.left),
      	findMin(mid+1, treeEnd, start, end, tree.right)
    );
}

const min = ranges.map((range) => {
	const [start, end] = range
    return findMin(0, arr.length -1, start, end, tree)
})

배열

배열을 통해서도 트리 생성이 가능합니다.

const rangeMinimum = function (arr, ranges) {
  const createMinTree = (arr, ts, te, tree, idx) => {
    if (ts === te) {
      tree[idx] = arr[ts];
      return arr[ts];
    }

    const mid = Math.floor((ts + te) / 2);
    tree[idx] = Math.min(
      createMinTree(arr, ts, mid, tree, idx * 2 + 1), //
      createMinTree(arr, mid + 1, te, tree, idx * 2 + 2)
    );

    return tree[idx];
  };

  let tree = [];
  createMinTree(arr, 0, arr.length - 1, tree, 0);

  const findMin = (ts, te, rs, re, idx) => {
    if (rs <= ts && te <= re) {
      return tree[idx];
    }

    if (te < rs || re < ts) {
      return Number.MAX_SAFE_INTEGER;
    }

    const mid = parseInt((ts + te) / 2);
    return Math.min(
      findMin(ts, mid, rs, re, 2 * idx + 1), //
      findMin(mid + 1, te, rs, re, 2 * idx + 2)
    );
  };

  const mins = ranges.map((range) => {
    const [start, end] = range;
    return findMin(0, arr.length - 1, start, end, 0);
  });
  return mins;
};

출처

https://www.crocus.co.kr/648
https://velog.io/@wjdqls9362/Algorithm-%EA%B5%AC%EA%B0%84-%ED%8A%B8%EB%A6%AC-Segment-Tree