Divide and Conquer 2

저번 시간에는 Divide and Conquer의 개념과 그 사례에 대해 함께 알아봤습니다.

이번 시간에는 합병 정렬을 활용한 Divide and Conquer의 사례를 함께 보겠습니다.

⛳ 합병 정렬

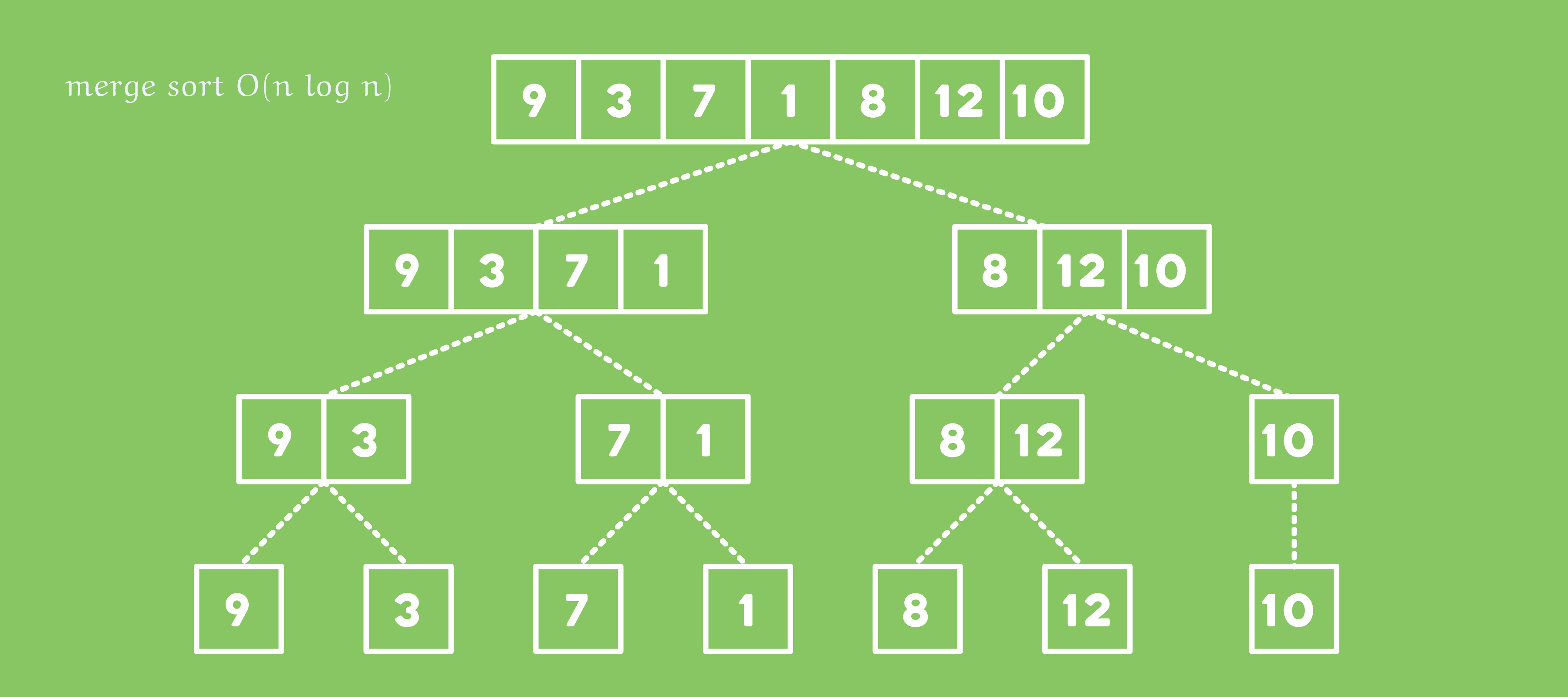
앞서 알고리즘의 기초를 배우는 챕터에서 선택 정렬과 삽입 정렬에 대해 배웠던 것을 기억하시나요? 당시에 정렬에는 그 두 방법 외에도 더 다양한 방법이 있다는 것을 알려 드렸었는데요. 이번 시간에는 그 중 하나인 합병 정렬(Merge Sort)에 대해 함께 알아 봅시다.

지난 시간에 배웠던 Dvide and Conquer의 세 가지 과정을 합병 정렬에 적용하면 다음과 같습니다.

Divide and Conquer
1. Divide: 리스트를 반으로 나누기
2. Conquer: 왼쪽 리스트와 오른쪽 리스트를 각각 정렬하기
3. Combine: 정렬된 두 리스트를 하나의 정렬된 리스트로 합병하기

먼저 Divide 단계에서는 리스트를 왼쪽 반, 오른쪽 반으로 나눕니다. 왼쪽 반을 정렬하는 부분 문제와 오른쪽 반을 정렬하는 부분 문제로 나누어지는 것이죠.

Conquer 단계에서는 두 부분 문제를 각각 정복해야 합니다. 즉, 왼쪽 리스트와 오른쪽 리스트가 각각 정렬되는 것이죠.

Combine 단계에서는 두 리스트를 합쳐 하나의 리스트로 만들어주면 됩니다. 이렇게 하면 기존의 리스트를 정렬한 새로운 리스트가 됩니다.

이렇게만 보면 또 쉽게 느껴지죠? 하지만 우리가 무책임하게 넘어간 부분이 있습니다. 바로 두 리스트를 하나의 리스트로 합쳐주는 Combine 부분인데요.

리스트를 하나로 합칠 때 단순히 합치기만 하면 안 되고 두 리스트의 요소를 비교하여 작은 값부터 차례로 정렬해야 합니다.

예를 들어 왼쪽 리스트의 첫 숫자가 4고 오른쪽 리스트의 첫 숫자가 3이라면 두 리스트를 합칠 때 오른쪽 리스트의 첫번째 요소가 합친 리스트에 첫 요소가 되어야 합니다.

이렇게 두 정렬된 리스트를 하나의 정렬된 리스트로 합병하는 과정을 토대로 합병 정렬이 파생 되었습니다.

⛳ 합병 정렬 진행 과정

이제 합병 정렬의 진행 과정을 자세히 알아봅시다.

[3, 5, 2, 6, 7, 4, 1, 8]

8개의 요소가 담긴 리스트가 있습니다. 이제 이 리스트를 정렬하려고 합니다. Divide and Conquer의 세 단계를 적용해서 풀어봅시다.

먼저 Divide 단계입니다. 리스트를 반씩 나누어주면 되죠?

[3, 5, 2, 6]
[7, 4, 1, 8]

한 번에 풀기에는 아직도 리스트가 좀 큽니다. 따라서 한 번 더 Divide and Conquer를 해야할 것 같습니다.

[3, 5]
[2, 6]

이번에도 한 번에 풀만큼 리스트의 크기가 작지 않으므로 다시 한 번 Divide and Conquer를 해줍시다.

[3]
[5]

이번에는 리스트의 요소가 하나밖에 없기 때문에 이미 정렬되었다고 볼 수 있습니다. 드디어 두 부분 문제를 정복한 거죠.

이제 정복한 두 부분 문제의 답을 활용해 Combine 단계에서 합쳐줘야 합니다. 5보다는 3이 작기 때문에 3, 5의 순서로 정렬되면 됩니다. 그럼 [3, 5]의 부분 문제도 해결된 셈입니다.

다음으로 [2, 6]의 부분 문제를 구해야 합니다.

[2]
[6]

이렇게 되겠죠? 위와 마찬가지로 요소가 하나 밖에 없기 때문에 부분 문제가 정복 되었습니다. 2가 6보다 작으므로 2, 6의 순서로 정렬이 되고 이로써 [2, 6]의 부분 문제가 해결되었습니다.

이제 Combine 단계에서 두 정렬된 리스트를 합쳐야 합니다. 두 리스트의 첫번째 값들만 보면 되는데 왼쪽 리스트의 경우 3이 있고 오른쪽 리스트의 경우 2가 있습니다. 2가 3보다 작으므로 합쳐진 리스트의 첫 요소로 들어갑니다.

다음으로는 3이 제일 작으므로 3을, 그 다음에는 5를, 마지막으로 6을 리스트에 넣어주면 됩니다. 이로써 기존 문제의 왼쪽 반은 완벽하게 정렬 되었습니다. 반대쪽도 마찬가지로 하면 [1, 4, 7, 8]이라는 정렬된 리스트가 됩니다.

마지막으로 Combine 단계에서 두 정렬된 리스트를 합쳐주기만 하면 [1, 2, 3, 4, 5, 6, 7, 8]이라는 정렬된 리스트가 완성 됩니다.

⛳ 합병 정렬 코드

이제 합병 정렬을 코드로 구현해 봅시다.

❗ merge 함수

앞서 정렬된 두 리스트를 하나의 정렬된 리스트로 합병하는 과정으로부터 합병 정렬이 파생 되었다고 했죠? 따라서, 합병 정렬 함수를 작성하기 전에 이 과정을 수행하는 함수 merge부터 작성해보도록 하죠.

merge 함수는 정렬된 두 리스트 list1과 list2를 파라미터로 받고 하나의 정렬된 리스트를 반환합니다.

def merge(list1, list2):

먼저, 정렬된 요소들이 담길 merge_list를 만들어 줍시다.

merge_list = []

다음으로 해야할 것은 list1과 list2를 도는 각각의 인덱스를 설정하는 일입니다. while문으로 작성할 것이므로 각 인덱스는 0으로 초기화 해야 합니다.

i = 0
j = 0

이제 반복문을 돌 차례입니다. list1과 list2를 돌며 각 리스트의 요소를 서로 비교한 후, 더 작은 값을 merge_list에 넣어야 합니다. 그 뒤에는 더 작은 요소를 가진 리스트의 인덱스가 1 증가합니다.

이때, while문의 조건 부분에는 인덱스의 값이 두 리스트의 크기보다 커지기 전까지만 돌도록 설정해줘야 합니다.

while i < len(list1) and j < len(list2):
    if list1[i] > list2[j]:
        merge_list.append(list2[j])
        j += 1
    else:
        merge_list.append(list1[i])
        i += 1

앞서 while문의 조건 부분에 작성했던 내용은 두 리스트 중 어느 하나라도 요소가 모두 소진될 경우 프로그램을 종료한다는 뜻을 내포하고 있습니다.

따라서, 다음으로 해야 될 작업은 두 리스트 중 소진된 리스트와 소진되지 않은 리스트가 무엇인지 판별하고 소진되지 않은 리스트를 위 반복문의 결과와 연결하는 일입니다.

이는 인덱스를 활용해서 표현할 수 있습니다. 만약 인덱스 i가 list1의 크기와 같아진다면 이는 list1이 소진되었음을 의미합니다. 이때, 소진되지 않은 나머지 list2의 요소들은 merge_list에 추가되어야 합니다.

리스트와 문자열은 '+' 연산자를 활용해서 연결할 수 있었죠?

if i == len(list1):
    merge_list += list2[j:]
elif j == len(list2):
    merge_list += list1[i:]

리스트 슬라이싱의 범위 지정에 대해 이해가 안 되시는 분들을 위해 첨언하자면, 상대 인덱스가 증가하는 동안에는 해당 인덱스의 크기는 커지지 않고 동일한 값을 유지합니다. 상대 인덱스가 리스트의 크기만큼 증가하고 나서야 비로소 나머지 인덱스가 멈춘 지점부터 남은 요소들을 반환하기 위해 [i:], [j:] 형태가 된 것입니다.

merge 함수가 받는 리스트 파라미터는 이미 정렬이 된 상태이기 때문에 따로 정렬할 필요 없이 리스트 슬라이싱으로 값을 불러오면 된다는 것을 잊지 마세요.

이제 전체 코드와 예시를 봅시다.

def merge(list1, list2):
    
    merge_list= []

    i = 0
    j = 0

    while i < len(list1) and j < len(list2):
        if list1[i] > list2[j]:
            merge_list.append(list2[j])
            j += 1
        else:
            merge_list.append(list1[i])
            i += 1

    if i == len(list1):
        merge_list += list2[j:]
    elif j == len(list2):
        merge_list += list1[i:]

    return merge_list

print(merge([1],[]))
print(merge([4],[2]))
print(merge([5, 6, 7, 8],[1, 2, 3, 4]))

[1]
[2, 4]
[1, 2, 3, 4, 5, 6, 7, 8]

❗ 합병 정렬

이제 합병 정렬 함수를 작성할 차례입니다.

merge_sort는 파라미터로 리스트 하나를 받고 정렬된 새로운 리스트를 반환하는 함수입니다. Divide and Conquer 방식으로 함수를 작성해봅시다.

우선 base case를 설정해야 합니다. 합병 정렬 문제를 단번에 풀 수 있는 경우는 언제인가요? 바로 리스트의 크기가 0과 1일 때입니다. 이 때는 이미 정렬된 상태이기 때문에 리스트를 그대로 반환하면 되기 때문이죠.

if len(my_list) < 2:
    return my_list

다음으로 Divide and Conquer의 세 가지 과정을 짚어 봅시다.

1. Divide: 리스트 슬라이싱을 통해 리스트 반씩 나누기
2. Conquer: 왼쪽 반과 오른쪽 반을 각각 merge_sort 함수로 정렬하기
3. Combine: 정렬된 두 리스트를 merge 함수로 합치기

리스트를 반으로 나누기 위해 리스트 크기의 중간값을 변수로 선언해줍니다.

mid = len(my_list)//2

이제 Conquer와 Combine 단계를 한꺼번에 작성해줍니다. 이때, merge와 merge_sort의 쓰임을 헷갈리지 않도록 주의해주세요.

merge는 파라미터 두 개가 필요하고 merge_sort는 파라미터 한 개가 필요합니다. merge의 역할은 나눠진 두 리스트의 요소를 비교하여 정렬하는 것이고 merge_sort의 역할은 하나의 리스트를 두 부분으로 나눈 후 정렬하는 것입니다.

참고로 이 부분은 재귀 함수의 recursive case와 같습니다.

return merge(merge_sort(my_list[:mid]), merge_sort(my_list[mid:]))

이제 전체 코드와 예시를 봅시다.

def merge_sort(my_list):

    if len(my_list) < 2:
        return my_list
        
    mid = len(my_list)//2
    return merge(merge_sort(my_list[:mid]), merge_sort(my_list[mid:]))

print(merge_sort([2, 4, 6, 8, 1, 3, 5, 7]))
print(merge_sort([26, 11, 7, 28, 3, 46, 7, 11, 17]))

[1, 2, 3, 4, 5, 6, 7, 8]
[3, 7, 7, 11, 11, 17, 26, 28, 46]

---

이번 시간에는 Divide and Conquer 방식으로 합병 정렬의 함수를 작성해봤습니다. 나누고 정복하고 합치기. 이 과정들이 익숙하신가요?

아직 익숙하지 않아도 괜찮습니다. 또 한 번의 시간이 남아있거든요. 다음 시간에는 이번 시간에 이어 퀵 정렬을 Divide and Conquer 방식으로 구현해보려 합니다. 잘 따라와 주세요 :)

* 이 자료는 CODEIT의 '알고리즘의 정석' 강의를 기반으로 작성되었습니다.