저번 시간에는 알고리즘 패러다임의 첫 시작, Brute Force에 대해 배웠습니다. 모든 경우의 수를 찾는 방식을 활용하고 있어 가장 쉽게 생각해볼 수 있는 접근법이었는데요.
이번 시간에 배울 새로운 알고리즘 패러다임은 Divide and Conquer입니다. Divide and Conquer는 알고리즘 패러다임 중 가장 널리 알려진 방식이기도 합니다. 어떤 접근법인지 함께 알아볼까요?
🚩 Divide and Conquer

Divide and Conquer, 우리말로는 분할 정복이라는 개념에 대해 설명하기 전에 주의 사항이 있습니다. 바로 재귀 개념에 대해 정확한 이해가 있어야 한다는 점인데요.
따라서, 만약 재귀 개념이 제대로 이해가 되지 않았다면 재귀 파트로 돌아가 복습을 하고 오시길 권장 드립니다.
재귀 함수가 어려웠듯 Divide and Conquer 또한 우리가 접할 알고리즘 패러다임 중 가장 어려운 개념이 아닐까 싶습니다.
하지만 재귀 함수 때와 마찬가지로 모두가 어려워하는 개념이기 때문에 너무 겁 먹지 마시고 차근히 잘 따라오다 보면 어느새 이해가 되는 것을 느낄 수 있게 되리라 확신합니다.
오히려 이 개념을 배우고 나면 앞으로 접하게 될 다른 알고리즘 패러다임이 쉽게 느껴질 수도 있습니다.
이제 본격적으로 Divide and Conquer 개념에 대해 알아봅시다. 재귀 함수에서 하나의 큰 문제를 다루는 법에 대해 알아봤었죠? 바로 풀기 어려운 큰 문제는 부분 문제들로 나누어 풀 수 있습니다. Divide and Conquer도 마찬가지입니다.
기존 문제와 같은 형태를 지닌 부분 문제를 활용해서 큰 문제를 해결하는 것이 바로 Divide and Conquer입니다. 각 부분 문제를 풀고 부분 문제들로부터 도출된 답을 활용하여 큰 문제를 풀면 됩니다.
좀 더 구조적인 방식으로 Divide and Conquer에 대해 설명 드리겠습니다. 파라미터 x를 받는 함수 f를 예시로 들겠습니다. 이 함수는 한 번에 풀기엔 너무 커서 부분 문제로 나누어 풀어야 합니다. 이때, 세 가지 과정이 필요한데요.
Divide and Conquer
1. Divide: 문제를 부분 문제로 나누기
2. Conquer: 각 부분 문제를 정복하기
3. Combine: 부분 문제들의 답을 합쳐 기존 문제 해결하기
첫 번째 Divide 단계에서는 인풋 x를 나눕니다. 예를 들어 x1, x2 이런 식으로 말이죠.
그 다음 Conquer 단계에서는 부분 문제를 해결하기 위해 f(x1)과 f(x2)를 합니다. 이렇게 하면 각각 A라는 답과 B라는 답을 얻어낼 수 있습니다. Conquer는 우리말로 정복을 뜻하는데 부분 문제를 푼다는 표현을 부분 문제를 정복한다는 표현으로 바꾸면 이해하기 쉬우실 겁니다.
마지막으로 Combine 단계에서는 부분 문제들로부터 얻어낸 답 A와 B를 활용해서 f(x)를 계산하면 됩니다. 그럼 f(x)의 답인 S를 구할 수 있는 것이죠.
이렇게만 보면 그리 어려워 보이지 않습니다. 그럼에도 왜 Divide and Conquer가 어려운 방식이라고 하는 걸까요?
사실 Conquer 단계가 앞서 본 사례처럼 쉽지만은 않습니다. 실제 동작하는 방식을 봤을 때, 부분 문제인 f(x)와 f(y) 또한 한 번에 풀기 어려운 큰 문제라면 f(x)와 마찬가지로 또 한 번 Divide and Conquer 방식을 적용해야 합니다.
이 말은 즉, 문제가 충분히 작아질 때까지 반복해서 Divide and Conquer을 활용해야 한다는 것인데요. 내부적으로 이렇게 복잡한 작업이 이루어진다는 점에서 Divide and Conquer 방식이 어렵다고 하는 것이죠.
그러나 연습을 거듭하다 보면 나중에는 이 복잡한 과정에 대한 생각을 할 필요 없이 Divide, Conquer, Combine 이 세 가지 과정에만 초점을 두고 문제를 해결할 수 있는 때가 옵니다.
🚩 Divide and Conquer 예시
1부터 100까지 더하는 문제를 Divide and Conquer 방식으로 풀어봅시다. 앞서 배운 Divide, Conquer, Combin 이 세 가지 과정을 떠올리며 문제를 풀면 됩니다.
Divide 단계부터 시작합시다. 1부터 100까지 더하는 문제의 부분 문제는 무엇일까요? 1부터 50까지의 합과 51부터 100까지의 합을 구하는 부분 문제로 나눠볼 수 있습니다. 기존 문제와 동일하지만 크기만 작아진 형태입니다.
다음으로 Conquer 단계입니다. 이 단계에서는 두 부분 문제의 답을 각각 구하면 됩니다. 1부터 50의 합은 1275, 51부터 100의 합은 3775입니다.
이제 마지막 Combine 단계에서 부분 문제들의 답을 더하면 5050이란 값을 구할 수 있습니다. 이는 기존 문제인 1부터 100까지의 합과 동일한 값입니다.
어떤가요? 이해하기 어렵지 않죠? 그렇다면 이번에는 이 연산의 내부 동작을 함께 봅시다. 1부터 100은 너무 크니 1부터 8까지의 합의 사례를 보도록 하죠.
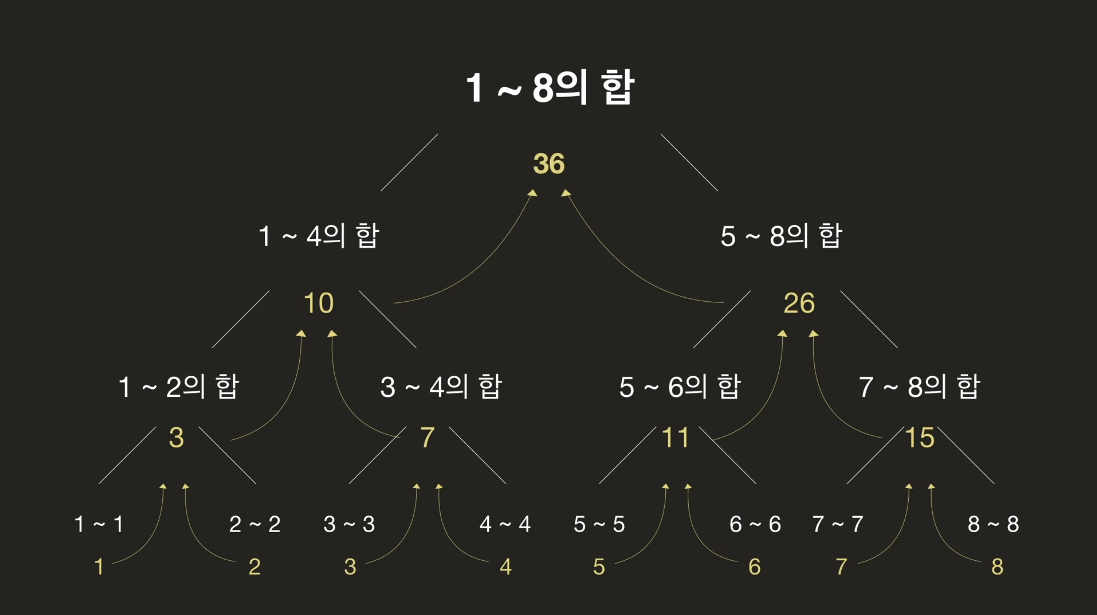
1부터 8까지의 합을 구하는 문제의 부분 문제는 1부터 4까지의 합과 5부터 8까지의 합입니다. 그리고 이 두 부분 문제를 풀기 위해서는 또 다른 부분 문제가 필요하죠. 즉, 재귀적으로 Divide and Conquer를 하는 겁니다.
따라서, 1부터 4까지의 합은 다시 1부터 2까지의 합과 3부터 4까지의 합으로, 5부터 8까지의 합은 다시 5부터 6까지의 합과 7부터 8까지의 합으로 나눌 수 있습니다.
심지어 1부터 2까지 구하는 문제마저도 부분 문제를 구할 수 있는데요. 바로 1부터 1까지의 합과 2부터 2까지의 합으로 말이죠. 이 두 문제는 값이 바로 나오기 때문에 더 이상 부분 문제를 구할 필요가 없습니다.
이 과정까지 내려오고 나서야 Combine 단계로 넘어갈 수 있습니다. 앞서 재귀 함수 챕터에서 더 이상 나눌 수 없는 작은 문제를 base case라고 했었죠? Divide and Conquer에서도 마찬가지입니다.
base case에 도달하고 나서야 두 부분 문제의 합을 더해나가며 기존 문제의 답을 구하게 됩니다.
1부터 2까지의 합을 구하면 3부터 4까지의 합을 구하는 문제를 Divide and Conquer하여 base case의 답을 구하면 됩니다.
이렇게 오른쪽 부분인 5부터 8까지의 합을 구하는 문제도 base case에 도달할 때까지 Divide and Conquer를 반복해야 합니다.
두 부분 문제가 완전히 풀리면 그 답들을 더하여 기존 문제인 1부터 8까지의 합을 구할 수 있게 됩니다.
🚩 1부터 n까지의 합
위 사례를 코드로 구현해 봅시다.
함수 consecutive_sum은 두 개의 정수 start와 end를 파라미터로 받고 start부터 end까지의 합을 반환합니다. 이때, end는 start보다 큰 수입니다.
base case와 부분 문제를 활용하는 만큼 Divide and Conquer 방식의 풀이법은 재귀 함수 풀이법과 매우 유사합니다. 따라서, 재귀 함수를 작성했을 때와 같이 우선 base case부터 구해보도록 하죠.
1부터 n까지의 합을 구하는 문제에서 생각할 필요 없이 가장 쉽게 구할 수 있는 답은 무엇일까요? 위 사례를 보면 알 수 있듯 1과 2의 합을 나누어 1부터 1까지의 합, 2부터 2까지의 합을 구하면 각각 1과 2라는 답이 바로 도출되기 때문에 더 이상 부분 문제로 나눌 필요 없는 base case라고 할 수 있습니다.
이를 코드로 나타내면 다음과 같습니다.
if start == end:
return start1부터 1까지의 합, 2부터 2까지의 합은 start와 end 두 값이 같은 경우라고 할 수 있습니다. 따라서, 이 두 값이 같을 때는 start 값을 반환해줍니다.
다음으로 Conqure 단계에 들어갑시다. 재귀 함수로는 recursive case를 구하는 단계가 되겠네요.
재귀 함수에서 연산에 관한 recursive case를 구할 때 수식의 일반화를 떠올리면 쉽다고 배웠습니다. 1부터 100까지의 합을 1부터 50까지의 합으로 구하기 위해서는 어떤 과정이 필요할까요?
50과 51이라는 수는 100의 중간값인 50으로부터 구할 수 있습니다. 즉, 100의 중간값을 구해야 합니다. 이 중간값은 왼쪽 case의 end 값이 되고 오른쪽 case에서는 1이 더해진 후 end 값이 됩니다.
이를 수식으로 일반화 해봅시다. 중간값은 수식으로 어떻게 표현할 수 있을까요? start와 end를 더하고 이를 2로 나누면 됩니다.
middle = (start+end) // 2따라서, recursive case는 다음과 같이 나타낼 수 있습니다.
return consecutive_sum(start, middle) + consecutive_sum(middle+1, end)이제 전체 코드와 예시를 봅시다.
def consecutive_sum(start, end):
if start == end:
return start
mid = (start + end) // 2
return consecutive_sum(start, mid) + consecutive_sum(mid + 1, end)
print(consecutive_sum(1, 10))
print(consecutive_sum(1, 100))55
5050이번 시간에는 하나의 거대한 문제를 부분 문제로 나누어 정복하는 Divide and Conquer 방식을 배웠습니다. Divide and Conquer와 재귀 함수는 매우 유사하기 때문에 만약 재귀 함수를 완벽히 이해했다면 이번 시간이 마냥 힘들지만은 않았을 것 같습니다.
다음 시간에는 이번 시간에 이어 Divide and Conquer의 더 다양한 사례들을 함께 보겠습니다.
* 이 자료는 CODEIT의 '알고리즘의 정석'을 기반으로 작성되었습니다.