[PRML정리]1.1 예시:다항식 곡선 피팅

임용택·2021년 4월 16일
PRML-chapter1prml
0

PRML

목록 보기
1/3
post-thumbnail

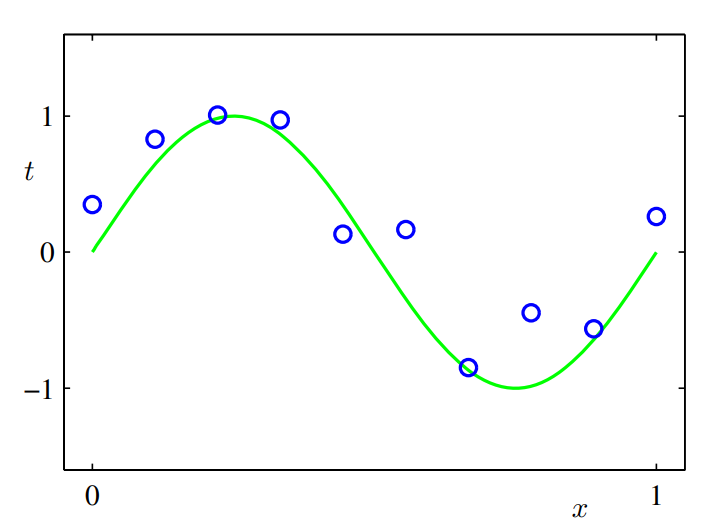
1장에선 sin(2πx)sin(2\pi x)함수를 베이스로 타겟 변수에는 약간의 랜덤한 노이즈를 포함시켜 데이터를 만들어 다양한 컨셉에 대해 설명할 것.

  • N 개의 관찰값 xx로 이루어진 훈련 집합 x = (x1,...,xN)T(x_{1},...,x_{N})^{T}, 그리고 target t = (t1,...,tN)T(t_{1}, ..., t_{N})^{T}가 있다고 하자.
  • N=10인 경우에 대해 우선 이야기 해보자.
  • 입력 데이터 잡힙 x 는 서로 간에 같은 거리를 두고 균등하게 xnx_{n} 값을 선택하여 만듦.
  • target 변수 t의 값 tnt_{n}(n = 1, ..., N)은 sin(2πx)sin(2\pi x)에 가우시안 분포를 따르는 노이즈를 더해 만듦.

목표는 훈련 집합을 사용하여 입력값 x^\hat{x}가 주어졌을 때 target 변수 t^\hat{t}를 예측하는 것.
이는
1. 한정된 데이터로부터 일반화를 시행해야 해서,
2. 관측된 값들은 높은 확률로 노이즈를 포함하여 x^\hat{x}에 대응되는 적합한 t^\hat{t}를 찾기 힘들어서
어려운 문제이다.

1.2절에서는 확률론을 이용해 불확실성을 정량적으로 표현하고, 1.5절에서는 의사 결정 이론을 통해 최적의 예측을 하는 데에 있어 확률적인 표현을 활용하는 법을 공부한다.
그에 앞서, 약식으로 진행해보자.

위의 곡선을 피팅하기 위해 아래의 다항식을 사용한다.

y(x,w)=w0+w1x+w2x2+...+w0=∑j=0Mwjxjy(x, w) = w_{0} + w_{1}x + w_{2}x^{2} +...+w_{0}=\sum_{j=0}^{M}w_{j}x^{j}

M은 다항식의 차수이고, w0,w1,...,wMw_{0}, w_{1}, ..., w_{M}을 모아 벡터 w로 표현 가능하다.

다항 함수 y(x,w)y(x, w)는 xx에 대해서는 비선형이지만 계수 w에 대해서는 선형이다.
-> 직관적으로 와닿지 않는데, 정리되면 내용 추가함.

다항 함수와 같이 알려지지 않은 변수에 대해 선형인 함수들은 중요한 성질을 지녔으며, 선형 모델이라 불린다. 이는 3,4 장에서 배울 것!

다항식을 train dataset에 피팅하여 계수 w의 값들을 정할 수 있다.

trainset의 target과 y(xy(x,w)의 오차를 측정하는 error function을 정의하고, 이 값을 최소화 하는 방식으로.
가장 널리 쓰이는 간단한 오차 함수 중 하나는 아래와 같다.
EE(w)=12∑n=1N{y(xn,w)−tn}2\frac{1}{2}\sum^{N}_{n=1}\{y(x_{n},\boldsymbol{w})-t_{n}\}^{2}

위의 함수의 결과값은 항상 양수이고, n=1,2,...,Nn=1,2,...,N 에 대해 y(xn,w)y(x_{n},\boldsymbol{w}) 과 tnt_{n}이 모두 일치할 때만 그 값이 0이 된다는 사실을 알아두자.

E(w)E(\boldsymbol{w})을 최소화하는 w를 선택하여 곡선 피팅 문제를 해결할 수 있는데, 오차 함수를 계수에 대해 미분하면 w에 선형적인 식이 나올 것이므로 위의 오차함수를 최소화하는 유일한 w인 w∗\boldsymbol{w}^{*}를 찾아낼 수 있을 것이다.
결과에 해당하는 다항식은 함수 y(x,w∗)y(x, \boldsymbol{w}^{*}) 의 형태를 보일 것.

다항식의 차수 M을 결정하는 것도 문제다.

이런 문제를 모델 비교(model comparison), 모델 결정(model selection)이라 함.
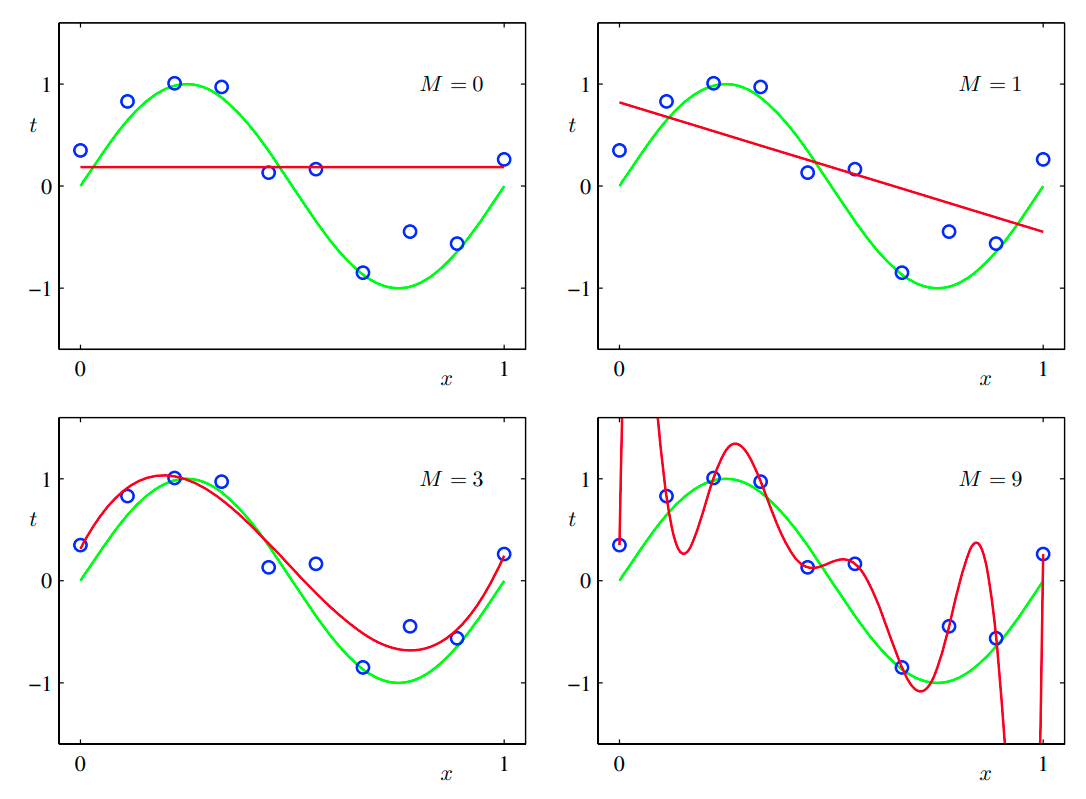
아래 그림에서는 M = 0, 1, 3, 9인 경우에 대해 예시를 보여준다.

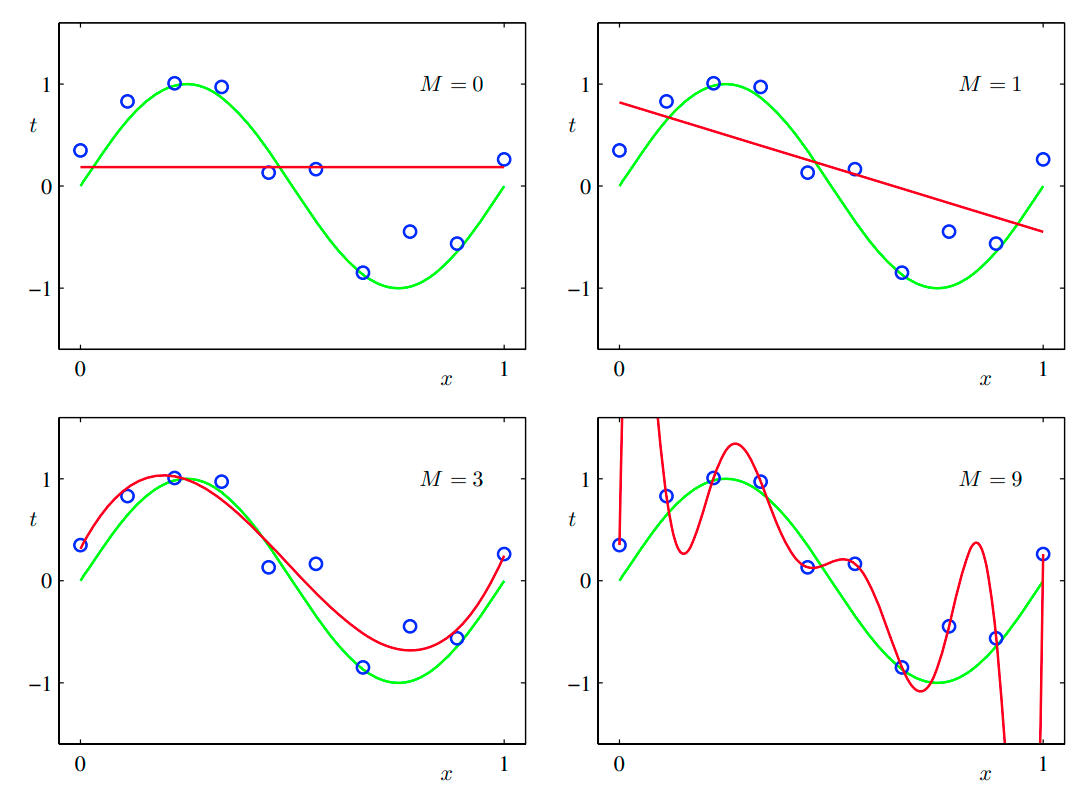
M = 0, M = 1 의 경우 거의 피팅을 못 한 것을 확인할 수 있는데, 이러한 경우가 under-fitting의 예시이고,
M = 9의 경우처럼 다항식이 모든 데이터 포인트를 지나 E(w∗)=0E(\boldsymbol{w}^{*}) = 0 인 경우 원래의 함수를 표현하는 데에 실패하는 경우가 over-fitting의 예시이다.

그렇다면 모델 결정은 어떻게?

위에서 보았듯이 피팅의 목표는 새로운 데이터에 대해 정확한 결과값을 예측할 수 있는 일반화의 달성이다.

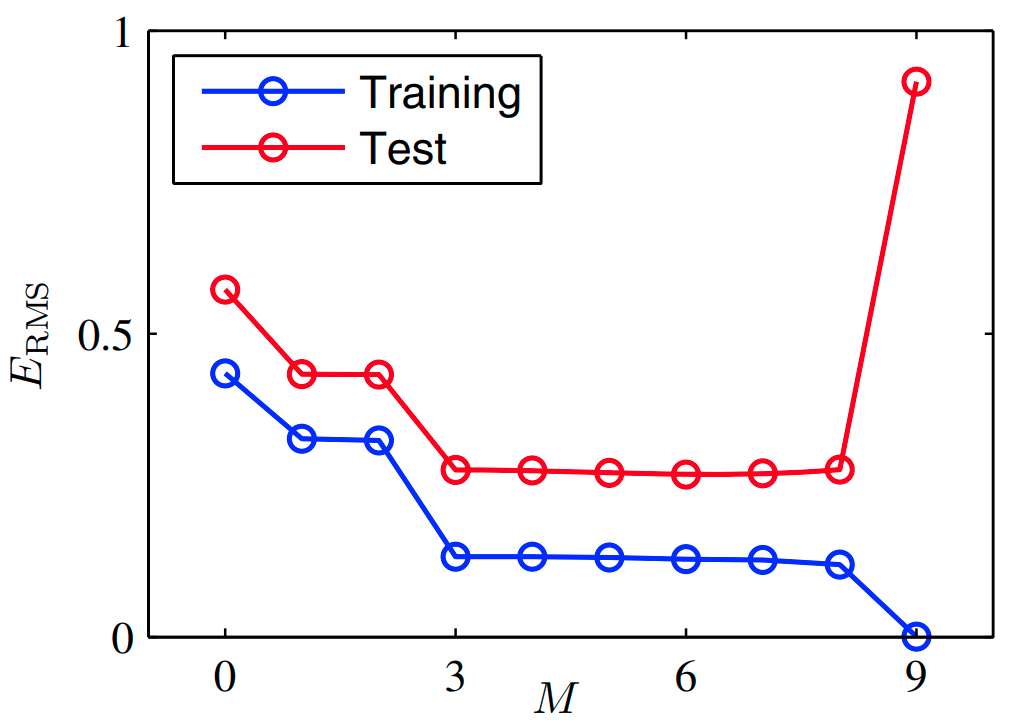
앞서 trainset을 만드는 과정에서 노이즈값만 다르게 적용해 100개의 포인트로 이루어진 testset을 만들었다.
testset에 대해 M의 값에 따라 일반화의 성능이 어떻게 변하는지 정량적으로 살펴볼 수 있다.

차수 M과 계수의 값의 관계?

위의 실험에서 M = 9일 경우 trainset에 대한 오차가 0인 것을 확인할 수 있었다.
이는 당연한 결과인데 그 이유는 10개의 계수를 가지고 10개의 포인트를 피팅해야 하기 때문.
(10개의 변수로 이루어진, 10개의 식을 가진 연립 방정식을 푸는 것과 같은 이치)
하지만 이 경우 함수 y(x,w∗)y(x, \boldsymbol{w}^{*})이 크게 진동하는 것을 확인할 수 있었다.

그런데, 이거 좀 이상하지 않아?
그렇다. 뭔가 이상하다.
3차 다항식은 9차 다항식에서 4차~9차의 계수가 0인 경우인데..
M=9인 다항식은 M=3인 다항식의 결과를 모두 만들어낼 수 있는데..
심지어 sin(2πx)sin(2\pi x)를 급수 전개하면 모든 차수의 항을 다 가지고 있는데..

그럼 당연히 M이 증가함에 따라 단조 증가해야 맞는 거 아닌가?

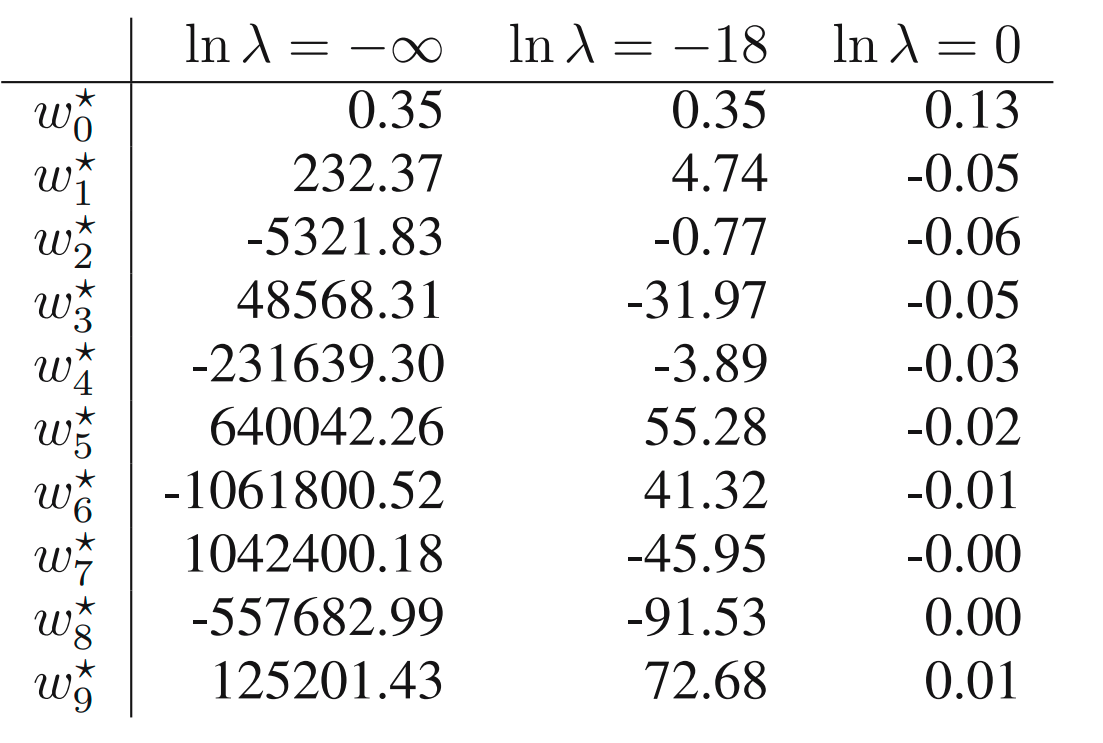
위 표를 보면 알 수 있는데, M이 커지면 계수가 커지는 것 또한 확인할 수 있다.
특히 M = 9의 경우, 그 값이 매우 크고 음/양이 번갈아 나타나는 것을 확인할 수 있는데, 이는 각각의 데이터 포인트에 정확하게 맞도록 피팅한 결과이다.
더 큰 M 값을 가진 다항식이 target 값에 포함된 노이즈에 정확히 피팅되어 나타난 결과.

그럼 노이즈 없으면 M이 클수록 좋겠네?
아마 그런 경우는 없지 않을까..

데이터셋의 크기가 미치는 영향?

사용되는 dataset의 크기가 달라지는 경우는 어떤 일이 일어날까?

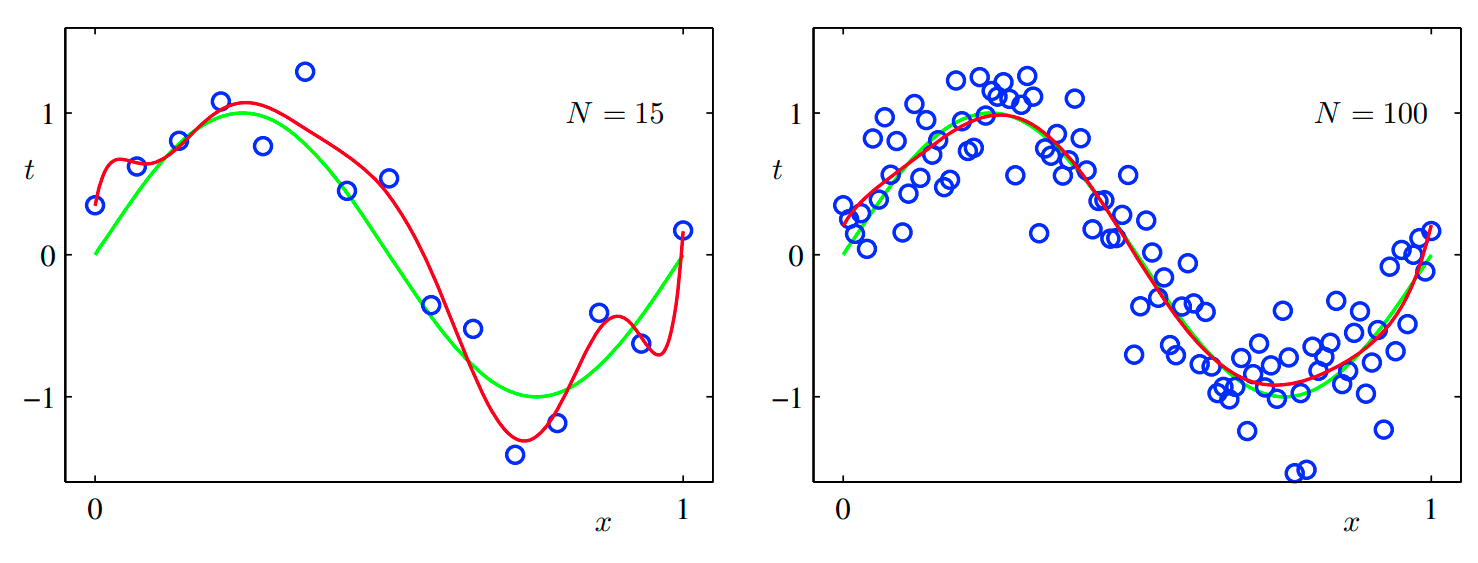
위의 그림을 보면 trainset의 크기가 늘어날수록 over-fitting 문제가 완화되는 것을 볼 수 있다.
이를 달리 표현하면 데이터 집합의 수가 클수록 더 복잡한 모델을 활용하여 피팅할 수 있게 된다는 의미도 된다.

사용 가능한 훈련 집합의 데이터의 수에 따라 모델에서 사용하는 매개변수의 숫자에 제약을 두는 것은 이상하다. 그보다는 풀고자 하는 문제의 복잡도에 따라 모델의 복잡도를 결정하는 것이 더 논리적일 것이다.

앞서 제시한 최소 제곱법은 1.2.5에서 제시한 최대 가능도 방법의 특별한 사례.
베이지안 방법론을 사용하면 과적합 문제를 피할 수 있다. 이 경우 trainset의 크기에 따라 적합한 매개변수의 수가 자동으로 정해짐.

그렇다면, 비교적 유연하고 복잡한 모델을 제한적인 숫자의 trainset에 피팅하려면 어떻게 해야 할까?

정규화?

정규화란 오차함수에 계수의 크기가 커지는 것을 막기 위해 페널티항을 추가하는 것.
이 중 가장 간단한 형태는 각각의 계수를 제곱하여 더하는 것.
정규화를 위한 페널티항을 추가한 오차 함수는 아래와 같다.
E(w)=12∑n=1N{y(xn,w)−tn}2+λ2∣w∣2E(\boldsymbol{w})=\frac{1}{2}\sum_{n=1}^{N}\{y(x_{n}, \boldsymbol{w})-t_{n}\}^{2}+\frac{\lambda}{2}|\boldsymbol{w}|^{2}

계수 λ\lambda가 정규화항의 제곱합 오류항에 대한 중요도를 결정 짓는다.

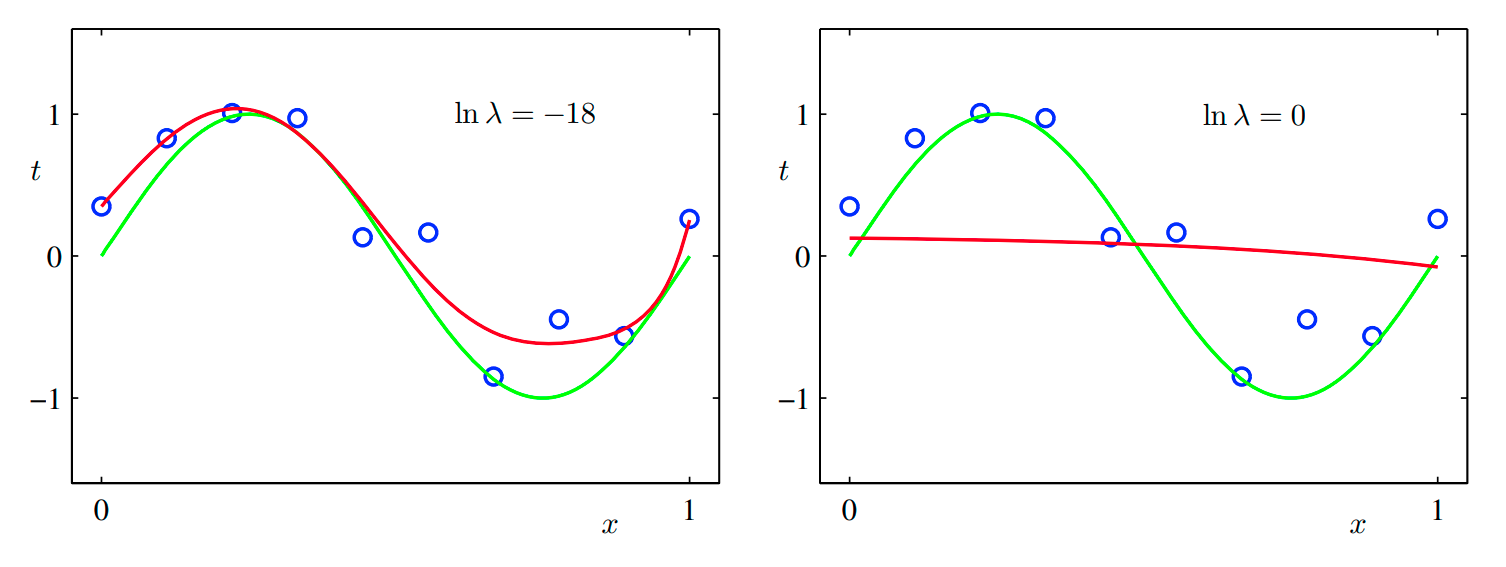
위의 그림을 보면 M= 9인 경우 λ\lambda의 값을 변경시켜가며 피팅한 결과를 알 수 있다.
lnλ=−18ln\lambda = -18의 경우 과적합이 많이 줄어들어 좋은 피팅 결과를 보이고 있고, lnλ=0ln\lambda = 0의 경우 피팅 결과가 좋지 않은 것을 알 수 있다. 아래 표를 보면 너무 큰 λ\lambda 값이 너무 클 경우 다항식의 계수의 크기가 많이 줄어든 것을 확인할 수 있다.

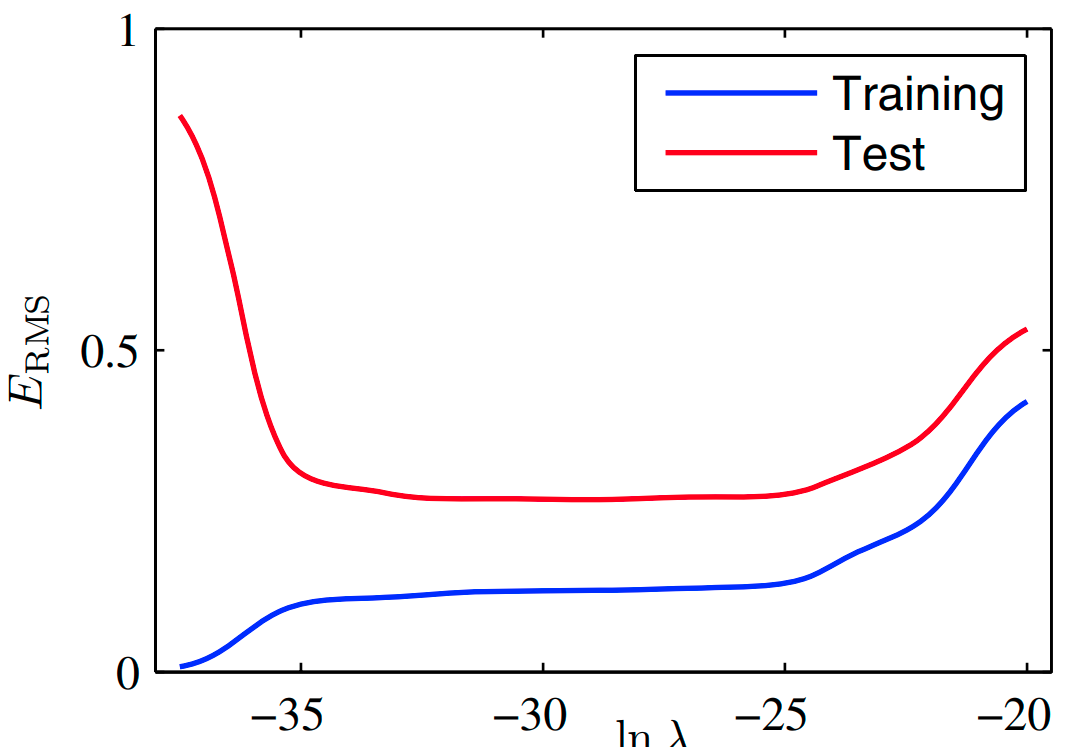
아래의 그림을 보면 정규화를 통해 trainset에 대한 error와 testset에 대한 error가 비슷한 양상을 띄게한 것을 확인할 수 있다.

lasso(L1 regularization)
E(w)=12∑n=1N{y(xn,w)−tn}2+λ∑j=1M∣wj∣E(\boldsymbol{w})=\frac{1}{2}\sum_{n=1}^{N}\{y(x_{n}, \boldsymbol{w})-t_{n}\}^{2}+\lambda \sum_{j=1}^{M}|w_{j}|

ridge(L2 regularization)
E(w)=12∑n=1N{y(xn,w)−tn}2+λ∑j=1Mwj2E(\boldsymbol{w})=\frac{1}{2}\sum_{n=1}^{N}\{y(x_{n}, \boldsymbol{w})-t_{n}\}^{2}+\lambda \sum_{j=1}^{M}w_{j}^{2}

검증?

지금까지의 결과를 바탕으로 모델을 잘 선택하는 단순한 방법을 생각해볼 수 있는데, 이는 데이터셋을 trainset과 validationset으로 나누는 것이다.
trainset은 계수 w를 결정하는 데에 활용하고, validationset은 모델의 복잡도를 최적화하는 데에 활용하는 방식이다.
대부분의 경우 이렇게 dataset을 나누면 데이터를 낭비하게 되므로 더 좋은 방식을 고려해야 한다.

profile
임용택
다음 포스트

[PRML정리]1.2 확률론

0개의 댓글

관련 채용 정보