[PRML정리]1.2 확률론

패턴 인식 분야에서 중요한 개념 중 하나는 바로 "불확실성". 1.5절에서 논의할 의사 결정 이론과 함께 활용하면 부족한 정보가 주어져도, 완전하지 않은 제약 조건 하에서도 최적의 예측을 시행할 수 있게 된다.

---

기본적인 컨셉 잡고 갑니다.

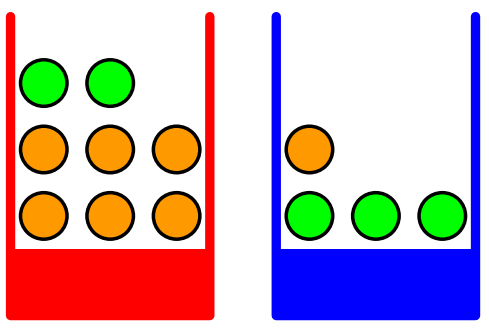
• 빨간 상자에는 사과 두 개, 오렌지 여섯 개가 있다.
• 파란 상자에는 사과 세 개, 오랜지 한 개가 있다.
• 랜덤하게 상자 하나를 골라 임의로 과일을 꺼내고, 과일을 확인 후 도로 상자에 집어 넣는다.
• 빨간 상자를 고를 확률은 40%, 파란 상자를 고를 확률은 60%이고, 상자 안에서 과일을 고를 확률은 동일하다.
• 예시에서 상자와 과일의 정체는 확률 변수이다.
• 상자는 B로 칭할 것이고 이는 r(red), b(blue) 중 하나의 값을, 과일은 F로 칭하는데 이는 o(orange), a(apple) 중 하나의 값을 취한다.
• 어떤 사건의 확률을 $\frac{특정 사건이 일어나는 횟수}{무한번 시도한 사건의 횟수}$ 라 정의해보자.
  그렇다면, 각 확률은 [0, 1]구간에 존재할 것이고 가능한 사건들의 모든 결과값을 포함한 경우 확률의 합이 1이 될 것이다.

---

합의 법칙, 곱의 법칙?

선택 과정에서 사과를 고를 확률?
오렌지를 선택했을 대 우리가 선택한 상자가 파란색일 확률?

이런 질문들에 답하기 위해 필요한 개념, "합의 법칙", "곱의 법칙"

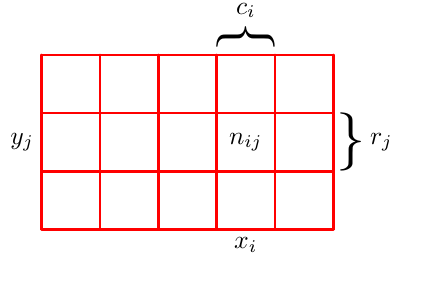
위의 그림에서 생각해보자.
여기엔 두 가지 확률변수 X, Y가 있다. X는 $x_{i}(i=1,2,...,M)$ 중 아무 값을, Y는 $y_{j}(j=1,2,...,L)$중 아무 값을 취할 수 있다.
$Y$값에 상관 없이 $X=x_{i}$인 사건의 개수를 $c_{i}$, $X$값에 상관 없이 $Y=y_{j}$인 사건의 개수를 $r_{j}$, $X=x_{i}, Y=y_{j}$인 사건의 개수를 $n_{ij}$라 하겠다.

결합 확률
$X=x_{i}, Y=y_{j}$인 확률을 $p(X=x_{i}, Y=y_{j})$로 적고 이를 $X=x_{i}, Y=y_{j}$일 결합 확률(joint probability)이라 한다. 식으로는 $p(X=x_{i}, Y=y_{j})=\frac{n_{ij}}{N}$으로 쓴다.

합의 법칙, 주변 확률
$p(X=x_{i})=\frac{c_{i}}{N}$에서 $c_{i}=\sum_{j}n_{ij}$이다.
따라서, $P(X=x_{i})=\sum_{j=1}^{L}p(X=x_{i},Y=y_{j})$이다.

이를 확률의 합의 법칙이라 하고, 여기서 $p(X=x_{i})$를 marginal probability라 한다.

곱의 법칙, 조건부 확률
$X=x_{i}$만 고려했을 때 그것 중 $Y=y_{j}$인 사건의 비율을 생각해볼 수 있고, 이는 수식으로 $p(Y=y_{j}|X=x_{i})$와 같이 쓸 수 있다. 이를 조건부 확률이라고 한다.
$p(Y=y_{j}|X=x_{i})=\frac{n_{ij}}{c_{i}}$이고, 이를 통해 다음의 식을 도출해낼 수 있다.
$p(X=x_{i}, Y=y_{j})=\frac{n_{ij}}{N}=\frac{n_{ij}}{c_{i}} \frac{c_{i}}{N}=p(Y=y_{j}|X=x_{i})p(X=x_{i})$
이를 확률의 곱의 법칙이라 한다.

---

베이즈 정리(Bayes' theorem)

위에서 정리한 곱의 법칙과, 확률의 대칭성 $p(X, Y)=p(Y,X)$를 이용해 다음의 식을 도출해낼 수 있다.
$p(Y|X)=\frac{p(X,Y)}{P(X)} = \frac{p(X,Y)}{P(Y)} \frac{P(Y)}{P(X)}= \frac{P(X|Y)P(Y)}{P(X)}$
위의 식을 베이즈 정리(Bayes' theorem)라 한다.

앞서 상자/오렌지/사과 예시를 다시 생각해보자.

빨간색 상자를 선택할 확률은 40%, 파란색 상자를 선택할 확률은 60%이므로 아래와 같이 쓸 수 있다.
$p(B=r) = 4/10$
$p(B=b) = 6/10$

상자가 주어졌을 때, 사과, 오렌지를 선택할 확률은 아래의 네 가지로 쓸 수 있다.
$p(F=a|B=r) = 1/4$ - 식a
$p(F=o|B=r) = 3/4$ - 식b
$p(F=a|B=b) = 3/4$ - 식c
$p(F=o|B=b) = 1/4$ - 식d

합의 법칙과 곱의 법칙을 이용해 사과를 고를 전체 확률을 구하면 아래와 같다.
$p(F=a) = p(F=a|B=r)p(B=r) +p(F=a|B=b)p(B=b)=\frac{1}{4}\frac{4}{10}+\frac{3}{4}\frac{6}{10}=\frac{11}{20}$

반대로, 어떤 과일을 선택했을 때, 그 과일이 오렌지고 이 오렌지가 어떤 상자에서 나왔는지 알고 싶다 해보자.
위의 식a-d는 상자가 주어졌을 때 과일에 대한 조건부 확률만을 알려준다.하지만, 베이지안 정리를 이용하여 조건부 확률을 뒤집으면 아래와 같은 식을 통해 문제를 해결할 수 있다.
$p(B=r|F=o)=\frac{p(F=o|B=r)p(B=r)}{p(F=o)}=\frac{3}{4}\frac{4}{10}\frac{20}{9}=\frac{2}{3}$

위의 과정에서

어떤 과일이 선택되었는지를 알기 전에 어떤 박스를 선택하였는지의 확률은 $p(B)$이고 이를 사전 확률 이라 한다.

선택된 과일이 오렌지라는 것을 알게 된다면 사건 F를 관측한 후의 확률이므로 사후 확률이라 한다.

독립 사건
$p(X, Y)=p(X)p(Y)$인 경우를 두 확률 변수가 독립적(independent)이라고 한다. 이 경우 곱의 법칙에 따라 $p(Y|X)=p(Y)$임을 알 수 있다.
이를 과일/상자 문제로 생각해보면 각각의 상자가 같은 수의 사과와 오렌지를 가지고 있다면 $p(F|B)=p(F)$가 되고, 사과/오렌지를 골랐는지는 어떤 상자를 골랐는지와는 무관한 문제가 된다.