[PRML정리]1.2.1 확률 밀도

지금까진 이산 확률에 대해 알아보았다.
이번 장에선 연속적인 변수에서의 확률에 대해 알아보겠다.

---

확률 밀도 함수, PDF(Probability Density Function)

임의의 실수 변수 $x$가 $(x, x+\delta x)$ 구간 안의 값을 가지고, $\delta \rightarrow 0$일 때 그 변수의 확률이 $p(x)\delta x$로 주어진다면, $p(x)$를 변수 $x$의 확률 밀도함수, PDF(Probability Density Function)라 한다.

$x$가 구간 $(a,b)$ 사이의 값을 가질 확률은

$p(x \in (a,b))=\int_{a}^{b}p(x)dx$

로 쓸 수 있다.

확률은 양의 값을 가지고, $x$의 값은 실수축 상에 존재해야 한다.
따라서, 확률 밀도 함수 $p(x)$는 아래의 두 조건을 만족시킨다.
$p(x) \geq 0$
$\int_{-\infty}^{\infty}p(x)dx = 1$

---

확률 변수의 transformation?

추가 예정

---

누적 분포 함수, CDF(Cumulative Distribution Function)

$x$가 $(-\infty,z)$에 속할 퐉률은 누적 분포 함수로 아래와 같이 표현된다.
$P(z)=\int_{-\infty}^{z}p(x)dx$

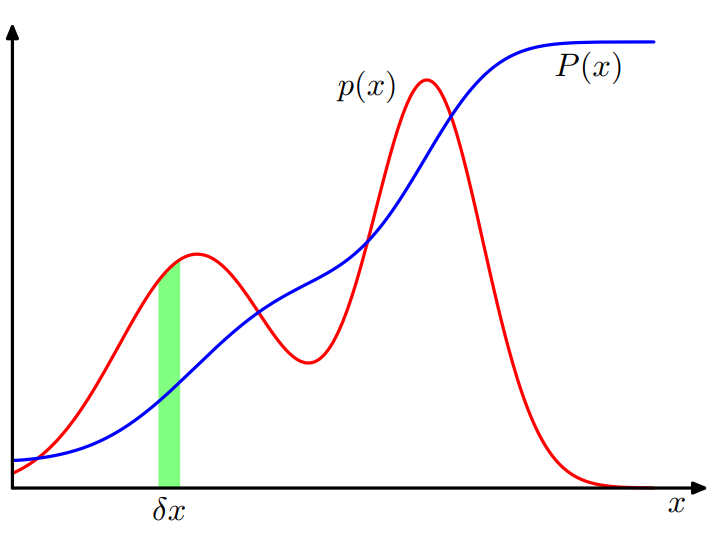
반대로, $P'(x)=p(x)$이다.

여러 개의 연속적인 변수 $x_{1}, x_{2}, ..., x_{D}$가 주어지고 이 변수들이 벡터 $\boldsymbol{x}$로 표현된다면 결합 확률 밀도 함수 (joint probability density function) $p(\boldsymbol{x})=p(x_{1},x_{2},...,x_{D})$를 정의할 수 있다.
다변량 확률 밀도는 아래의 식을 만족한다.

$p(\boldsymbol{x}) \geq 0$
$\int_{-\infty}^{\infty}p(\boldsymbol{x})d\boldsymbol{x} = 1$

---

확률 질량 함수

$x$가 이산 변수일 경우 $p(x)$를 확률 질량 함수라고 부른다.