ch11. Comparison to Other Types of Generative Models

VAE variational lower bound를 구하여 학습하는 방식

---

1. Autoregressive models

• 단점
  : 계산적인 측면에서 시퀀시라서, 여러 데이터들을 샘플링시에 한계가 있음.

• 장점
  : 시계열(time - series)에서 사용됨, 이전 데이터로 현재 데이터 예측함.
  : p(x) likelihood를 분명하게 계산가능함
  : 학습도 단순함

FVBN (fully visible belief network)

• 데이터의 가능성을 명확하게 구할 수 있는 장점
• 이전 픽셀로 현재 픽셀의 product of 1d distribution의 chain rule로 likelihood를 표현하게 됨. 이전의 픽셀들의 값이 픽셀 값에 대한 복잡한 분포이므로 이를 Neural network로 표현하게 됨.

1. PixelRNN - 다루기 쉬운 density function사용

• RNN에서의 Autoregressive(이전데이터로 현재 데이터를 예측하고자함)
• 처음에는 랜덤으로 정해지고, 점차적으로, 오른쪽과 아래의 값을 예측하고, 예측된 값을 기반으로 추가적으로 오른쪽과 아래의 값을 지속적으로 하여 픽셀들의 값을 예측하는 것이 PixelRNN임
  

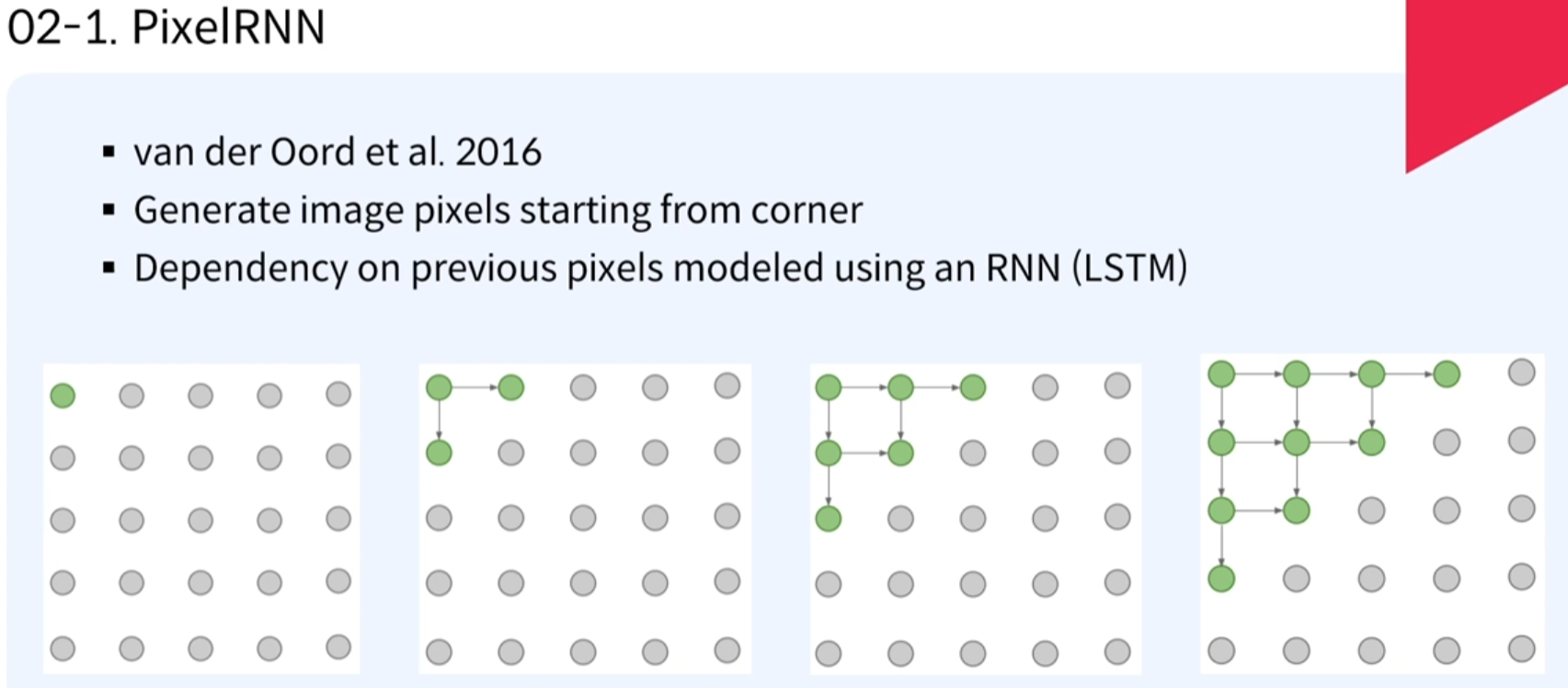
2. PixelCNN - 다루기 쉬운 density function사용

• 시작은 좌상단에서부터 우하단까지 생성하게 됨.
• cnn의 장점은 학습이 빠르게 진행됨 -> rnn보다 연산이 parallelize됨
• 그래도 32x32이미지의 생성 경우에도 network가 1024번을 통과해야함

---

2. VAE(variational autoencoders)

• 목표
  : 정규화된 latent vertor인 z의 값으로 조건을 만족하는 이미지 x를 맞추는 것임

• 장점
  : 다루기 어려운 density function사용
  : 모든 픽셀을 한번에 예측하게 된다는 점
  : 해석가능한 잠재벡터
  : 규칙으로 접근한 생성모델
  : 추론을 허락하지만, 다른 task에서 특징 표현들에 유용함

• 단점
  : 근산화된 값을 이용하므로, 오차가 발생할 수 있음.
  : 성능이 좋지 않음, blurring 혹은 lower한 qulity임.

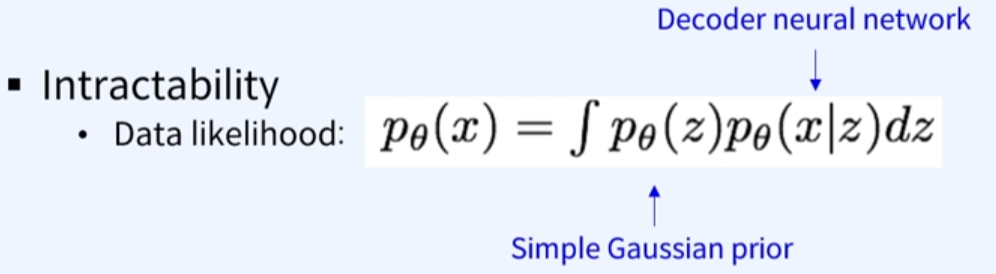
• 보통 p(z)는 심플한 가우시안 분포 등이 있음.
• p(x|z)의 경우는 complex한 분포(이미지 생성으로)로 이를 Neural network로 표현함.

• 그림처럼 거의 무한대에 가까운 다루기 어려운 분포들임.
• 이를 위해, 몬테카를로 추정을 통하지만, 이는 높은 분산이 생기게 됨.

1. 해결책

• 사후 density인 $p_{\theta}$(x|z)를 근접하게 하는 인코더 네트워크인 $q_{\phi}(z|x)$로 학습하는 것을 의미한다.

• KL-divergence (항상 0보다 크다), 2개의 확률분포 a, b중에 어느 한 분포에 얼만큼 다른지를 수치로 봄.

• 인풋이미지 x라고 했을때, 사후 density를 근접하게 하는 인코더 네트워크인 $q_{\phi}(z|x)$로 학습시키면, 다음과 같이 평균분포과 시그마분포를 구함

• 다음에서 우리는 KL-divergence로 평균분포와 시그마분포를 (0~1)로 정규화 후에 다른지를 계산함.

• 이제 z를 샘플링하게 되는데, 일반적인 샘플링은 계산그래프를 생성할 수 없으므로, 이는 기울기 신호들이 인코더 네트워크까지 도달하지 않는다. 이를 위해 우리는 샘플링을 계산 그래프를 구할 수 있도록 한다.
  

• 이제 우리는 z를 decoder에 넣어주고,
  

• 

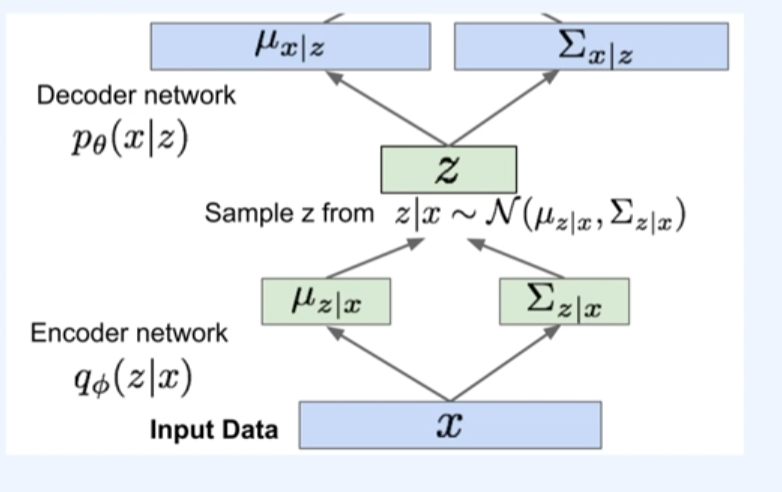
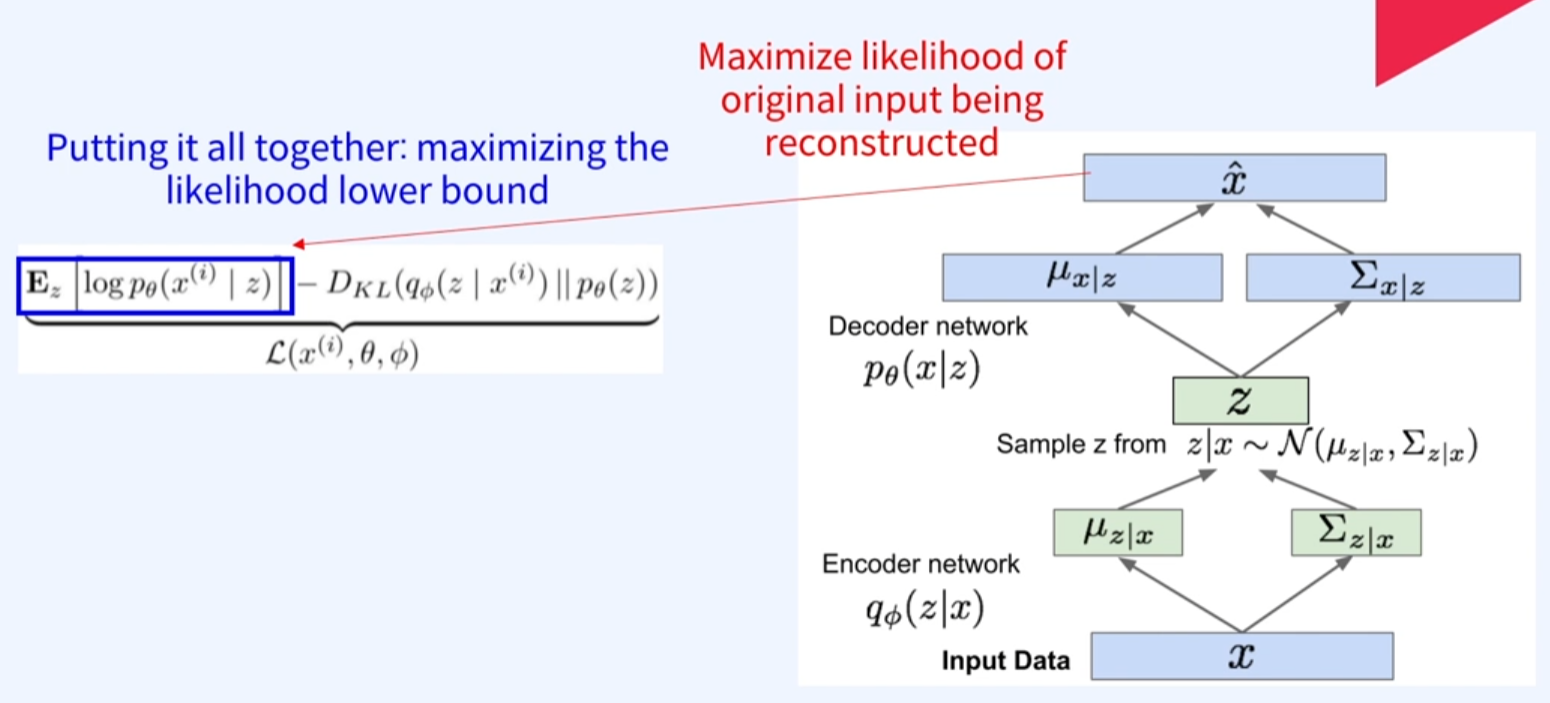
• 이렇게 구해진 $\bar{x}$를 통해서 최대화하는 likelihood를 reconloss를 통해서 구함.
  

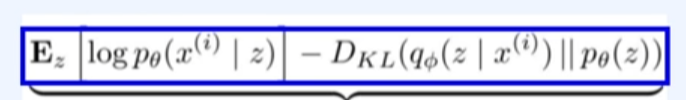
• 위의 과정을 minibatch만큼 계속해서 학습하는 것임.