11. Container With Most Water

문제링크: https://leetcode.com/problems/container-with-most-water/

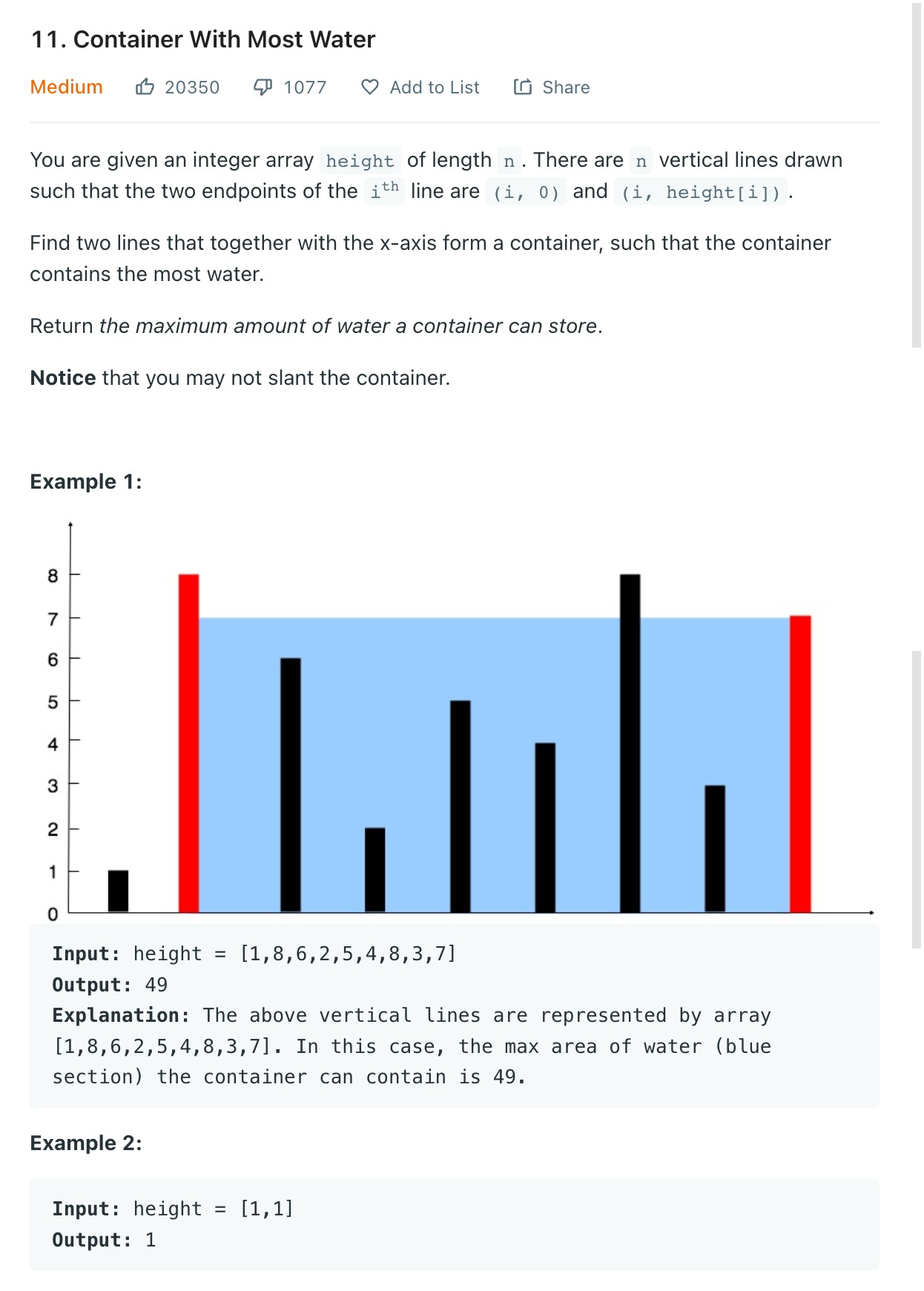
수직 선 두개를 골라 사이를 물로 채웠을 때 넘치지 않는 물의 최대 너비를 구하는 문제다.

Solution

1. Brute force

우선 가장 직관적이고 정확한 완전 탐색을 해보기로 했다. 너비를 구하는 함수만 만들면 할 수 있기 때문에 바로 구현해 보았다.

Algorithm

• 물의 너비를 구하는 함수 가로 * 둘 중 작은 높이를 만든다.
• 이중 반복문을 돌며 물의 너비를 구하고 결과와 비교해 갱신한다.

var maxArea = function(height) {
  // Brute force
  const getWaterVolume = (idx1, idx2) => {
    return Math.abs(idx1 - idx2) * Math.min(height[idx1], height[idx2]);
  }
  let result = 0;
  for (let i = 0; i < height.length; i++) {
    for (let j = i + 1; j < height.length; j++) {
      result = Math.max(result, getWaterVolume(i, j));
    }
  }
  return result;
};

결과는 시간 초과가 나왔다. 가장 단순한 O(n^2)의 알고리즘으로는 테스트 요건을 만족할 수 없었다. 계산을 하는데 두 지점만 사용한다는 점, 높이가 높아지지 않는다면 범위를 줄여도 더 좋은 결과가 나오지 않는 등 문제의 성질을 이용해 다른 방법을 찾아보기로 했다.

2. 2 pointers

특정 범위 (i ~ j)에서 어떤 결과가 나올 때, (i-1 ~ j) 또는 (i ~ j+1)의 범위를 결과에서 pruning 할 수 있을 때 sliding window 나 2 pointers를 이용해 시간 복잡도를 크게 단축시킬 수 있다.

이번 문제는 너비의 요인으로 가로와 세로가 있다. 이때 좌표의 변환으로 가로가 줄어든다면 세로가 늘어나야 탐색할 만한 가치가 있다. 즉, 가로와 세로가 모두 줄어들거나 그대로라면 pruning을 할 수 있다.
가로의 요소는 둘의 index로 정해지고 세로 는 둘 중 작은 기둥에 의해 정해진다. 위의 조건대로 가로를 줄이기 위해서 좌, 우 기둥 중 하나를 가까운 쪽으로 옮긴다고 할 때, 큰 기둥을 옮기게 되면 세로는 변하지 않거나 줄어들게 된다. 즉 너비의 향상이 이뤄질 수 없기 때문에 탐색할 필요가 없다. 따라서 작은 기둥을 옮기다면 최소 세로의 향상을 기대해 볼 수 있기 때문에 두 개의 높이를 비교해 가면서 하나의 가지수를 pruning할 수 있다. 만약 두개의 높이가 동일하다면 둘 중 하나만 옮겨서는 세로의 길이가 변하지 않거나 줄어들기 때문에 둘 다 옮겨서 나머지 경우의 수를 탐색한다.

Algorithm

• 양 쪽 끝에서 left와 right를 지정한다.
• 둘의 높이를 비교해 result와 비교해 갱신하고 다음과 같이 단방향으로 진행한다.
  1. 길이가 같을 때, 둘 다 가깝게 한다.(하나만 줄이면 세로의 향상을 기대할 수 없음)
  2. 길이가 다르면 높이가 작은 기둥을 가깝게 한다.(큰 기둥은 줄여도 작은 기둥에 의해 세로의 향상을 기대할 수 없음)

var maxArea = function(height) {
  // 2 pointer
  // 양쪽 끝에서 시작, 더 작은거를 접근시키면서 계산 (이유 큰 막대는 옮겨봤자 가로길이만 줄어들기 때문)
  // 길이가 같을 경우 둘다 줄임 (하나만 줄여도 가로길이만 줄어들기 때문)
  const getVolume = (left, right) => {
    return (right - left) * Math.min(height[left], height[right]);
  }
  
  let left = 0, right = height.length - 1;
  let result = 0;
  while (left < right) {
    const cal = height[left] - height[right];
    if (cal === 0) {
      result = Math.max(result, (right - left) * height[left]);
      left++;
      right--;
    } else if (cal < 0) {
      result = Math.max(result, (right - left) * height[left]);
      left++;
      
    } else {
      result = Math.max(result, (right - left) * height[right]);
      right--;
    }
  }
  return result;
 };

탐색을 하기 위한 매 분기에서 2종류의 경우의 수를 하나로 pruning할 수 있다는 점이 2 pointers의 장점이다. 시간 복잡도는 O(n)으로 기존의 O(n^2)에 비해 상당히 향상되었다.