1937. Maximum Number of Points with Cost
문제링크: https://leetcode.com/problems/maximum-number-of-points-with-cost/description/

배열이 주어지고 한 행에 하나의 원소를 고를 수 있다. 각 원소를 원소들의 합으로 점수를 얻게 되는데, 연속된 행에서 고른 원소의 열 좌표가 다를 경우 좌표차이만큼 점수를 뺀다.
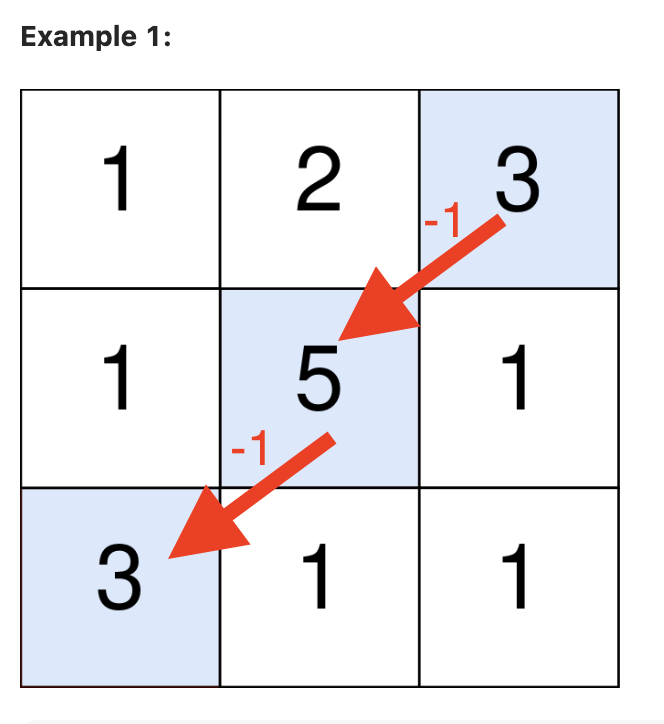
Ex1 총 점수: 3 + (-1) + 5 + (-1) + 3 = 9
얻을 수 있는 점수 중 최대 점수를 구해야 한다.
Solution
1. Dynamic programming
points[i][j]에 도달할 때 최대 점수를 얻으려면 points[i-1]의 각 열에 도달할 때 최대 점수를 알고 있으면 points[i-1][k] 와 points[i][j]의 abs(k - j)를 이용해 도달할 수 있는 최대 점수를 얻을 수 있다.
0 ~ j의 모든 k에 대해
각 단계에는 이전 단계의(DP[i - 1]) 정보만 필요하기 때문에 이를 memPrev의 O(n) 공간만 사용한다. 초기값은 points[0]가 된다.
Algorithm
- 점수의 시작점에는 패널티가 없으므로
memPrev를points[0]로 저장한다. DP[i][j]를 연산하기 위해 이중 루프를 생성한다.- 위의 수식에 따라
maxFromPrev를 얻고 자기 자신의points[i][j]를 더해DP[i][j]를 구한다. - 모든 연산이 끝난 후 마지막에 남은
memPrev의 최대값을 결과로 반환한다.
var maxPoints = function(points) {
const rLen = points.length;
const cLen = points[0].length;
let memPrev = points[0]; // DP 초기값
// DP[i] 연산
for (let i = 1; i < rLen; i++) {
const memCur = [];
// DP[i][j] 연산
for (let j = 0; j < cLen; j++) {
// 도달할 때 최대 점수 연산
let maxFromPrev = -Infinity;
memPrev.forEach((el, idx) => {
maxFromPrev = Math.max(maxFromPrev, el - Math.abs(idx - j));
})
memCur[j] = maxFromPrev + points[i][j];
}
memPrev = memCur; // DP 결과 갱신
}
return Math.max(...memPrev);
};테스트 케이스를 모두 완료하지 못하고 TLE 되었다. 공간 복잡도는 O(n)으로 최대한 줄였지만 시간 복잡도에서 O(mn^2)인 것이 문제가 되었다. DP를 위해 이중루프를 도는 것은 어쩔 수 없지만 최대값을 구하는 연산을 매번 O(n)의 반복을 통해 얻는 부분을 개선하면 시간 복잡도를 줄일 수 있을 것으로 보인다.
2. DP with O(mn)
위에서 구한 DP 점화식을 그대로 이용하면서 문제의 특성을 이용해 효율적으로 동작하도록 개선해보려 했다. 만약 열간 거리로 인한 점수 패널티 부분이 없다면 O(mn)의 알고리즘으로 쉽게 구현할 수 있다. 그렇다면 거리로 인해 생기는 패널티 부분은 매번 DP[i-1]의 O(n)시간을 들여 탐색해야만 구할 수 있을까? 단순한 -1 -2 -3 ... 의 계산인데 말이다. 이 부분도 DP의 관점으로 접근할 수 있었다.
계산의 분기가 되는 abs를 기준으로 DP[i][j]의 범위를 나눠보면 DP[i-1][k]에서 k <= j 인 경우, k > j인 경우로 볼 수 있다. 이 두가지 경우로 문제를 나눠서 [i]보다 왼쪽의 열에서 계산하는 경우와 오른쪽에서 계산하는 경우로 나누었다.
왼쪽에서의 예시를 보면 DP[i-1]이 [4, 2, 3]이라고 하자.
DP[i][0]에 왼쪽에서 도달하는 방법은 4자신밖에 없다.DP[i][1]에 왼쪽에서 도달하는 방법은 4-1과 2 두가지로 큰 값은 3이다.DP[i][2]에 왼쪽에서 도달하는 방법은 4-2, 2-1, 그리고 3인데 이때 4-2와 2-1은 이미DP[i][1]을 통해 비교했었던 값들에 -1에 불과하므로DP[i][1] - 1을 그대로 사용해도 된다.
즉 왼쪽에서 접근하는 경우는 DP[i-1]를 한번만 돌아도 O(n)의 시간을 통해 DP[i]를 모두 구할 수 있다.
반대로 오른쪽에서 접근하는 경우도 동일하며 왼쪽에서 접근한 값과 오른쪽에서 접근한 값 중 최대로 DP[i][j]를 얻을 수 있다.
Algorithm
memPrev에points[0]의 초기값을 저장한다.leftDP를 구하기 위해 0부터 순회한다.leftMax가leftDP[i][j]의 역할을 하며 위의 수식을 연산한다.memCur에leftDP값들을 우선저장한다.rightMax가rightDP[i][j]의 역할을 한다.rightMax와memCur[j]에 저장되어있는leftMax를 비교해 마지막 수식을 연산한다.memPrev를 갱신한다.- 마지막으로 남은
memPrev중 최대값을 반환한다.
var maxPoints = function(points) {
const rLen = points.length;
const cLen = points[0].length;
let memPrev = points[0]; // 초기값
for (let i = 1; i < rLen; i++) {
const memCur = new Array(cLen);
// 왼쪽 -> 오른쪽
let leftMax = -Infinity;
for (let j = 0; j < cLen; j++) {
leftMax = Math.max(leftMax - 1, memPrev[j]);
memCur[j] = leftMax;
}
// 왼쪽 <- 오른쪽
let rightMax = -Infinity;
for (let j = cLen - 1; j >=0; j--) {
rightMax = Math.max(rightMax - 1, memPrev[j]);
// left는 이미 저장된 값, rightMax와 비교해 큰 값이 최종 DP값
memCur[j] = Math.max(memCur[j], rightMax) + points[i][j];
}
memPrev = memCur;
}
return Math.max(...memPrev);
};
총 시간 복잡도 O(mn), 공간복잡도 O(n)을 만족한다. DP로 문제에 접근할 때는 주어진 문제의 특징을 최대한 활용해야 한다고 느꼈다.

