95. Unique Binary Search Trees II
문제링크: https://leetcode.com/problems/unique-binary-search-trees-ii/description/
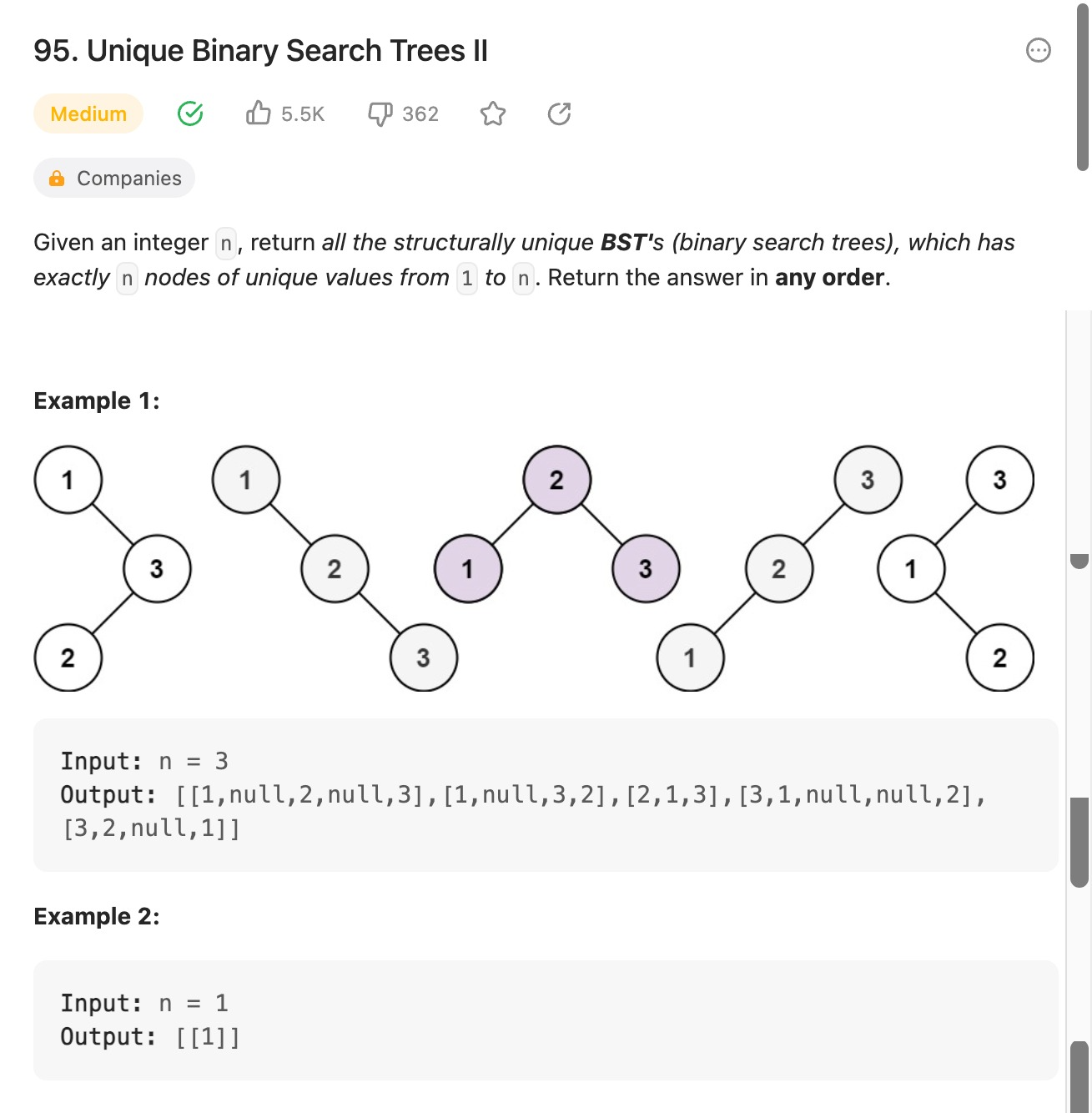
노드가 1~n까지 있는 이진트리의 가능한 모든 형태를 구하는 문제다.
Solution
Divide and conquer
기존에 n개 노드의 이진트리의 개수를 구하는 문제를 풀었었다. 이진트리의 형태는 루트 노드를 만든 후 왼쪽과 오른쪽에 가능한 노드의 종류를 모두 구하고 이를 다시 작은 문제로 나누는
의 형태로 주어진 문제를 해결할 수 있었다. 이번에도 같은 방식으로 접근해 루트를 기준으로 왼쪽 노드, 오른쪽 노드를 구하는 작은 문제로 나누어 접근했다. 기존엔 bottom-up으로 접근했다면 이번에는 아래에 설명된 offset값의 범위를 미리 정하기 힘들기 때문에 top-down으로 접근했다.
generateTrees(n)의 경우 1~n의 노드를 이용해 이진트리를 만든다. 이 때 작은 문제로 나누게 되면 루트를 k로 정했다면 1~k-1, k+1~n의 좌우 노드들이 필요하다. 1~k-1은 1~n과 형태가 같지만 k+1~n의 경우는 1에서 시작하지 않기 때문에 각각 1에서 k까지 옮긴 값을 offset이라고 하고 getTrees(nodeCount, offset)을 통해 결과를 얻었다.
Algorithm
getTrees의 결과를 저장하기 위해 dp배열을dpTrees로 정의했다. ([nodeCount][offset]으로 저장)generateTrees(n)은getTrees(n, 0)을 반환한다.getTrees에서nodeCount가0인 경우는null이 담긴 배열을 반환한다.dpTrees[nodeCount]가 없는 경우 이중배열을 추가해준다.dpTrees[nodeCount][offset]이 없는 경우 새로 생성한다.- 왼쪽노드의 개수가
0개 ~nodeCount - 1까지 가능하고 이를i로 반복한다. - 왼쪽 노드 개수를 정하면 왼쪽 노드 리스트는
getTrees(i, offset)을 통해 얻을 수 있다. - 오른쪽 노드 리스트도
getTrees(nodeCount - 1 - i, i + 1 + offset)으로 얻을 수 있다. - 왼쪽과 오른쪽에 가능한 트리종류를 모두 얻었으면 이중반복을 통해 각각 하나씩 연결해
treeResults에 추가한다. - 해당 값을
dpTrees[nodeCount][offset]에 저장하고 반환한다.
var generateTrees = function(n) {
// 모양만들기 루트노드 삽입하고 (왼쪽에 n개) (오른쪽에 전체 - n)개로 추가 가능
// 방법) 루트노드 (개수에 맞춰서 숫자 정함) make(n) nodes 함수는
// DP 개수, offSet offSet0: [1-2 , 2-1], offSet1: [2-3, 3-2]
const dpTrees = [];
const getTrees = (nodeCount, offset) => {
if (nodeCount === 0) return [null];
// dpTrees에 있으면 가져옴, 없으면 만들어서 가져옴
// dpTrees에 없으므로 생성해서 저장하고 가져옴
// dpTrees[nodeCount]가 아예 없을 때 배열 생성
if (!dpTrees[nodeCount]) dpTrees[nodeCount] = [];
// 좌우에 가능한 트리들을 가져와서 결과에 맞는 트리들을 만든다
if (!dpTrees[nodeCount][offset]) {
const treeResults = [];
for (let i = 0; i < nodeCount; i++) {
const leftTrees = getTrees(i, offset);
const rightTrees = getTrees(nodeCount - 1 - i, i + 1 + offset);
for (let leftTree of leftTrees) {
for (let rightTree of rightTrees) {
treeResults.push(new TreeNode(i + 1 + offset, leftTree, rightTree));
}
}
}
dpTrees[nodeCount][offset] = treeResults;
}
// 이제 존재하므로 가져옴
return dpTrees[nodeCount][offset];
}
return getTrees(n, 0);
};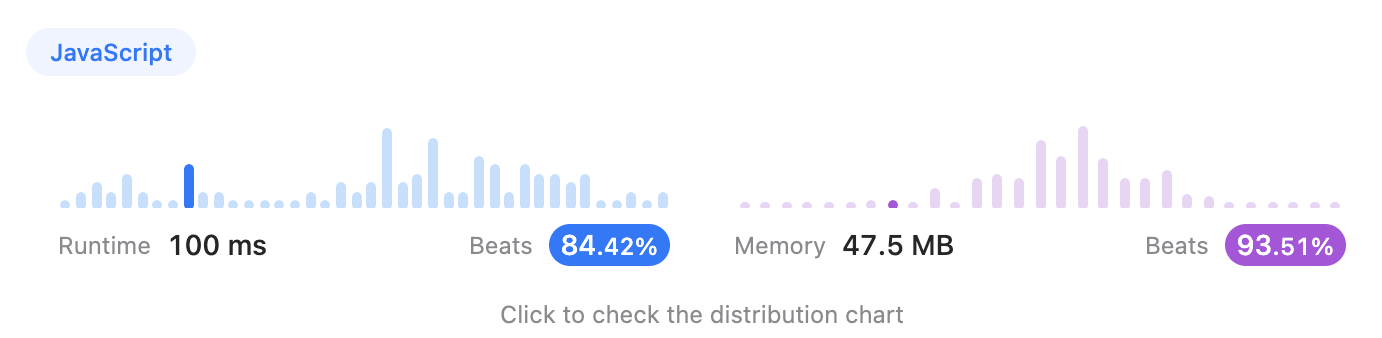
각 노드는 포인터로 연결되어 있기 때문에 모든 노드를 생성하는 것 보다 효율적이다. 마치 파스칼의 삼각형처럼 각 노드들이 구성되어 있고 dpTrees의 배열은 각각 노드를 포인터로 가지고 있어 복잡도는 노드의 개수를 따르고 catalan수열과 같다고 한다.

