42. Trapping Rain Water

문제링크: https://leetcode.com/problems/trapping-rain-water/

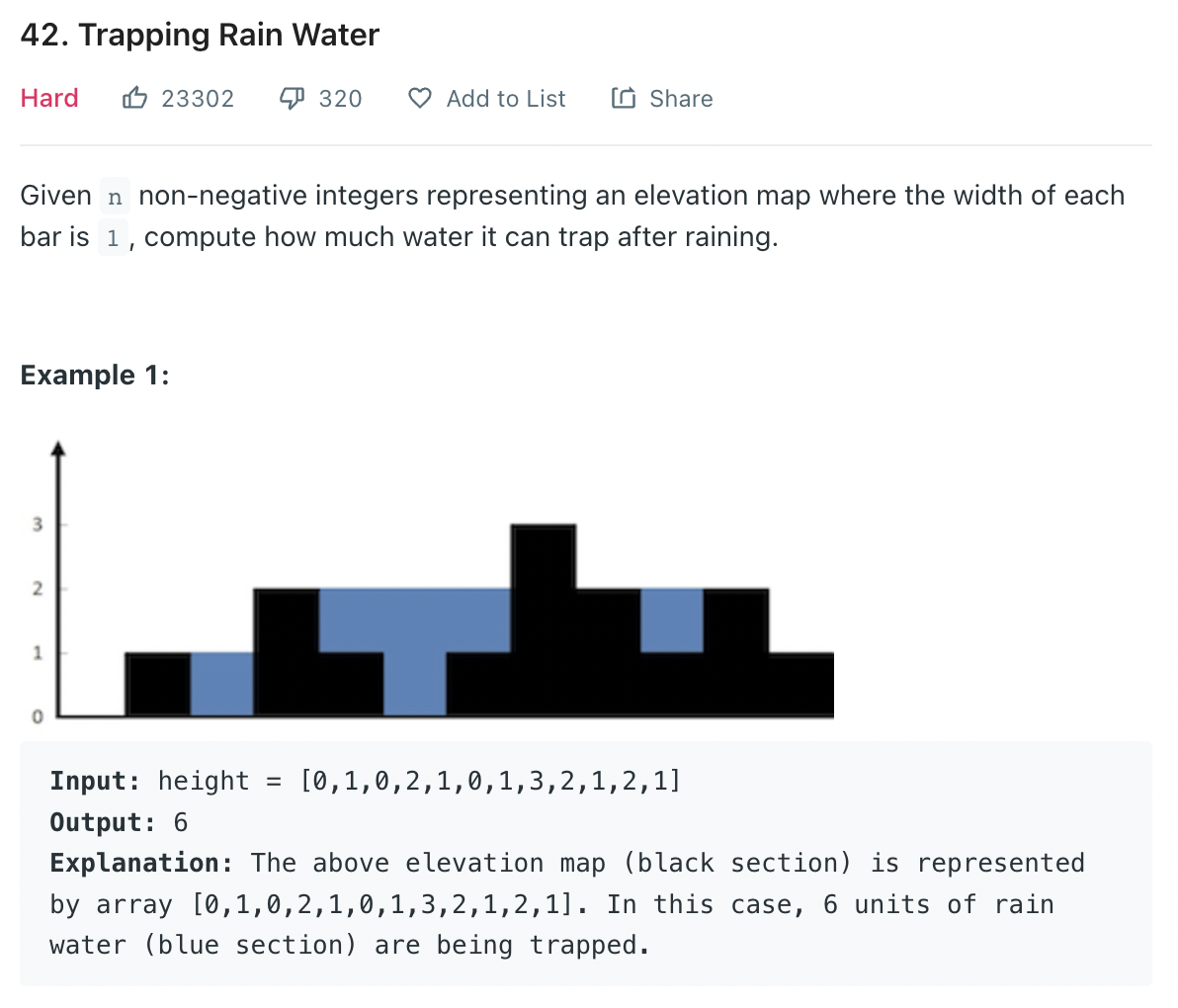
그림과 같은 막대그래프의 높이가 주어졌을 때, 비가 온다면 물이 고이는 양을 얻어야 한다.

Solution

2 pointers

이전에 물로 가둘 수 있는 최대 막대그래프 문제를 풀었었다. 링크:https://velog.io/@terrylim/LeetCode-11.-Container-With-Most-Water
해당 문제에서 완전탐색과 2 포인터를 이용한 문제풀이를 시도했었다. 이와 비슷한 방식으로 이번에도 2 포인터를 사용해 물이 갇히는 특성을 이용해보기로 했다.

메인 컨셉은 양쪽에 기둥이 있다면 큰 기둥은 높이에 영향을 끼치지 않는다는 것이다. 따라서 큰 기둥과 작은 기둥에 있어서는 작은 기둥만 움직여서 탐색한다면 물이 갇히는 경우의 수는 모두 탐색할 수 있다. 이 방법으로 기둥을 포함한 모든 물의 부피(total)를 계산하고 막대기둥의 부피(sumBlock)을 빼주면 결과를 얻을 수 있다.

Algorithm

• 2포인터를 위한 left, right, 현재까지 구한 높이(물은 한번 채우면 그 이하의 블록은 무시한다)prevHeight, 블록을 포함한 전체 부피total을 변수로 선언한다.

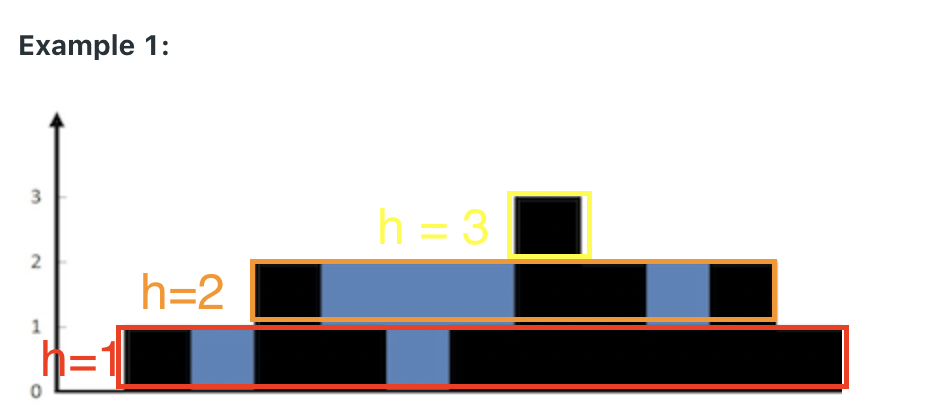
• 2포인터 반복문을 돌면서 curHeight은 현재 블록 중 낮은 높이가 되고 이 높이가 prevheight보다 높으면 새로운 물부피를 갱신한 것으로 total에 이 부피를 계산해준다. 이때 계산하는 방법은 다음과 같다.

  total += (right - left + 1) * (curHeight - prevHeight)
  

• 그림과 같이 새로 갱신한 높이curHeight와 기존과 높이prevHeight의 차이 만을 계산해 추가 부피를 구한다.

• 부피를 더한 후 높이가 낮은 부분의 포인터를 가깝게 옮기고 같을 경우는 둘다 옮긴다.

• 위 방식으로 전체 부피를 구한 후 height의 값을 모두 더해 블록(검은색)의 부피를 구한다.

• total - sumBlock을 통해 물의 부피만 남기고 반환한다.

var trap = function(height) {
  // 2 pointers
  let left = 0;
  let right = height.length - 1;
  let prevHeight = 0;
  let total = 0;
  while (left <= right) {
    const curHeight = Math.min(height[left], height[right]);
    if (prevHeight < curHeight) {
      total += (right - left + 1) * (curHeight - prevHeight);
      prevHeight = curHeight;
    }
    const compare = height[left] - height[right];
    if (compare <= 0) {
      left++;
    } 
    if (compare >= 0) {
      right--;
    }
  }
  const sumBlock = height.reduce((a, c) => a + c, 0);
  return total - sumBlock;
};

시간 복잡도 O(n) 공간 복잡도 O(1)로 효율적인 문제풀이를 했다. 너비를 구하는 부분도 높이차가 생긴 경우에만 하기 때문에 평평하고 긴 부피 ex)[1,0,0,0,0,0,0,0,0,...,1] 과 같은 경우에 계산하는 부분도 줄어들어 같은 O(n)알고리즘이더라도 매번 높이를 계산하는 알고리즘보다 경우에 따라서 더 효율적이다.