Arithmetic for Computers

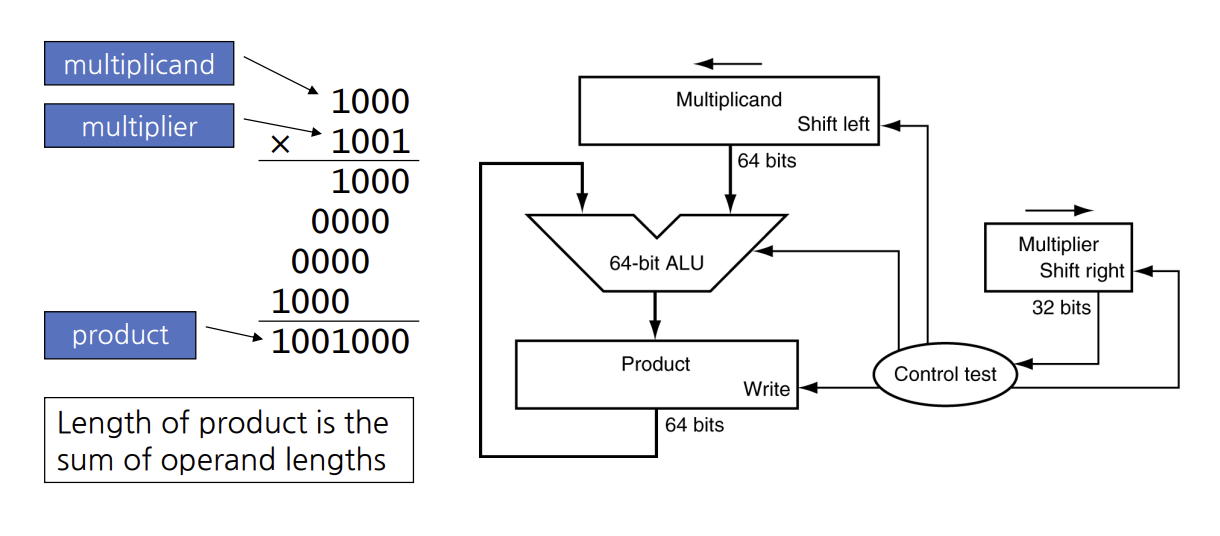
Floating Point

• scientific notation(과학적 표기법): 소수점 왼쪽이 한자리만 나타나게 하는 표기법

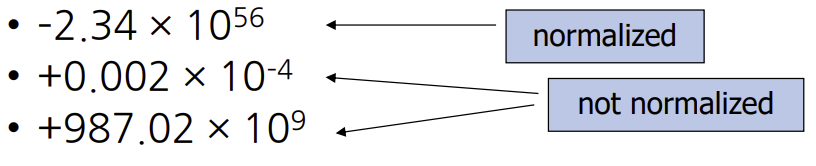
• normalized: scientific notation 중에서 일의 자리가 0이 아닌수

binary point

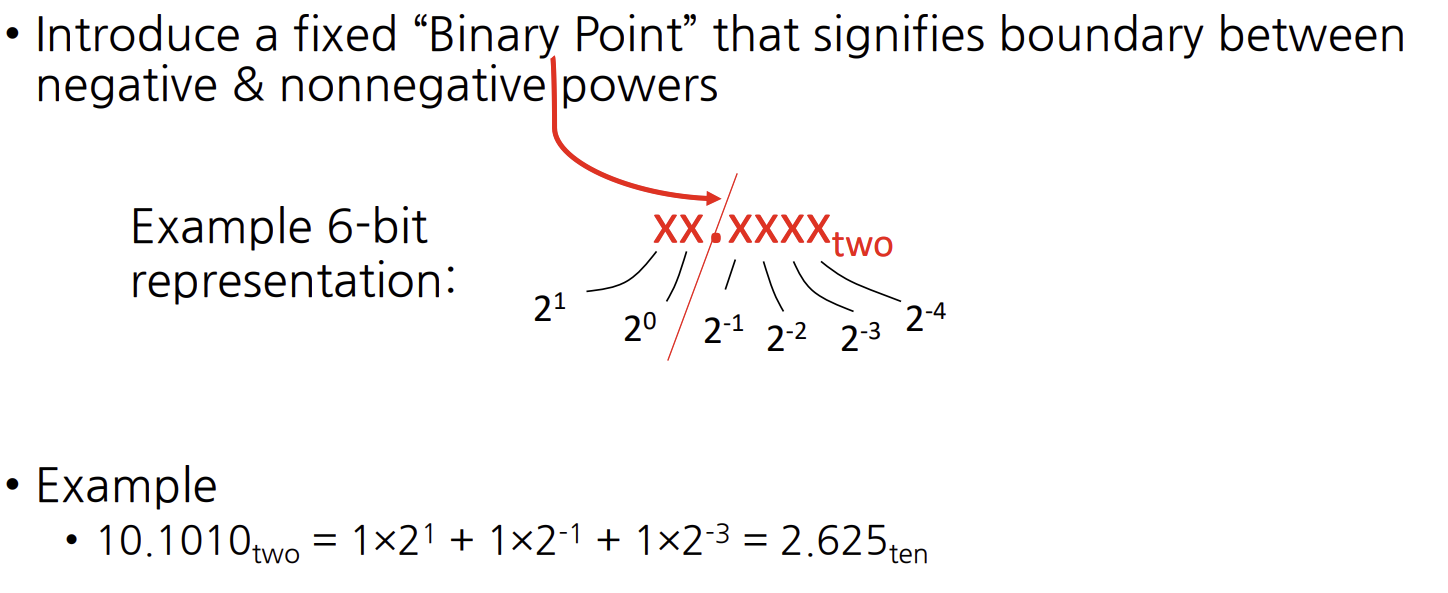
scientific Notation(Decimal)

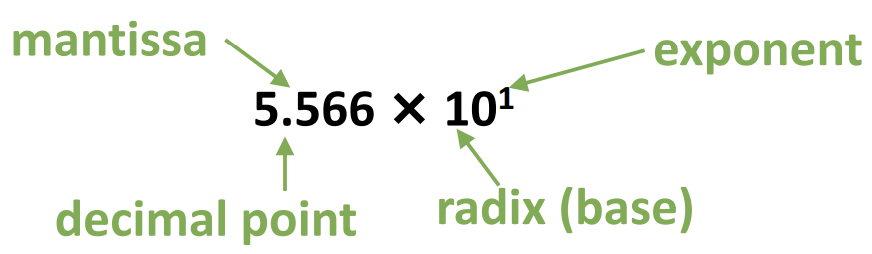
scientific Notation(Binary)

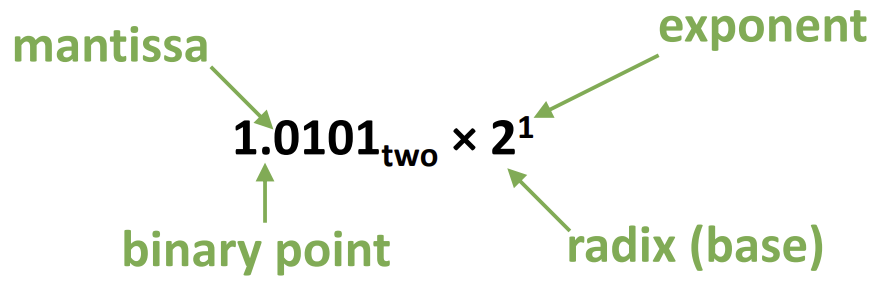
이러한 식으로 하는 컴퓨터 연산을 floating point 연산이라고 한다.

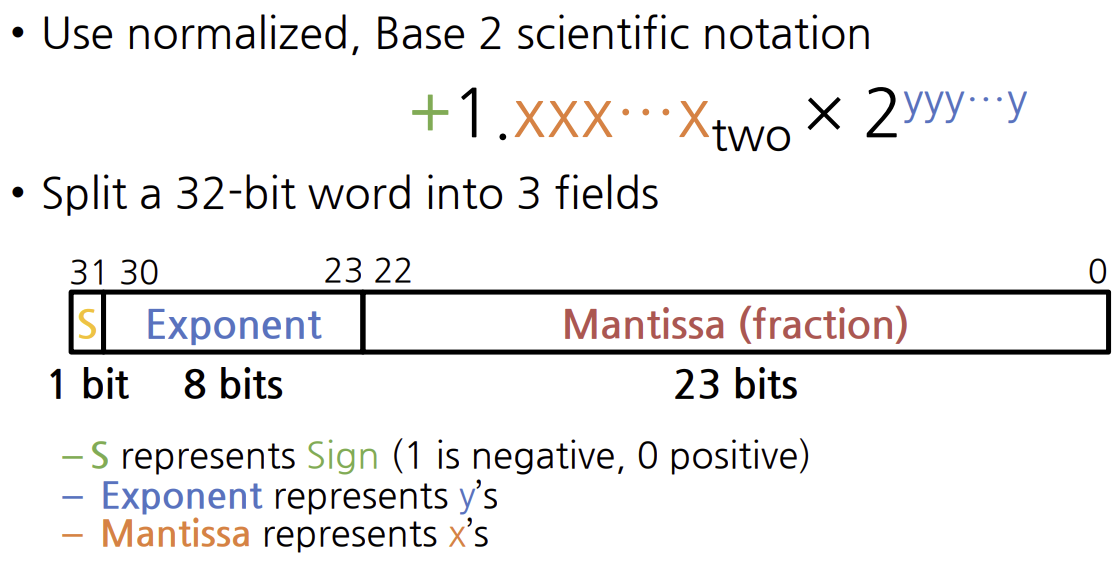
biased notation

• 가장음수인 지수를 00...0000(2)으로, 가장 양수인 지수를 11....111(2)로 표현하는 것이다.
• bias는 실제 값을 구하기 위해 부호없이 표현된 수에서 빼야 하는 상수를 말한다.
• 단일 정밀도 표현 방식에서는 bias 값 127을 사용한다.
  따라서 -1 은 -1+127 인 126 = 0111 1110(2)의 비트 패턴으로 표현된다. 그리고 +1은 1+127인 128로 표현된다.
• exponent 0은 01111 1111(2) = 127 이다.
• 2배 정밀도 표현방식에서 bias 값은 1023이다.
• 2배 정밀도 에서는 sign 1bit, Exponent 11 bits, Mantissa 20 + 32 bits이다.
• 정리하면 exp에는 127 더하면 되고, bias 127을 다시 빼주는 식을 만들어서 이진수로 나타내면 된다.

example

• -0.75를 이진 표현법에 따라 단일 정밀도 및 2배 정밀도를 표현해라
  $\frac{-3}{4}$ = $\frac{-11_2}{2^2}$ = $-0.11_2$ = $-1.1_2 \times2^{-1}$
  biased notation에 의해
  $-1.1_2\times2^{126- 127}$
  = $-1\times(1+ .1000, 0000, 0000, 0000, 0000, 0000)\times2^{126-127}$

비트는
1(sign) 011111111(exp)1000 0000 0000 0000 0000 0000(mantissa) 로 나타낼수 있다.

2배 정밀도는 bias 값만 1023으로 바꾸면 된다.
$-1\times(1+ .1000, 0000, 0000, 0000, 0000,..., 0000)\times2^{1022-1023}$
mantissa 자리에 20 + 32 bit만큼 채워져야 하기 때문에 뒷부분은 모두 0이다.

bias notation 값이 Zero 일때

• exp와 mantissa가 0이면 값은 0이다.
  $1.0_2\times2^0$ = 0
• Exp = 0이고 Mantissa가 0이아니면 denormalized numbers이다
• Exp = 0xFF, Man = 0이면, 무한대로 판정 e.g) 0으로 나눳을때
• Exp = 0xFF, Man != 0, NaN(Not a Number) e.g) 0/0
  

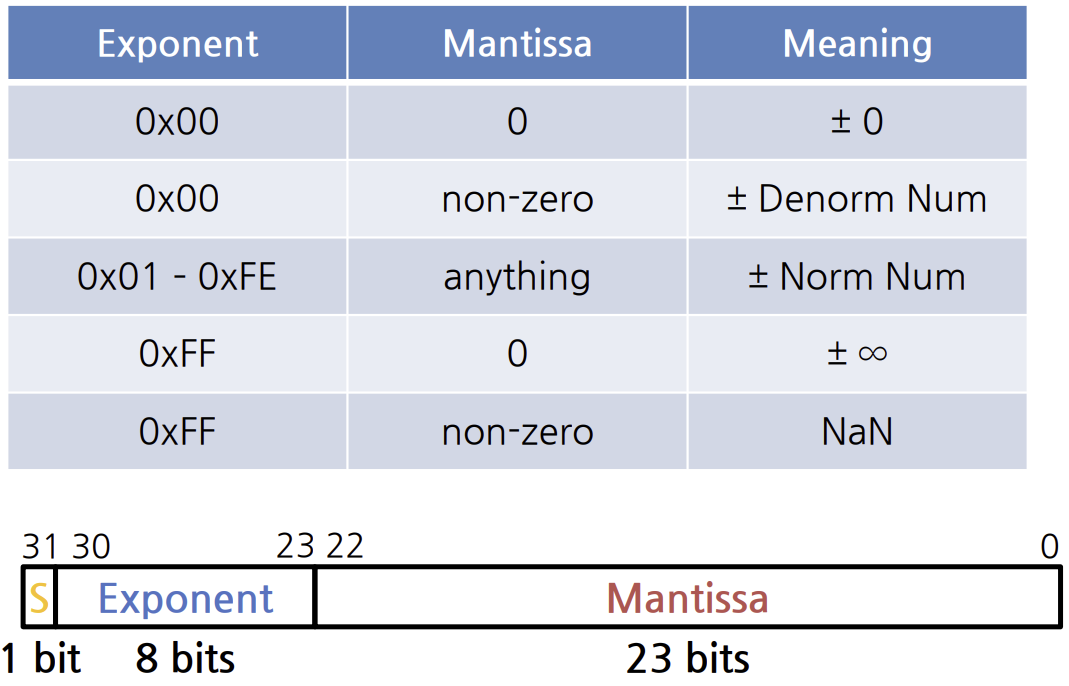
floating point를 decimal로 바꾸기

fp로 변환하기