다항식의 선형 리스트 표현

다항식은 다음과 같이 정리할수 있다.
$A(x) = 4x^3 + 3x^2 +2$는 p1 = ((3,4),(2,3),(0,2)) // (지수,계수)

이것을 1차원 배열로 저장할 수 있다.
$P(X) = a_nX^n + a_{n-1}X^{n-1}+....+a_1X^1+a_0X^0$ 이러한 식이 있다면

$a_n[0]$
$a_{n-1}[1]$
$a_{n-2}[2]$
....
$a_{1}[n-1]$
$a_{0}[n]$

이렇게 1차원 배열로 정리할 수 있다. index 0 에는 제일 큰 차수의 계수를 넣는다. index 1 에는 그다음 차수의 계수를 넣는다.

하지만 만약 $3x^{1000}+x+4$ 이러한 식이 있다면??
지수는 1000이고 배열은 3개만 필요하다. 하지만 배열크기를 1001로 해주어야 하고 공간의 낭비가 큰 희소 다항식이 생성된다.

공간의 낭비를 줄이기 위해 2차배열을 이용한다. <지수,계수> 쌍으로된 2차배열을 만든다.
2차원 배열에서는 행의 개수가 희소 다항식 항의 개수가 된다.

$3x^{1000}+x+4$ 이식은 다음과 같이 2차원 배열로 쓸 수 있다.

1000 [0][0]	3 [0][1]
1 [1][0]	1 [1][1]
0 [2][0]	4 [2][1]

column의 index 0에는 계수, 1에는 차수를 적어준다.

다항식의 덧셈

A

위 방식을 이용해서 다항식의 덧셈을 구해보자.
[addPoly.h]

#pragma once
#define MAX(a,b) ((a>b)? a:b)
#define MAX_DEGREE 50

typedef struct{ 			//구조체 polynominal 정의
	int degree; 			//다항식의 차수를 저장할 변수
    float coef[MAX_DEGREE]; //다항식의 각 항의 계수를 저장할 1차원 배열
}polynomial;

polynomial addPoly(polynomial A,polynomial B);
void printPoly(polynomial P);

[addPoly.c]

#include "addPoly.h"

polynomial addPoly(polynomial A,polynomial B){
	polynomial C; //다항식 덧셈의 결과 다 항식을 저장할 polynomial 구조체 변수 선언
    int A_index=0, B_index=0,C_index=0;
    int A_degree = A.degree,B_degree=B.degree;
    C.degree = MAX(A.degree,B.degree);
    
    while(A_index <=A.degree && B_index <= B.degree){
    	if(A_degree > B_degree){
        	C.coef[C_index++] = A.coef[A_index++];
            A.degree--;
        }
    
    	else if(A_degree == B_degree){
        	C.coef[C_index++] = A.coef[A_index++]+B.coef[B_index++];
            A_degree --;
            B_degree --;
        }
        
        else{
        	C.coef[C_index++] = B.coef[B_index++];
            B.degree--;
        }
    }
    return C; // 다항식 덧셈결과 C를 반환
}

void printPoly(polynomial P){
	int i,degree;
    degree = P.degree;
    
    for(i = 0; i<=P.degree; i++){
    	printf("%3.0fx^%d",P.coef[i],degree--);
        if(i < P.degree) printf(" +");
    }
    printf("\n");
}

[main.c]

#include <stdio.h>
#include "addPoly.h"

int main(void){
	polynomial A = {3, {4,3,5,0}};  // 다항식 A
    polynomial B = {4, {3,1,0,2,1}}; // 다항식B
    polynomial C;
    
    C = addPoly(A,B); // 다항식 C = A+B
    
    printf("\n A(x) ="); printPoly(A); // 다항식A 출력
    printf("\n B(x) ="); printPoly(B); // 다항식B 출력
    printf("\n C(x) ="); printPoly(C); // 다항식C 출력
	getchar(); return 0;
}

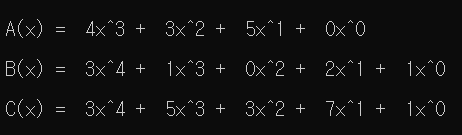
참조

• c로배우는 쉬운 자료구조