선형 리스트 응용 및 구현

행렬의 선형리스트 표현

행렬(matrix)은 행과 열로 구성된 자료구조이다. 행 개수가 m개 , 열개수가 n개이면 m $\times$ n 행렬이라고 한다. 원소 개수는 m $\times$ n 개가 되고, m과 n이 같을때는 정방행렬(square matrix) 이라고 한다.
행과 열을 바꾸어 구성한 행렬은 전치행렬(transposed matrix)라고 한다.
전치 행렬은 만드는 방법은 (i,j) -> (j,i)로 바꾸면 된다.

원소 대부분이 0인 행렬은 희소행렬(sparse matrix)라고 한다.
희소행렬은 실제로 사용하지 않는 공간이 많아 기억 공간의 활용도가 떨어진다.

기억 공간을 좀 더 효율적으로 사용하려면 0이 아닌 값이 있는 원소만 따로 배열로 구성하는 방법을 사용할 수 있다. 예를들어, 0이 아닌 원소들에 대한 <행번호, 열 번호, 값>의 쌍을 구해서 2차원 배열에 저장한다. 이떄 원래의 희소행렬 번호를 저장하기 위해서 <전체 행의 개수, 전체 열의 개수, 0이 아닌 원소의 개수>의 쌍을 첫번쨰 행으로 저장한다.

희소 행렬의 전치연산 구하기

[smTranspose.h]

#pragma once
typedef struct{ //행렬 원소 저장하기 위한 구조체 정의
	int row;
    int col;
    int value;
}term;

void smTranspose(term a[],term b[]);

[smTranspose.c]

#include "smTranspose.h"

void smTranspose(term a[],term b[]){ //a->희소행렬 b->전치행렬
int i,j,p;
b[0].col = a[0].row; 	//전치 행렬 b의 col 수 = 희소행렬 a의 row 수
b[0].row = a[0].col; 	//전치 행렬 b의 row 수 = 희소행렬 a의 column 수
b[0].value = a[0].value; //전치 행렬 b의 원소 수 = 희소행렬에서 0이 아닌 원소 수

if(b[0].value>0){ //0이 아닌 원소가 있는 경우에만 전치 연산 수행
	p=1; //전치행렬 b의 index
    for(i = 0; i<a[0].col; i++) //희소행렬 a의 열별로 전치 반복 수행
    	for(j = 0; j<=a[0].value; j++) // value가 0 이 아닌 값들만 수행
        	if(a[j].col == i){ // 현재의 열에 속하는 원소가 있으면 b[]에 삽입
				b[p].row = a[j].col;
                b[p].col = a[j].row;
                b[p].value = a[j].value;
                p++;
            }
		}
}

[main.c]

#include <stdio.h>
#include "smTranspose.h"

int main(void){
	term a[] = {{8,7,10},{0,2,2},{0,6,12},{1,4,7},{2,0,23},{3,3,31},{4,1,14},{4,5,25},{5,6,6},{6,0,52},{7,4,11}};
    
    term b[sizeof(a)/sizeof(a[0])]; //배열 원소 개수 계산
    int i;
    
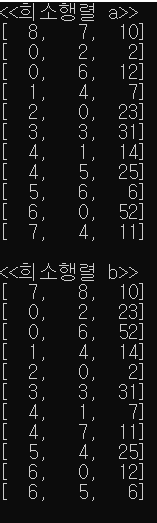
    printf("<<희소행렬 a>>");
    for(i = 0; i<=a[0].value;i++)
    	printf("\n[%3d, %3d, %3d]",a[i].row,a[i].col,a[i].value);
    
    smTranspose(a,b);
    
    printf("\n\n<<희소행렬 b>>");
    for(i = 0; i <= b[0].value; i++)
    	printf("\n[%3d, %3d, %3d]",b[i].row,b[i].col,b[i].value);
        
    getchar(); return 0;
        


}

참조

• c로 배우는 쉬운 자료구조