[알고리즘]Floyd's Alogrithm

Floyd's algorithm

예를들어, 목적지까지 바로가는 항공편이 없다. 무조건 경유를 해야한다.
이때 가장 빠른길로 목적지까지 가는 방법은??

이럴때, 쓸 수 있는게 Floyd's algorithm이다.

그래프에서 vertices를 도시, edge는 거리라고 둔다.

1. path는 그래프에서 인접한 vertices간의 sequence이다.
2. simple path : 한번갔던 vertice를 또 가지 않는다.
3. cyclic path : 마지막 정점이 첫번째 정접과 인접한 simple path이다.
4. 경로의 길이는 경로를 지나는 edge의 weight을 합친 값이다.

• 가장 짧은 경로는 simple path여야만 한다.
• simple path로 가는 길은 여러개가 있을 수 있고, 우리는 그중에서 가장 짤은 경로를 찾아야 한다.
• 모든 정점 쌍에 대해서 둘 사이의 최단 거리를 구할 수 있다.

이 알고리즘은 각 정점에서 모든 정점까지가는 경로의 거리를 모두 구한다.
또한, 더 짧은 거리가 있다면 업데이트 해준다.
예를들어 정점1 --> 정점6 으로 가는데 거리가 10 이었다.
정점1->정점3->정점6 으로 거쳐가는 거리는 8이다.
그러면 원래 10으로 거리가 설정되어 있다가 8로 업데이트 된다.

Floyd's algorithm의 구현 과정

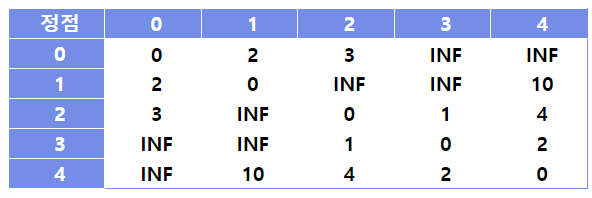
그래프를 배열로 먼저 구현한다.
자기 자신으로 가는 그래프는 0, 연결되어 있지 않은 그래프는 엄청큰수, 연결되어 있는 그래프는 weight의 값을 넣으면 된다.

식은 다음과 같다.

$D[i,j] = min(D[i,j],D[i,k]+D[k,j])$

경유점 k를 지나는 모든 i,j에 대해서 확인한다.

원래 i,j 보다 경유한 i,j가 값이 더 작다면 값을 바꿔준다.

다음예시를 보면 더 잘 이해할 수 있다

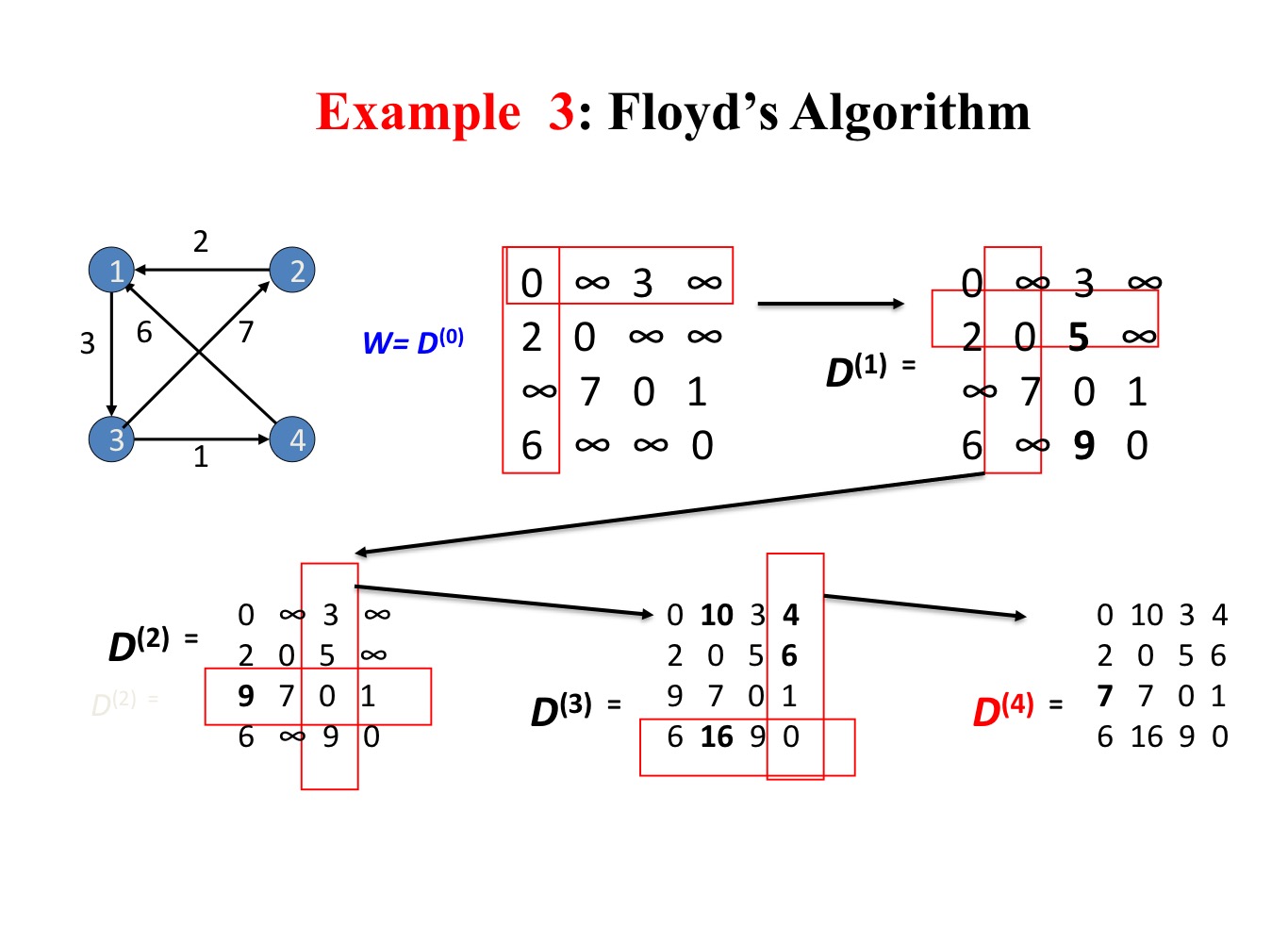
• $D^{(1)}$은 1을 경유로 거쳐갈 경우이다.
• 무한대는 직접적으로 연결되어있지 않은 경우이다

import java.lang.reflect.Array;
import java.util.Arrays;

public class Floyd {
   static int matrix[][];
   final static int INF = 10000000;

    public static void main(String args[]){
        matrix = new int[5][5];
        for(int i = 0; i< 5; i++) {
            matrix[i][i] = 0;
        }
        matrix[0][1] = 2;
        matrix[0][2] = 3;
        matrix[0][3] = INF;
        matrix[0][4] = INF;

        matrix[1][0] = 2;
        matrix[1][2] = INF;
        matrix[1][3] = INF;
        matrix[1][4] = 10;

        matrix[2][0] = 3;
        matrix[2][1] = INF;
        matrix[2][3] = 1;
        matrix[2][4] = 4;

        matrix[3][0] = INF;
        matrix[3][1] = INF;
        matrix[3][2] = 1;
        matrix[3][4] = 2;

        matrix[4][0] = INF;
        matrix[4][1] = 10;
        matrix[4][2] = 4;
        matrix[4][3] = 2;

        floyd(matrix);

        for(int i = 0; i<5; i++)
        System.out.println(Arrays.toString(matrix[i]));
    }

    public static void floyd(int matrix[][]){
        for(int k = 0; k < 5; k++){
            for(int i = 0; i < 5; i++){
                for(int j = 0; j < 5; j++){
                    matrix[i][j] = min(matrix[i][j],matrix[i][k]+matrix[k][j]);

                }
            }
        }
    }

    public static int min(int a,int b){ // 더 작은 값을 리턴한다.
        if(a < b)return a;
        else return b;

    }
}

구현은 생각보다 간단하다.

k라는 정점을 지나는 i->j까지의 경로의 값을 구해서 기존에 있던 i->j까지의 경로보다 짧으면 업데이트 해주면 된다.

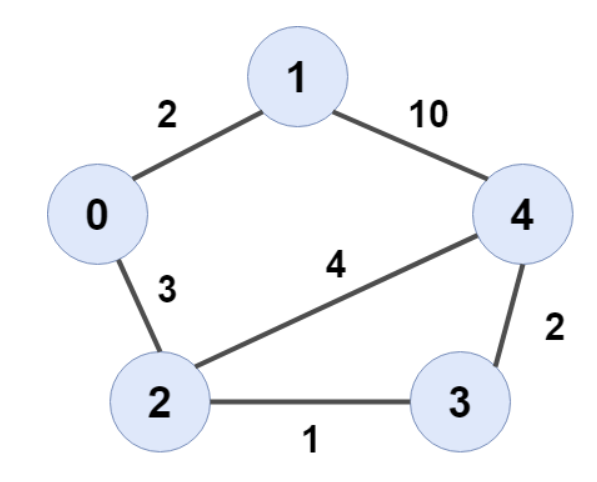
예를들어서, 위 그래프에서

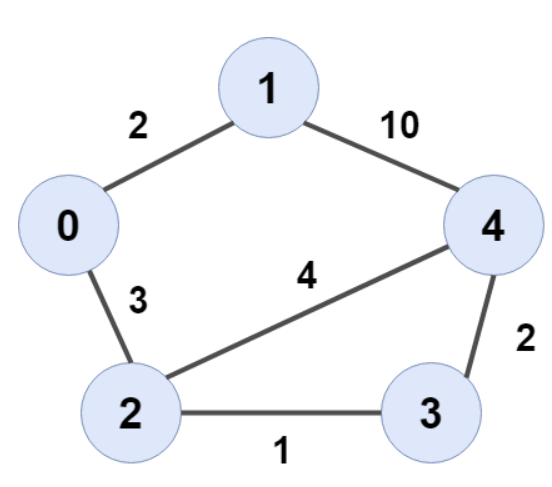
1->3으로 가는 직접적인 경로는 없으므로, 초기에는 INF이다.
순환을 하다가, 1->0->2->3 으로 가는 경로가 가장 짧다는걸 알 수 있다.
코드에서는 min(matrix[i][j],matrix[i][k]+matrix[k][j])로 나타내므로
1->0->2->3을 어떻게 나타내지?? 라고 생각할 수 있지만, 1->0으로 가는 최단경로가 저장되어 있다면 1->2로 가는 경로도 최단거리가 저장되었을 것이고, 1->3까지 가는 최단 거리는 결국 1->2 + 2->3 인것이다.

time complexity

0->n까지의 루프를 3번 하기 때문에, O(n^3)이다.
따라서, 정점이 많은 그래프에서는 사용하기 힘들다. 정점이 100개만 되어도 100만번 수행해야 한다...