[알고리즘]Quicksort

Quicksort

이론

그림으로 보자.

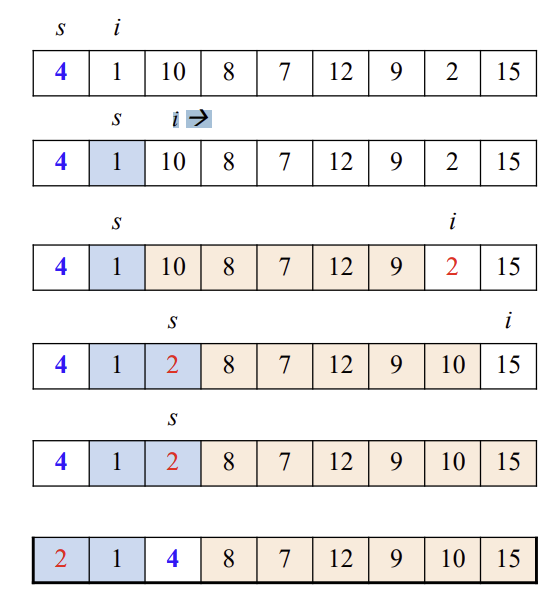
1.pivot(4)을 정한다.(보통 가장 왼쪽의 인덱스)
2.pivot을 제외한 인덱스들중 가장 오른쪽 인덱스에서 부터 왼쪽으로 오면서 pivot보다 작은값 하나와, 가장왼쪽 인덱스로부터 오른쪽으로 가면서 pivot보다 큰 인덱스를 교환해준다.(위 그림에서는 2와10이 된다.)
3.교환을 해주고 교환한 자리에서부터 또 쭉 가다가 교환을 해준다.(다음으로는 없다.)
4.쭉 이어나가다가 크로스가 되었을때, 그 다음으로 만난 피봇보다 작은값과 피봇의 위치를 교환해준다.(4와 2 교환)

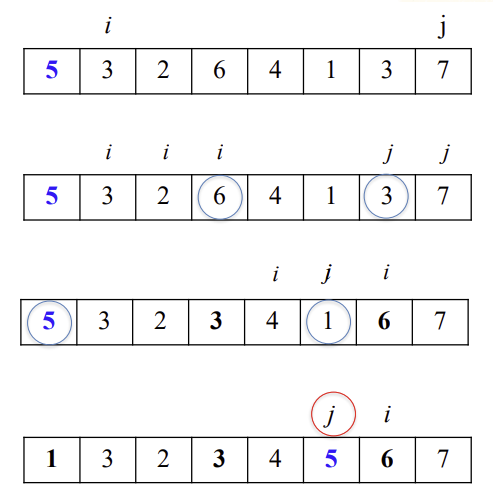
이 그림에서는 교환을 해주다가 j는 1값을 찾았고 i는 j를 넘어간후 값을 찾았다.
따라서 작은값인 j의 값을 피봇과 교환해준다.

pivot의 위치가 이동한 후에는 pivot을 기준으로 배열을 나누어서 앞에와 똑같이 진행한다.

위 그림에서는 [1,3,2,3,4],[6,7]이 될것이다.

시간복잡도

✍️Best case
pivot이 가운데에 있을때는 가장 빠르다
O(nlogn)
✍️worst case
이미 배열이 정렬되어 있는 경우에는 끝까지 순회해야 하기 때문에
O(n^2)
✍️average case
랜덤하게 배열되어 있을 경우에는
O(nlogn)

구현

import java.util.Arrays;


public class QuickSort {
    public static void main(String args[]) {
        int[] arr = {3, 5, 4, 2, 1, 6, 9, 8, 7, 10};
        quickSort(arr, 0, 9);
        System.out.println(Arrays.toString(arr));
    }

    public static void quickSort(int[] A, int start, int end) {
        if(start >= end) return; //배열이 자기 자신 만있는 상태, 바꿀게없다.

        int pivot = start;
        int i = pivot+1;
        int j = end;

        // 엇갈리기  전까지 반복
        while (j >= i) {
            while (A[pivot] >= A[i] && i <= end) i++;
            while (A[pivot] <= A[j] && j > start) j--;
            if(j < i ){ // 엇갈린 상태면 pivot값과 교체
                swap(A, pivot, j);
            }else { 
                swap(A, i, j);
            }
        }
        quickSort(A, start, j - 1);
        quickSort(A,  j+1, end);
    }
    public static void swap(int[] A, int a, int b) { 
        int tmp = A[a];
        A[a] = A[b];
        A[b] = tmp;
    }
}

다맞는것 같은데 stackoverflow가 계속 나길래, 확인해보니
while (A[pivot] <= A[j] && j >= start) j--;
이거였다..
start == j인 상태에서도 루프가 돌기 때문에 j-- 되면 stackoverflow가 되는것이었다...

그래서 이렇게 고쳤다.
while (A[pivot] <= A[j] && j > start) j--;

quickSort는 정렬되어 있지않은 상태에서는 빠르지만(O(nlogn)), 정렬되어 있는 경우 오래걸리기 때문에 쓰지 않는다.(O(n^2))