[GTL] Epic (06/12) - 배경지식

brights2ella·2025년 6월 16일

게임테크랩 음향 정글

정글게임테크랩1기

목록 보기

7/14

소리

진폭

파동 변위( $y$ )의 최대 크기

파장과 주파수

파장은 마루와 마루 사이 (또는 골과 골 사이), 한 주기 파동의 길이.
주파수(진동수)는 파장의 역수.

위상

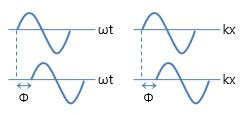
파동 한 주기 내부에서의 위치. 각도로 나타낸다.

소리의 물리량

음향 파워

소리 강도를 나타내는 기본적인 물리량이다. 단위는 $\text{W}$ .

음향 파워 레벨 (PWL)

음향 파워의 기준값에 대한 비율을 로그스케일로 나타낸 것이다.

L_W = 10\log_{10}({W\over W_{ref}})

이때 $W_{ref} = 10^{-12}\text{W}$ 이다.

음향 인텐시티

단위면적당 소리 강도를 나타내는 물리량이다. 단위는 $\text{W/m}^2$ .

음향 인텐시티 레벨

음향 인텐시티의 기준값에 대한 비율을 로그스케일로 나타낸 것이다.

L_I = 10\log_{10}({I\over I_{ref}})

이때 $I_{ref} = 10^{-12}\text{W/m}^2$ 이다.

음압

매질의 압력에서 평균 압력을 뺀 것. 만약 매질이 공기라면, 특정 부분의 대기압에서 평균 대기압을 뺀 것을 말한다.

p = p_t - p_0

단위는 $\mu \text{Pa}$ .

음압 레벨 (SPL)

음압과 기준 음압의 제곱 비율을 로그스케일로 나타낸 것이다. 이때 음압은 실효값을 쓴다.

L_p = 10\log_{10}({ p_{rms}^2 \over p_{ref}^2}) = 20\log_{10}({ p_{rms} \over p_{ref}})

이때 대기중에서 $p_{ref} = 20 \mu \text{Pa}$ 으로 $1\text{kHz}$ 에서의 최소 가청치를 기준으로 했다고 한다. 단위는 $\text{dB}$ .

참고
참고: Master Handbook of Acoustic. 5th Edition.

실효값 (RMS)

파동 한 주기의 제곱평균제곱근 값으로 파동의 크기를 나타내기 위해 쓰인다. 정확힌 아래와 같다.

x_{rms} = \sqrt{{1\over T} \int^T_0 f(t)^2dt}

정현파의 경우 진폭의 $1\over\sqrt{2}$ 배와 같다.

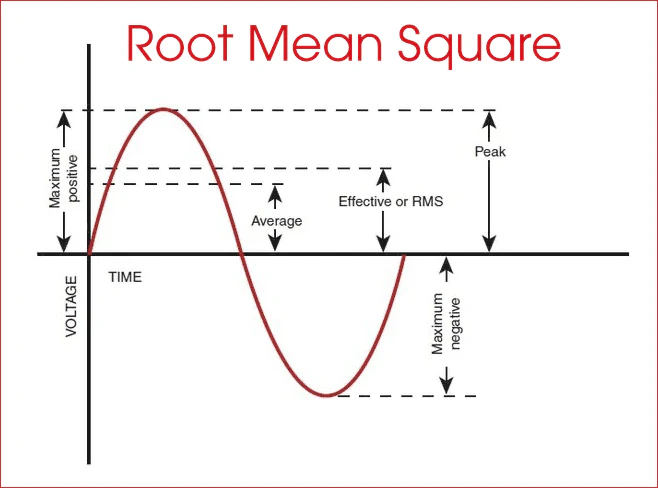
통계적으로 나타내면 다음과도 같다.

x_{rms} = \sqrt{E[x^2]}

만약 파동 한 주기의 평균이 0이라면, RMS는 파동의 표준편차와 같다고 생각할 수도 있다.

x_{rms} = \sqrt{E[x^2-\mu]} = \sigma_x \quad (\mu = 0)

소리의 디지털 표현

PCM

소리 신호를 디지털로 나타낸 것. .wav, .aiff 등의 파일 포맷이 이를 사용한다.

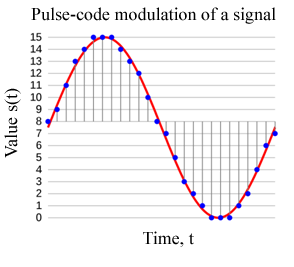
이때 PCM의 x축은 시간을, y축은 소리에서 음압을 나타낸다.

각 축의 해상도는 Sample rate, Bit Depth에 따라 달라진다.

Sample Rate

PCM 하나의 데이터를 Sample이라고 부르며, Sample Rate는 1초에 몇 개의 Sample이 재생되는지를 의미한다. 보통 44100hz이다. (1초에 44100개의 샘플이 재생)

PCM에서 x축의 해상도라고 생각하면 된다.

Bit Depth

Sample 하나를 표현하는 데 몇 비트가 사용되는지를 의미한다. 보통 16bit로 65536단계(-32768~32767)를 표현할 수 있다.

PCM에서 y축의 해상도라고 생각하면 된다.

소리의 합성

소리의 합성은 두 파동(PCM)을 단순히 더하는 것으로 이루어진다. 그러나 합성된 소리의 크기는 두 파동의 파형에 따라 달라진다.

어떤 두 소리를 더해서 나온 소리의 크기(RMS)는 다음과 같다.

y_{rms} = \sqrt{x_{1_{rms}}^2 + x_{2_{rms}}^2 + 2 \cdot \text{Cov}(x_1, x_2)}

이때 $\text{Cov}(x_1, x_2)$ 는 공분산으로 상관계수 $\rho_{x_1x_2}$ 에 대해 다음과 같으며, 각 $\sigma$ 는 RMS로도 해석할 수 있다.

\text{Cov}(x_1, x_2) = \rho_{x_1x_2} \cdot \sigma_{x_1} \cdot \sigma_{x_2}

동일한 파형

같은 소리에 위상만 다르다면 $\text{Cov}(x_1, x_2)$ 가 값을 가지게 된다. 소리가 같으므로 RMS 역시 같으며, 상관계수의 범위는 $-1 \le \rho_{x_1 x_2} \le 1$ 이므로 아래와 같다.

y_{rms} = \sqrt{2x_{rms}^2 + 2\rho_{x_1 x_2}x_{rms}^2} \\ 0 \le y_{rms} \le 2x_{rms}

$0$ 인 경우 완전한 상쇄 간섭, $2x_{rms}$ 인 경우 완전한 보강 간섭이 나타남을 의미한다.

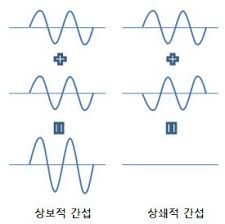
이때 $y_{rms} = 2x_{rms}$ 라면 음압 레벨 식에 따라

L_p = 20\log_{10}({ y_{rms} \over x_{rms} }) = 20\log_{10}(2) = 6.02...

이므로 기존 소리에 비해 6.02dB이 커진다.

비상관 파형

서로 다른 두 소리라면 $\text{Cov}(x_1, x_2) \approx 0$ 이므로

y_{rms} = \sqrt{x_{1_{rms}}^2 + x_{2_{rms}}^2}

만약 두 신호의 RMS가 같다면

y_{rms} = \sqrt{2x_{rms}^2} = \sqrt{2} x_{rms}

음압 레벨 식에 따라

L_p = 20\log_{10}({ y_{rms} \over x_{rms} }) = 20\log_{10}(\sqrt{2}) = 3.01...

이므로 기존 소리에 비해 3.01dB이 커진다.

brights2ella

다음 포스트