Gradient Boosting에 관하여…
Background-Gradient Boosting
부스팅의원리
A식에 관한 설명
먼저 t 시점에서 현재 모델 Ft가 있다.
Ft가 예측하지 못한 것에 대해 추가로 예측한 어떤 h중에
두 모델에 의한 예측값의 합과, 실제값 y의 로스를 최소화 시키는 H를 Ht+1로 만들어 준다.
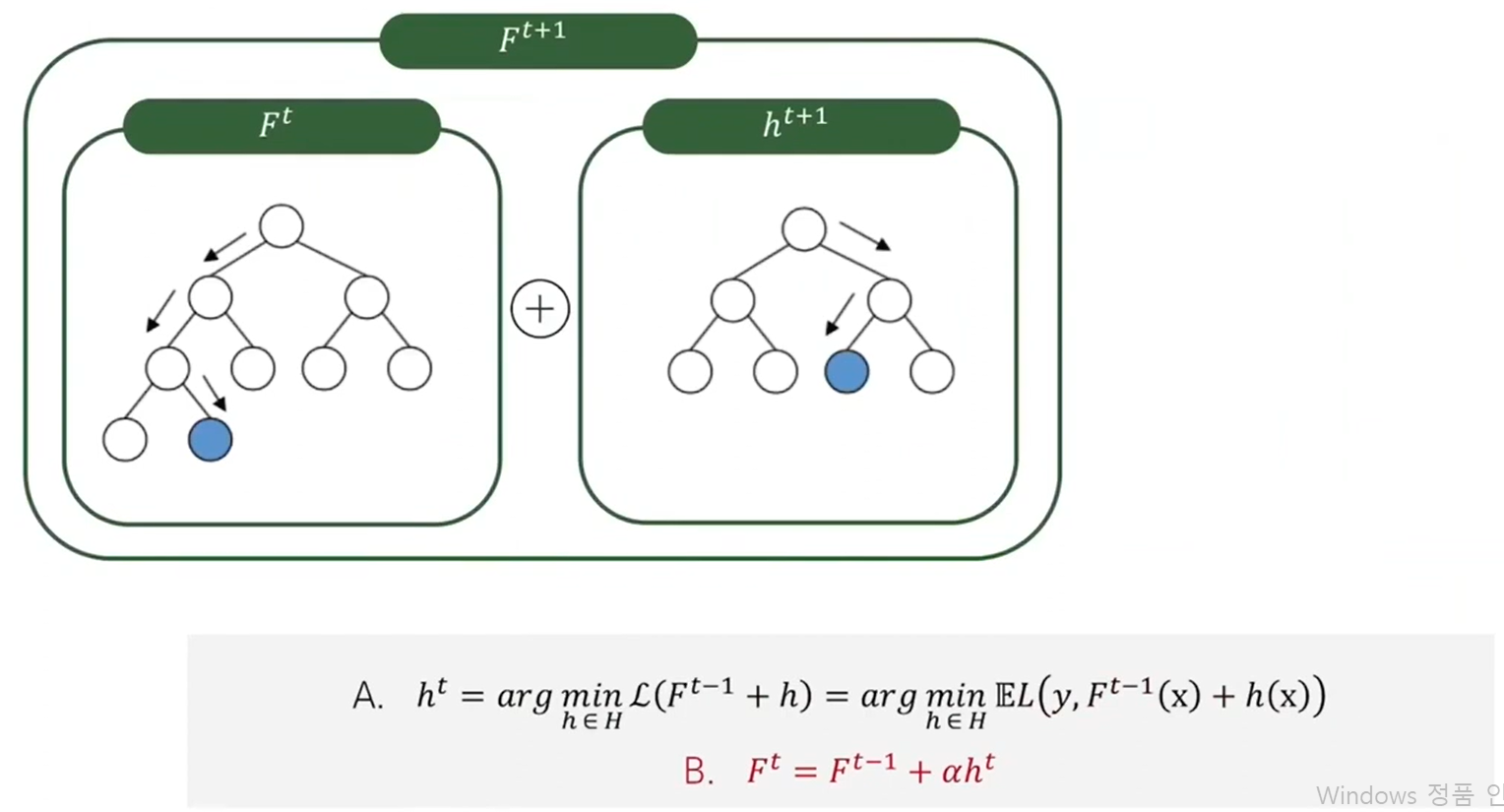
Ft에 Ht+1을 스텝사이즈 알파만큼 더해, t+1시점의 모델 Ft+1이 만들어 졌다.
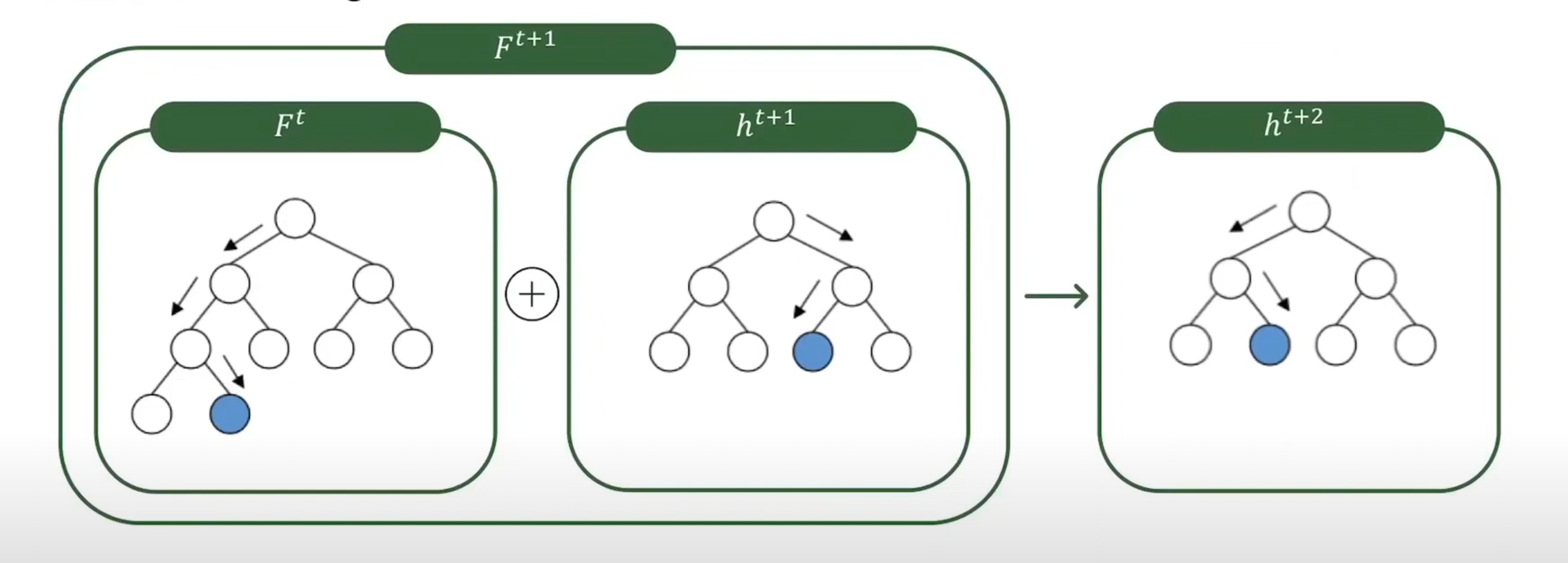
그 다음에 이 과정을 반복한다.
실제값과 모델의 로스를 최소한으로 시키는 h를 구하고 현재 모델인 ht+2를 결합해 Ft+2를 구한다.
Loss function에대한 minimalize 문제
경사하강법으로 해결 가능
Loss function을 Ft-1 (X)로 미분한 Gradient의 음수값 Negative Gradient는 Loss function의 값이 작아지도록 Ft-1(x)가 가려는 방향이다.

따라서 1번식과 같이 이 Negative Gradient를 가장 잘 예측하는 H(x)를 H(t)로 선택해야한다.
Gradientboosting을 각 단계의 Residual을 예측하여 전체 Loss를 줄이는 알고리즘이라고 하는데, 그 이유가 3,4번 식에 나와있다.
3번식과 같이 Loss Function으로 Squared Error을 쓰는 경우 Loss function의 Negative Gradient는 Residual의 의미를 갖는다.
따라서 각 단계에서 Gradient를 근사한 h를 찾는 Gradient Boosting은 Residual을 예측하는 H를 찾는 과정이라고 말할 수 있다.
Residual이란?
Gradient Boosting에서 사용되는 손실 함수(Loss function)로 Squared Error를 선택한 경우, 각각의 트리는 모델이 현재까지 학습한 예측과 실제값 사이의 잔차(residual)를 학습하려고 노력합니다.
여기서 잔차는 각 데이터 포인트에 대한 현재 예측값과 실제값 사이의 차이를 나타냅니다. 예를 들어, 특정 데이터 포인트의 실제값이 10이고 현재 모델의 예측값이 7이라면, 이 데이터 포인트의 잔차는 10 - 7 = 3이 됩니다.
Gradient Boosting은 이러한 잔차에 대한 트리를 순차적으로 학습시켜 나가는 방식으로 작동합니다. 각 트리는 이전 트리가 만든 예측에 대한 잔차를 학습하려고 하며, 이렇게 계속해서 잔차를 줄이는 방향으로 모델이 학습됩니다. 이것이 Gradient Boosting에서 "Gradient"이라는 용어가 나오는 이유입니다. 잔차의 그래디언트(기울기)를 최소화하려고 하는 것이기 때문입니다.
따라서 Squared Error를 사용할 때, 각 트리는 이전 트리의 예측값과 실제값 사이의 잔차를 학습하며, 이를 통해 전체 모델의 예측 성능을 향상시킵니다.
Statistical Issue
Catboost 이전에 존재하던 Gradient Boosting 기법들은 몇가지 Statistical Issue를 가지고 있었다.
- Statistical Issue 1
NG(Negative Gradient)를 근사한 H를 찾기위해 실제 X,y에 대한 NG와 H차이에 대한 Expectation이 필요한데, 그 때 모든 가능한 X와 Y를 가지고 있지 않기 때문에, 이 기대값을 보통 이미 가지고 있는 Train Data를 이용하여 추정하게 된다.

그 때, 각각의 단계에서 Gradient를 구할 때 매번 같은 Train data만 사용하기 때문에 이것만 학습하게 되고, 이로 인해 구해진 F(X.k)는 실제 test data가 주어졌을 때, F(x)와 같은 분포를 가지지 않을 수 있게 된다.
이를 X가 training example일때 CD(conditional distributin)가, X가 test example일때 CD으로부터 Shifted 된다고 표현했고, 이것을 Prediction Shift로 정의했다.
이를 해결하기위해 Ordered Boosting이라는 방안을 제시했다.
- Statistical Issue 2
두 번째 이슈는 Categorical Features를 Preprocessing하는데 있습니다.
이게 원핫으로 하면 ㅈㄴ 많으니까, Target Stastic으로 대체해서 Numerical 취급 가능하게 만들어 주었음
TS(Target Statistic)= 같은 카테고리에 속한 instance들의 target값의 평균
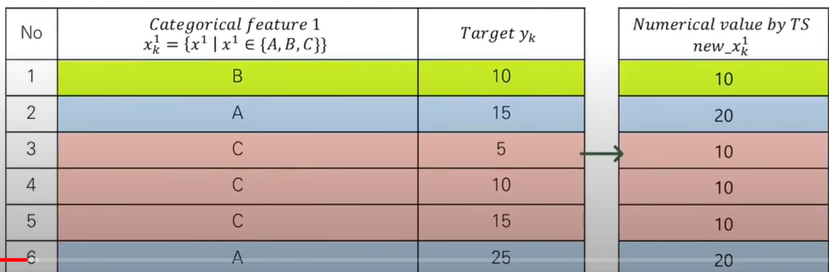
예측값을 만드는 그 시점에 알 수 없는 데이터를 포함하고 있을 때, 일어나는 Data leakage 문제가 있음.
이 논문은 두 가지를 해결하기 위해 Ordering Principle를 제안하고 있다.
이 원리를 기반으로 orderdboosting으로 Prediction shift 를 피하고, Orederd Ts 적용해 Dataleakage를 피한다.
Catboost!!!
Target Statistic
Categroy에 속하는 모든 instance들의 target값의 기대값으로 categorical feature 로 대체한다.

TS계산에 어떤 dataset을 쓰냐에 따라 Greedy TS, Holdout TS로 나뉜다.
Greedy TS
가장 단순한 방법.
같은 카테고리에 속하는 instance를 Target y값으로 평균해 추정을 하는데,
낮은 빈도로 나타는 카테가리를 noise를 추정함을 막기 위해 smoothing을 해준다.
여기서 p는, 전체 데이터 셋의 target y average를 사용한다.
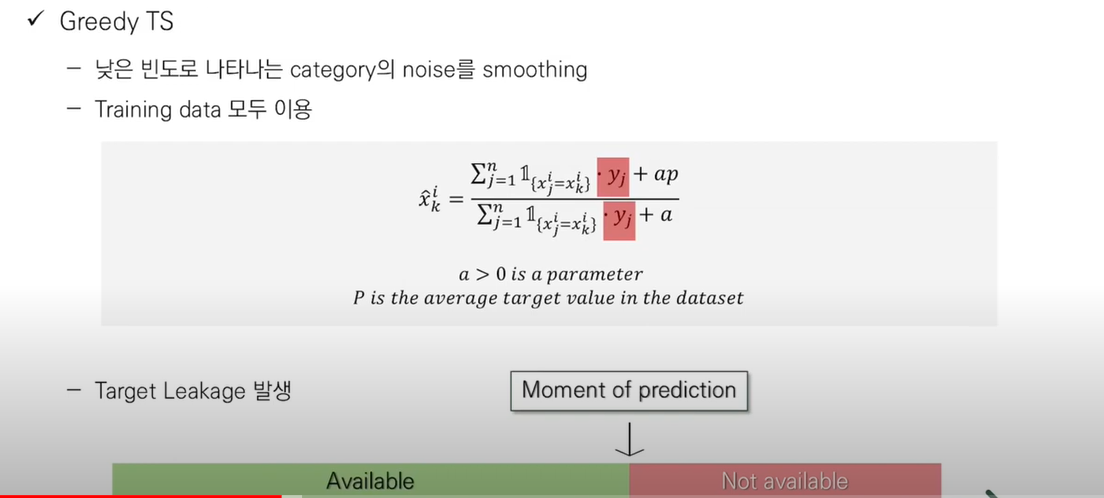
이러한 방식의 문제점은 Targert Leakage이다.
특정 카테고리에 속하는 Xk를 추정하기 위해선, Xk를 포함한 모든 카테고리 변수들의 타깃값인 Yk의 평균값을 사용하는데, 이는 모델을 학습할 때 알 수 없는 정보이기 때문에, Data leakage가 발생합니다.
따라서 y값 없이 주어졌을때, X의 categorical feature i에 대한 y값들은 train data에만 개선되었기 떄문에, test set이 가지는 분포는 이와 다를 수 있다.
이러한 점은 모델에 있어 training 데이터의 overfiting을 야기하기 떄문에, (제너럴레이션)Error에 매우 큰 영향을 준다.
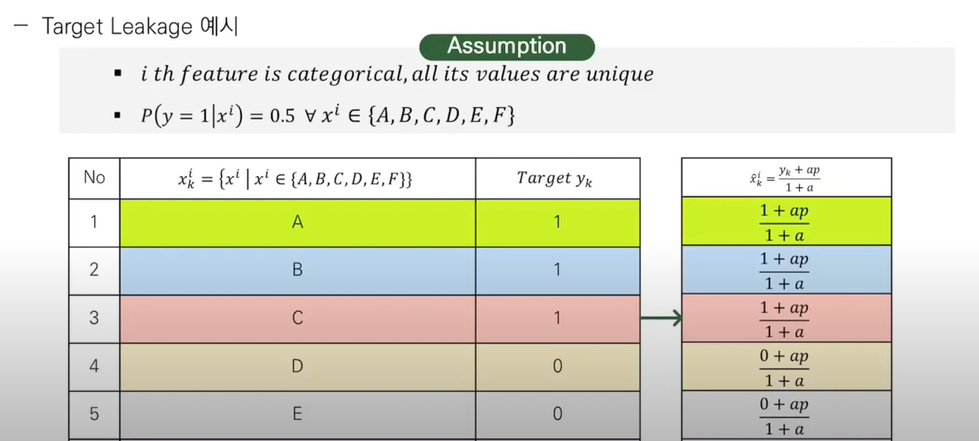

위에는 그에 대한 예시이다. 각각의 개별적인 분포를 가지는 데이터들이 있다고 하자.
1이 될 target확률이 0.5라고 한다면, 각각의 greedy 식에 의해 모두 0.5가 되고,
그럼 Threshold가 0.5로 설정되고, ⇒ t = 0.5+ap/1+a 모든 train을 완벽하게 분류할 수 있게 된다.
하지만 test instance는 0.5보다 크면 1, 아니면 0으로 분류하게 된다.
여기서 tareget leakage가 발생, prediction shift 발생하게 된다.
Property
이런 문제를 피하기 위해 TS에대한 Property를 정의한다.
Property 1
모든 training example에 대한 Target 값이 같을 때,
Training instance에 대한 TS기대값과, Test instance에대한 TS기대값이 같아야 함을 의미한다.
Greedy Ts는 이러한 성질을 만족시키지 못하였다.
이런 Conditional distribution이 다른 Prediction shift를 피하는 방법중에 가장 일반적인 아이디어는,
Xk를 제외한 subset Dk로부터 구하는 것이다.
Xk의 TS를 계산하는데 자기 자신을 쓰지 않게 하는 방법 중 하나는, 데이터셋을 두 부분으로 나눠 하나의 Subset은 TS를 계산하는데, 나머지는 계산된 TS를 가지고, Training하는데 쓰는 것이다.

이 방법은 Property1을 만족하지만, TS를 계산할수 있는 데이터와 트레이닝에 쓰이는 데이터의 양이 크게 줄기 때문에 데이터를 최대한 사용할 수 없다는 단점이 있다.
따라서 TS에게 요구되는 두 번째 Property 2를 다음과 같이 정의한다.
Property 2.
Effective usage of all training data for calculating TS features and for learning a model.
모델을 Training하고 TS를 계산하는데 Trainingdata 를 효율적으로 사용해야한다.
Leave - one - out - TS
TS를 계산할 때 Dk(Xk를 제외한 subset)을 사용하고, Test의 TS를 계산하는데에는 Train 데이터셋 전체를 사용하는 방법.
instance 하나씩 빼고 TS와 Training이 이루어져, Property 2 만족.
이 방법도, greedy처럼 Train은 완벽하게 분류할 수 있지만 Test를 완벽하게 분류할 수 없을 가능성이 있다.
따라서 Property 1 불만족.
OrderedTS & OrderedBoosting
OrderedTS
이 방법은 train을 시간에 따라 순서대로 가져오는 Online learning 알고리즘에서 착안 되었다.
각각의 instance에 대한 TS값이 현 시점에서 이미 관측된 History에서만 계산 되는 것이다.

이 아이디어를 시간 개념 없는 Offline세팅에 적용하기 위해 Random permutation 시그마를 인공 시간으로 도입했다.
데이터셋에 임의의 시간 값 (random permutation)을 부여하고, k번 째 데이터의 TS를 계산할 때, k−1
번까지 데이터의 target value만을 사용하는 것이다. 이를 통해 target leakage를 방지할 수 있다. 또한 모든 데이터셋을 학습에 사용할 수 있기 때문에 Property 1, 2를 모두 만족한다. CatBoost에서는 이 Ordered TS 방법을 활용한다.
이떄 gredient Boosting을 하는동안, 같은 순열 하나만 사용한다면 이 순열에서 앞에 있는 인스턴스들은 TS를 계싼할 때 사용하는 데이터수가 적기 때문에 TS의 분산이 뒤에있는 instance 분산들보다 커지게 된다. 따라서 catboost는 각각의 Boosting Step에서 각기 다른 랜덤 순열을 생성해서 사용한다.
CatBoost:OrderdBoosting
각 Boosting 단계에서 학습에 사용되는 Dataset은 independent 해야한다.
각 Boosting 단계에서 gradient 계산시, Ft를 training하는데 쓰인 dataset과 independent dataset을 사용함으로써 prediction shift를 피할 수 있다.
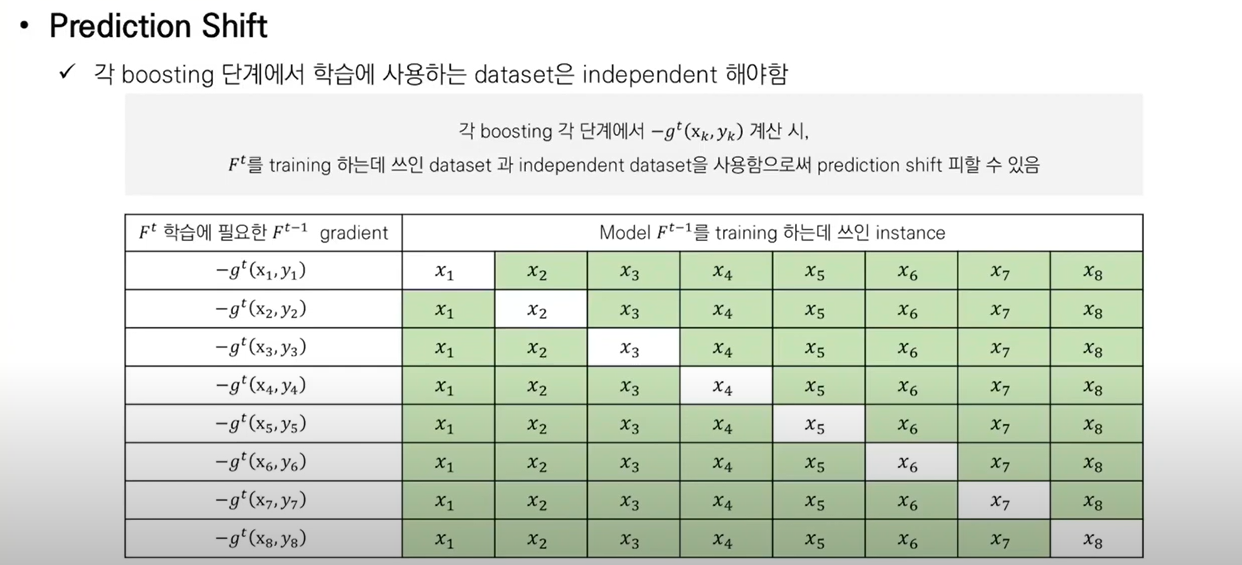
Prediction shift의 원인이 되는 target leakage를 방지하기 위해서 CatBoost는 트리를 학습하는 매 스텝마다 다른 데이터셋 (independent samples) 을 활용해야 한다고 말합니다.
Training이 사용된 instance에 따라 Model의 집합을 다르게 유지하면, 각 단계에서 독립적인 데이터 셋을 사용하는 것이 가능하게 된다.
논문에서 원하고 있는 Orederd Boosting이 이 방법이다.
이를 위해! OrderedTS에서 설명했던, Random Permutation이 도입된다!
M.i는 train이 instance들의 순열에서 먼저 위치한 instance만을 가지고 만들어진 모델을 뜻한다.
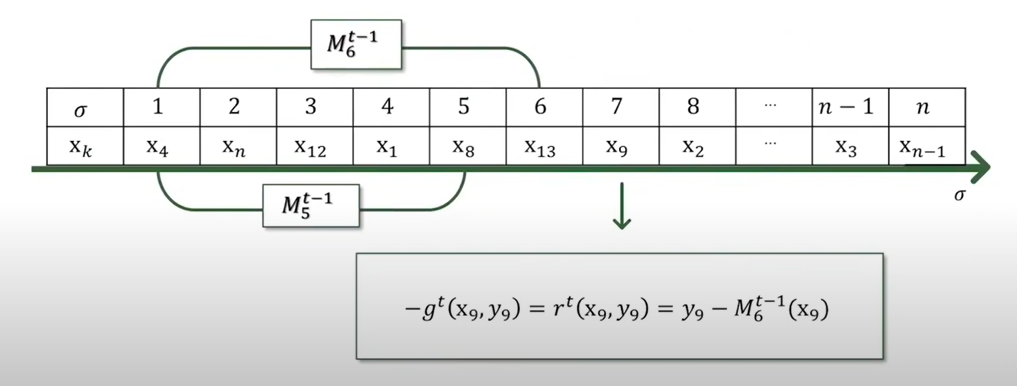
j번째 인스턴스들의 Residual을 얻기위해 모델 M.j-2를 사용한다.
이러한 방법을 Orederd Boosting라고 한다.

T시점의 모델을 구하기 위해 필요한 X9에 대한 Residual을 구하기 위해서는, 순열상에서 X9가 위치한 7번의 앞쪽에 있는 데이터들로 트레이닝된 모델 M.6t-1로부터 그래디언트를 구하게 된다.
모델 M5와 M6도 이와 마찬가지로 학습된 모델이다.
Algorithm
Algorithm 1
자자 이를 정리하면!

input으로 train instance와 Boosting step i가 들어오고 입력된 trianing instance에서 [1,n]까지 랜덤 순열을 부여하고, N개의 모델 M을 초기화 해준다.
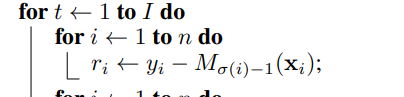
이제 이 시점부터 Boosting이 끝나는 시점 i까지 Residual을 구하고 모델을 학습하는 것을 반복한다.
우선 모든 train instance n개에 대해 Residual r.i를 구하는데
이때, r.i는 Train instance의 무작위 순열에서 Xi의 위치 시그마 i의 바로 앞까지의 instance들로 trianing한 M시그마(i)-1로 Residual을 구한다.
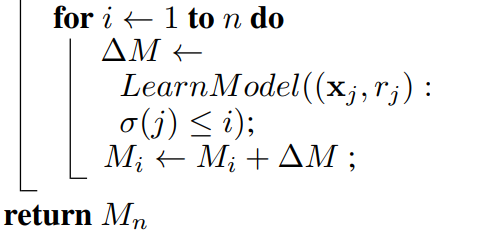
이렇게 구한 Residual중 무작위 순열 시그마에서 Xi앞의 instance의 Residual만 가지고 M.i를 업데이트 시킨다.
이렇게 되면 각각의 instance의 Residual을 구하고 모델을 업데이트 할 때 독립적인 Dataset을 사용하므로 Prediction의 bias가 일어나지 않게 된다.
이 논문에서 제시한 Orederd Boosting과 Ordered TS 둘 다 무작위 순열(Random Permutation)을 사용하는데, 이 두가지 방식을 하나로 합칠 때 같은 순열을 사용하도록 설정해주고 있다.
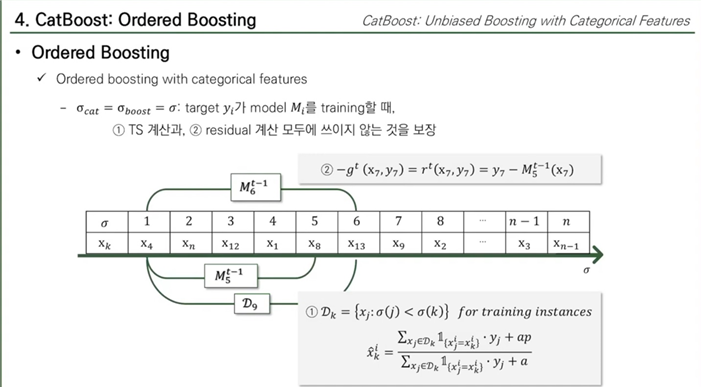
이는 Target y.i가 model Mi를 training 할 때, TS계산과 Residual 계산 모두에 쓰이지 않는 것을 보장한다.
Practical Implementaion
이제 Catboost에서 어떻게 구현 되는지 알아보도록 합시다.
얘는, 두 가지로 구분 된다.
- Plain Mode
GBDT와 같은 알고리즘을 사용함.
But, Categorical feature들만 Ordered TS만 사용하는 것이다.
- Ordered Mode
Ordered Boosting, Ordered TS 사용
Base Predictor
CatBoost는 트리를 구성할 때 oblivious decision tree (ODT) 로 구성합니다. ODT는 아래 이미지처럼 트리의 level 마다 동일한 조건을 부여하여 좌우대칭의 형태로 만든 decision tree이다.
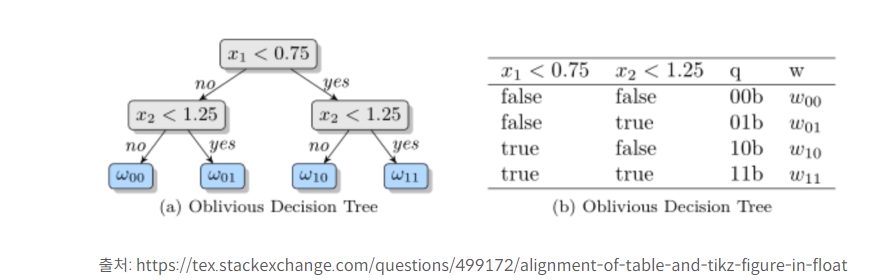
오버피팅 가능성을 줄여주고, 학습된 모델로부터 테스팅을 수행할 때 소요되는 시간을 줄여준다고 합니다.
Algorithm2
Tree의 Algorithm
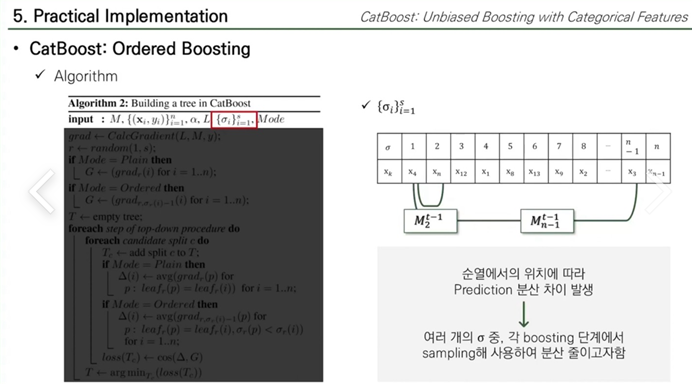
CatBoost는 트레이닝 데이터의 S+1개의 independent한 무작위 순열을 만다.
만약 하나의 Random Estimate를 쓴다면,
앞쪽의 Xi를 고르면 표본의 수가 적어지므로 분산이 커짐 → Predict 값도 커진다.
그래서 여러개의 시그마를 쓰면서 분산을 줄이고자 한다.
⇒ 여러개 쓰면서 분산을 줄이려고 각 iteration마다 [1,s]개중에 시그마 하나를 Sampling
이를 바탕으로 Tree를 만들게 된다.

또한, Boosting이 시작되기 전에 Categoricla Feature을 시그마에 따른 Orederd Ts로 대체한다.
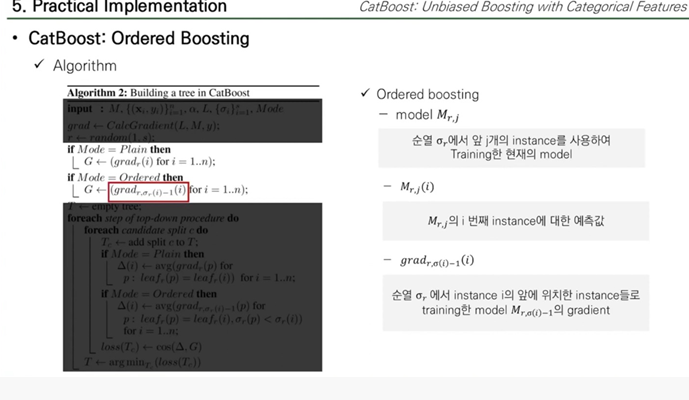
plain은 데이터셋에 구분을 두지 않기 때문에, 그냥 Gradient Boosting을 한다.
Orederd는 독립적인 데이터셋을 유지하기 위해 M.r.j를 만들고 나서 그 다음 시점에 Tree를 만들기 위해 모든 instance n에 대한 grad.r.(i)-1(i)를 계싼하여 저장한다.
→ grad.r.(i)-1(i)의 의미는 무작위 순열 시그마 R에서 i-1까지 즉, 인스턴스 i 바로 전까지, M.i-1(instance들로 학습한 모델 )의 Gradient를 뜻한다
여기선 Gradient는 Cosine similarity로 사용한다.
이제 Tree를 만들기 위해 최적의 Split을 학습해야 한다.

leaf.r.(i)는 그 단계에서 선택된 순열 시그마r에 Dependent한다.
왜냐면 시그마R은 instance i 의 Orederd TS값에 영향을 줄 수 있기 떄문이다.
이렇게 후보 split을 loss를 minimize하는 split을 선택하는 것을 반복하여 Tree structure(T)만든다.
이렇게 Tree structure가 t가 만들어지면 이 tree를 사용해 모든 모델 M.r.j를 Boosting 하는데 사용한다.

기존 Gradient Boosting DT와 다른점은,
training data에 categorical feature가 있다면, s개 무작위 순열에 기반해 categorical feature를 Ordered TS로 대체 후 학습한 s개의 model M.r 을 생성하는게 기존의 GB와 구분된다.
