통계적으로 추론하기
가설검정, 순열검정
모수검정
모집단에 대한 파라미터를 추정하는 방법을 의미하며, 파라미터는 평균, 분산을 의미하며 모집단은 관심 대상이 되는 전체 데이터를 의미한다. 예로 청소년의 몸무게 평균을 알고싶다면 전체 청소년이 모집단이 된다.
모수검정은 모집단의 데이터에 대해 어떤 가정을 전제로 하고 수행되는 경우가 많으며 예로 전체 청소년의 몸무게가 정규분포를 따른다고 가정한다. 실제로 전체 데이터는 알지 못하지만 대부분의 데이터는 정규분포를 따르는 경우가 많기 때문이다.
표본점수
데이터가 정규분포를 따른다고 가정하고, 각 값이 평균에서 얼마나 떨어져 있는지 표준편차를 사용해 변환한 점수를 표준점수 또는 z점수 라고한다. 평균까지의 거리를 표준편차로 나눈것을 z점수라고 함
Z 점수 구하기
- 넘파이
# 7에대한 점수 구하기 import numpy as np x = [0, 3, 5, 7, 10] s = np.std(x) m = np.mean(x) z = (7 - m) / s print(z) #출력 0.5872202195147035 - 사이파이
from scipy import stats stats.zscore(x) #출력 array([-1.46805055, -0.58722022, 0. , 0.58722022, 1.46805055])
누적분포 이해하기
평균이 0이고 표준편차가 1인 정규분포를 표준정규분포라고 한다.
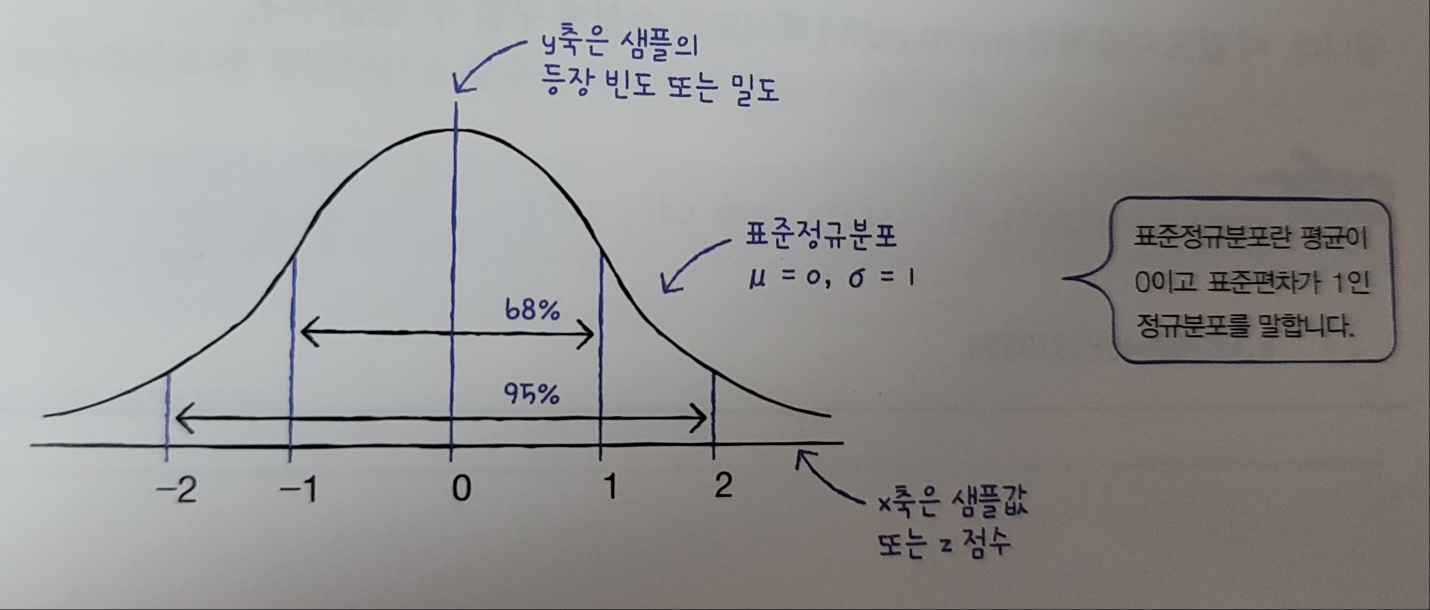
누적분포 구하기 : norm.cdf() 메서드
사이파이함수의 norm.cdf()메서드를 이용하여 누적된 분포를 구할수있다.
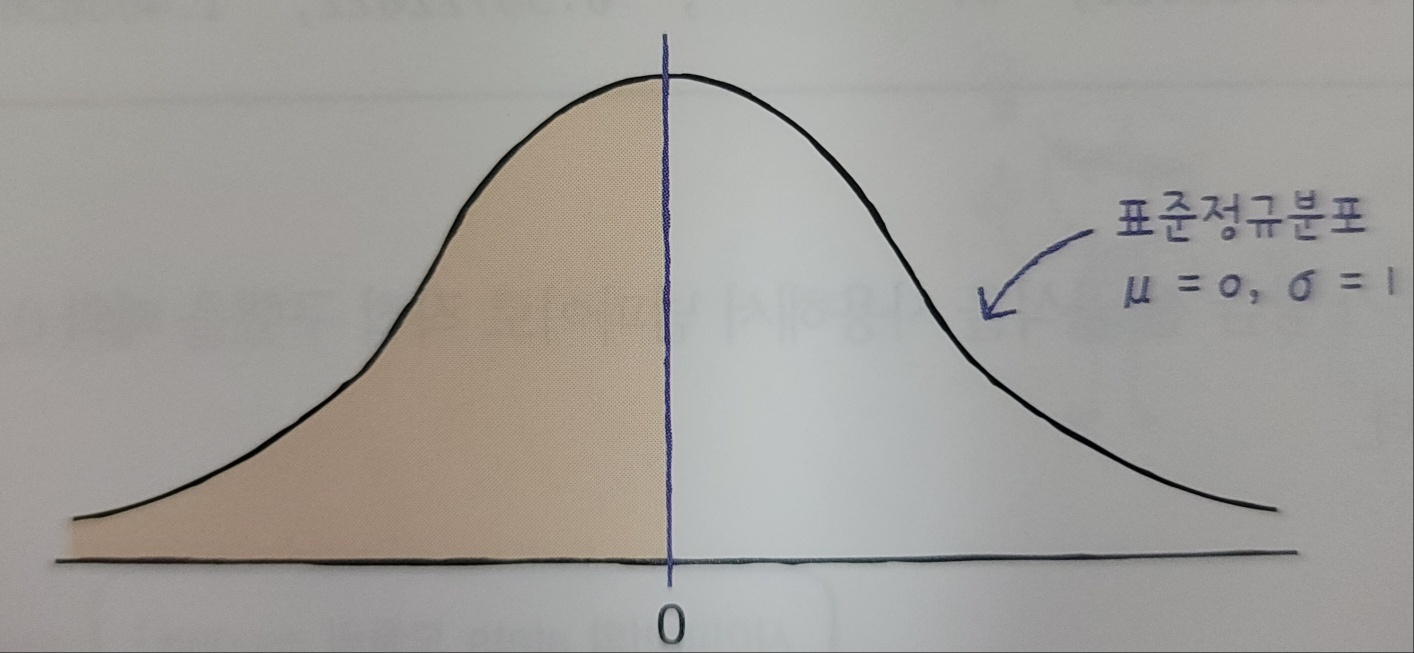
# 평균 0을 전달하여 0까지의 비율 구하기
stats.norm.cdf(0)
#출력
0.5
# 1이내 비율, 1까지의 누적분포에서 -1의 누적분포를 빼면됨
stats.norm.cdf(1) - stats.norm.cdf(-1)
# 출력
0.6826894921370859
# 90% 누적분포의 해당하는 z점수
stats.norm.ppf(0.9)
# 출력
1.2815515655446004중심극한정리
무작위로 샘플을 뽑아 만든 표본의 평균은 정규분포에 가깝다라는 이론
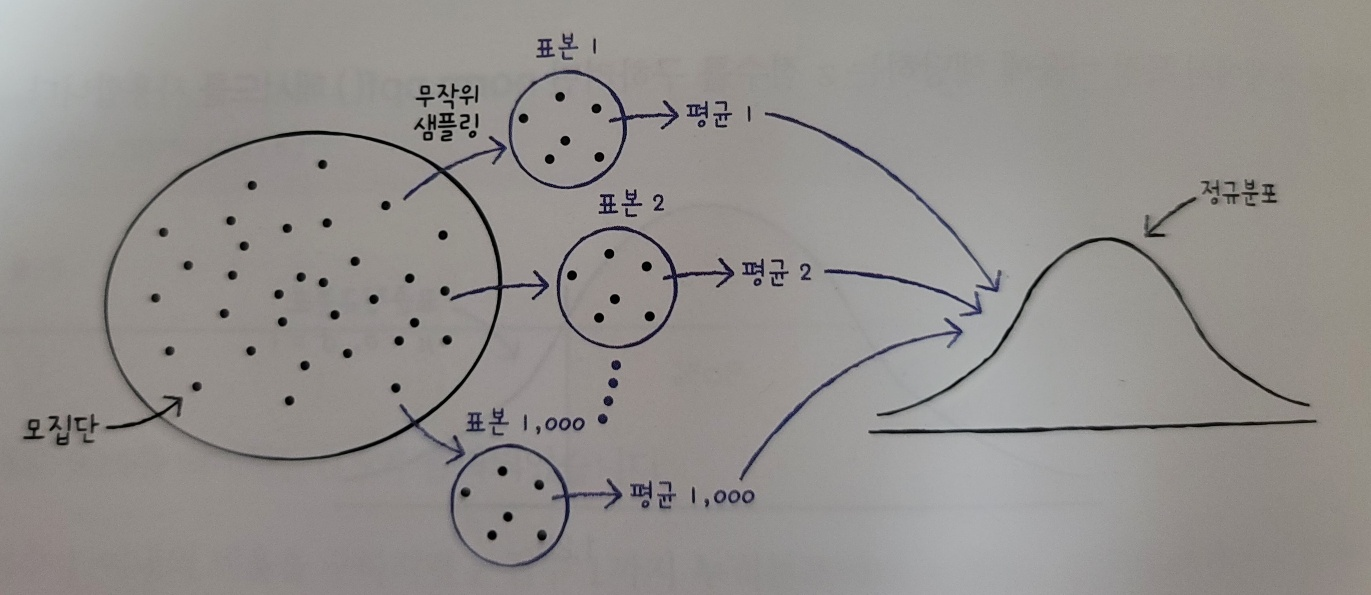
import gdown
gdown.download('https://bit.ly/3pK7iuu', 'ns_book7.csv', quiet=False)
import pandas as pd
ns_book7 = pd.read_csv('ns_book7.csv', low_memory=False)
ns_book7.head()대출건수열로 히스토그램 생성
그래프를 보면 정규분포와 상당히 거리가 멀기대문에 무작위로 샘플링한 표본의 평균을 히스토그램으로 그려봄
import matplotlib.pyplot as plt
plt.hist(ns_book7['대출건수'], bins=50)
plt.yscale('log')
plt.show()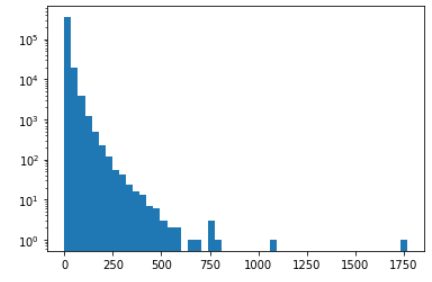
샘플링
무작위로 1000개의 표본은 샘플링, 30개씩 뽑아 표본을 만들고 평균을 계산을 반복
np.random.seed(42)
sample_means = []
for _ in range(1000):
m = ns_book7['대출건수'].sample(30).mean()
sample_means.append(m)
plt.hist(sample_means, bins=30)
plt.show()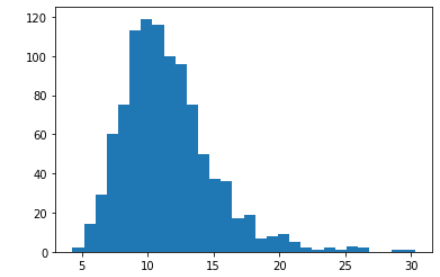
샘플링 크기와 정확도
무작위로 뽑은 표본의 통계량과 실제 모집단의 통계량과 얼마나 일치하는지 확인
# 무작위
np.mean(sample_means)
# 출력
11.539900000000001
# 실제 모집단
ns_book7['대출건수'].mean()
# 출력
11.593438968070707모집단의 평균 범위 추정하기 : 신뢰구간
표본의 파라미터(여기서는 평균)가 속할 것이라고 믿는 모집단의 파라미터 범위
주제분류번호가 00으로 시작하고 도서명에 파이썬이 포함된 행을 불리언 배열로 만들어 도서를 추출
python_books_index = ns_book7['주제분류번호'].str.startswith('00') & \
ns_book7['도서명'].str.contains('파이썬')
python_books = ns_book7[python_books_index]
python_books.head()
# 파이썬 도서의 대출건수 평균
python_mean = np.mean(python_books['대출건수'])
python_mean
# 출력
14.749003984063744중심극한정리를 적용, 모집단의 표준편차가 표본의 표준편차와 비슷하다고 가정
# 남산도서관의 파이썬 도서 대출건수로 표준편차를 구한 후 표준오차 계산
python_std = np.std(python_books['대출건수'])
python_se = python_std / np.sqrt(len(python_books))
python_se
# 출력
0.8041612072427442표본의 평균이 모집단의 평균을 중심으로 95%이내 포함된다고 확신하고 싶으면
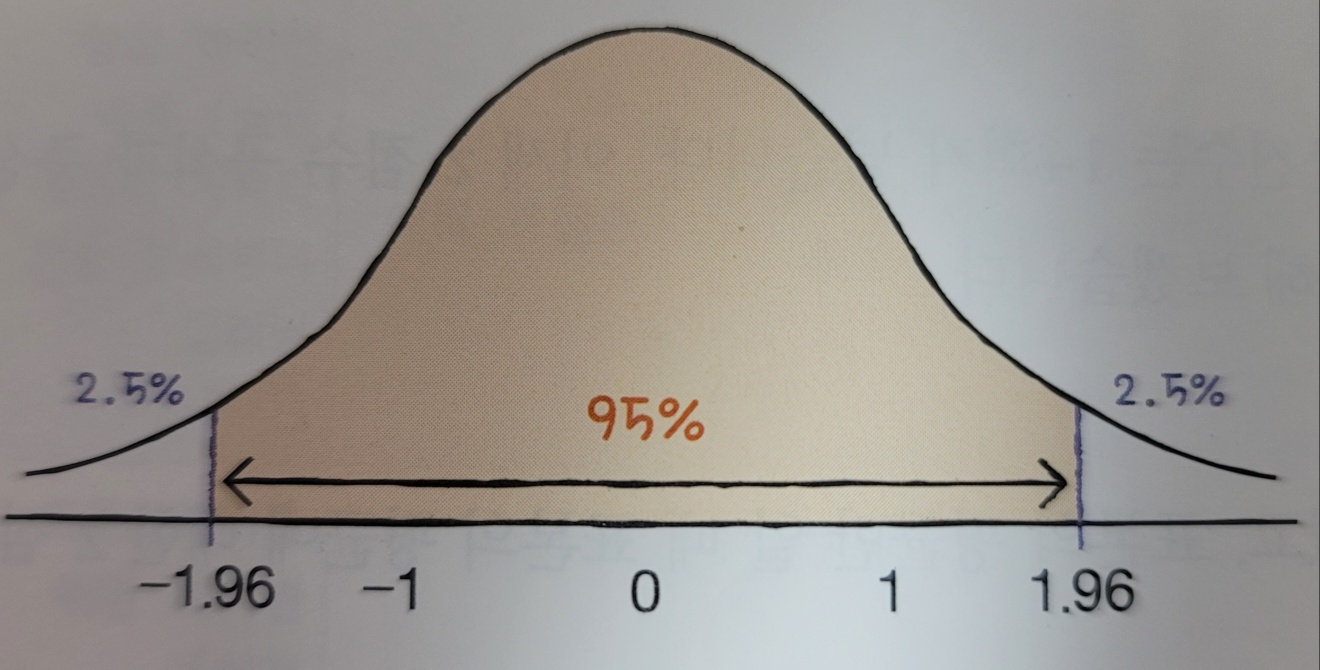
stats.norm.ppf(0.975)
# 출력
1.959963984540054
stats.norm.ppf(0.025)
#출력
-1.9599639845400545표준오차python_se와 z점수를 곱하여 파이썬 도서의 대출건수 평균인 python_mean 데이터프레임이 속할 범위구한다.
print(python_mean-1.96*python_se, python_mean+1.96*python_se)
# 출력
13.172848017867965 16.325159950259522해석
‘모집단의 평균이 13.2에서 16.3 사이에 놓여있을 거라 95%확신한다.’ 또는 ‘95% 신뢰구간에서 파이썬 도서의 모집단 평균이 13.2에서 16.3 사이에 놓여있다’
통계적 의미 확인하기 : 가설검정
표본에 대한 정보를 사용해 모집단의 파라미터에 대한 가정을 검정하는 것
표본 사이에 통계적으로 의미가 없다고 예상되는 가설 귀무가설 ,
표본 사이에 통계적인 차이가 있다는 가설 대립가설
z점수로 가설 검증하기
cplus_books_index = ns_book7['주제분류번호'].str.startswith('00') & \
ns_book7['도서명'].str.contains('C++', regex=False)
cplus_books = ns_book7[cplus_books_index]
cplus_books.head()c++의 도서권수 확인
len(cplus_books)
# 출력
89
cplus_mean = np.mean(cplus_books['대출건수'])
cplus_mean
# 출력
11.595505617977528
# 표준오차 계산
cplus_se = np.std(cplus_books['대출건수'])/np.sqrt(len(cplus_books))
cplus_se
# 출력
0.9748405650607009C++도서와 파이선 도서의 평균차이 계산
(python_mean - cplus_mean) / np.sqrt(python_se**2 + cplus_se**2)
# 출력
2.495408195140708
# 누적분포
stats.norm.cdf(2.50)
# 출력
0.9937903346742238t-검정으로 가설 검증하기 : ttest_ind() 함수
사이파이의 ttest_ind() 함수는 t-검정을 수행함, p-값은 0.03으로 0.05보다 작으며 귀무가설을 기각하며 두 도서의 대출 건수 평균의 차이는 있다.
t, pvalue = stats.ttest_ind(python_books['대출건수'], cplus_books['대출건수'])
print(t, pvalue)
# 출력
2.1390005694958574 0.03315179520224784정규분포가 아닐 때 가설 검증 : 순열검정
모집단의 분포가 정규분포를 따르지 않거나 분포를 알 수 없을때 사용하는 방법, 모집단의 파라미터를 추정하지 않기 때문에 비모수검정 방법중 하나임
- 두 표본의 평균의 차이를 계산한 후 두 표본을 섞고 무작위로 두 그룹으로 나눈다.
- 두 그룹은 원래 표본의 크기와 동일하게 만든다.
- 두 그룹에서 평균의 차이를 계산한다.
- 여러번 박복해서 평균 차이가 무작위로 나눈 그룹의 평균 차이보다 크거나 작은 경우를 헤아려 p-값을 계산한다.
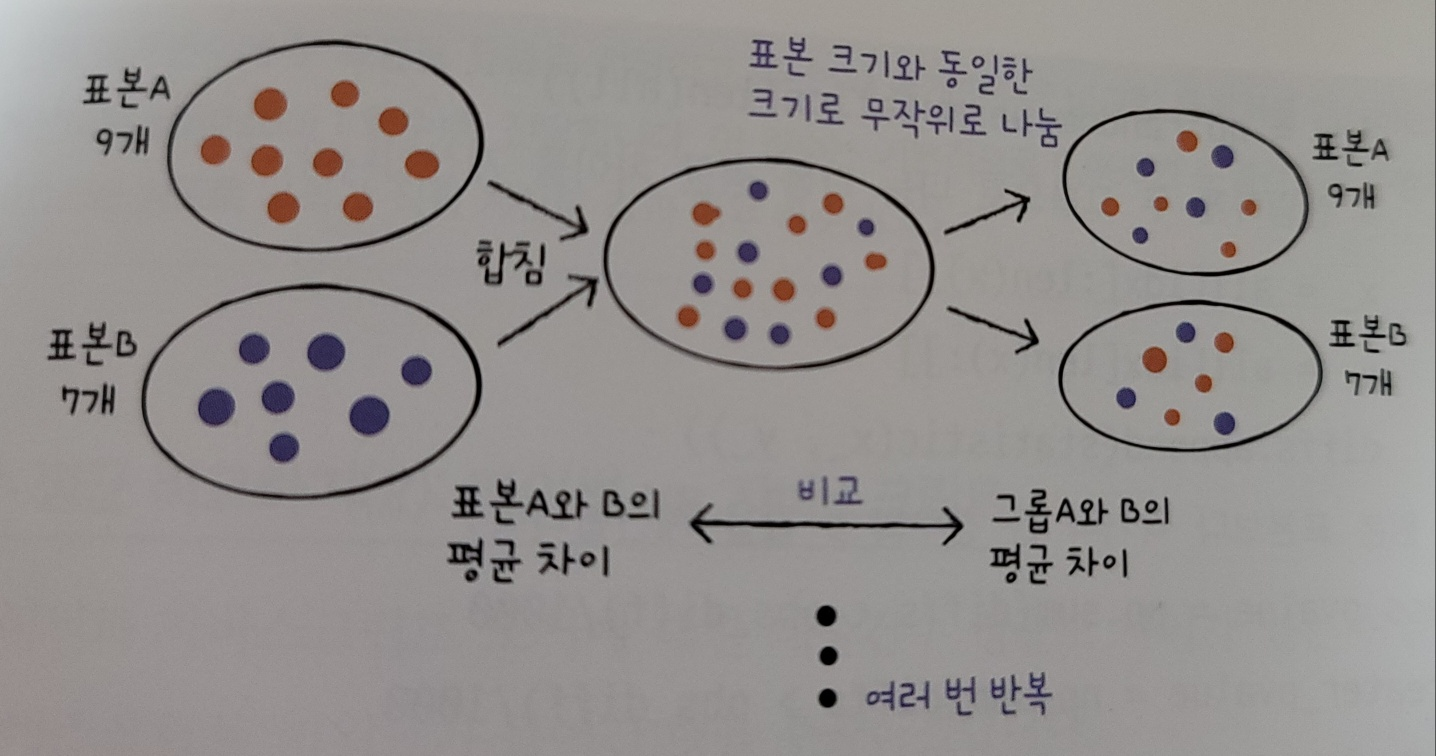
도서 대출건수 평균 비교하기(1) : 파이썬 vs C++
순열검정을 계산해 0.022라는 값을 도출함.
# 두개의 배열을 받아 평균 구하기
def statistic(x, y):
return np.mean(s) - np.mean(y)
def permutation_test(x, y):
# 표본의 평균 차이를 계산합니다.
obs_diff = statistic(x, y)
# 두 표본을 합칩니다.
all = np.append(x, y)
diffs = []
np.random.seed(42)
# 순열 검정을 1000번 반복합니다.
for _ in range(1000):
# 전체 인덱스를 섞습니다.
idx = np.random.permutation(len(all))
# 랜덤하게 두 그룹으로 나눈 다음 평균 차이를 계산합니다.
x_ = all[idx[:len(x)]]
y_ = all[idx[len(x):]]
diffs.append(statistic(x_, y_))
# 원본 표본보다 작거나 큰 경우의 p-값을 계산합니다.
less_pvalue = np.sum(diffs < obs_diff)/1000
greater_pvalue = np.sum(diffs > obs_diff)/1000
# 둘 중 작은 p-값을 선택해 2를 곱하여 최종 p-값을 반환합니다.
return obs_diff, np.minimum(less_pvalue, greater_pvalue) * 2
permutation_test(python_books['대출건수'], cplus_books['대출건수'])
# 출력
(3.1534983660862164, 0.022)도서 대출건수 평균 비교하기(2) : 파이썬 vs 자바스크립트
귀무가설이며 차이가 거의 없다.
java_books_indx = ns_book7['주제분류번호'].str.startswith('00') & \
ns_book7['도서명'].str.contains('자바스크립트')
java_books = ns_book7[java_books_indx]
java_books.head()
print(len(java_books), np.mean(java_books['대출건수']))
permutation_test(python_books['대출건수'], java_books['대출건수'])
# 출력
105 15.533333333333333
(-0.7843293492695889, 0.566)머신러닝으로 예측하기
머신러닝 패키지 : 사이킷런
모델
머신러닝으로 학습된 패턴을 저장하는 소프트웨어 객체를 의미함
지도학습, 비지도학습
지도학습은 데이터에 있는 각 샘플에 대한 정답(타깃)을 알고있는 경우,
비지도학습은 입력 데이터는 있지만 타깃이 없는 경우
모델 훈련하기
A를 훈련세트, B를 테스트 세트라고 부름
일반적으로 훈련 데이터가 테스트 데이터보다 크며, 보통 테스트 데이터는 전체 데이터의 20~25%를 사용한다.
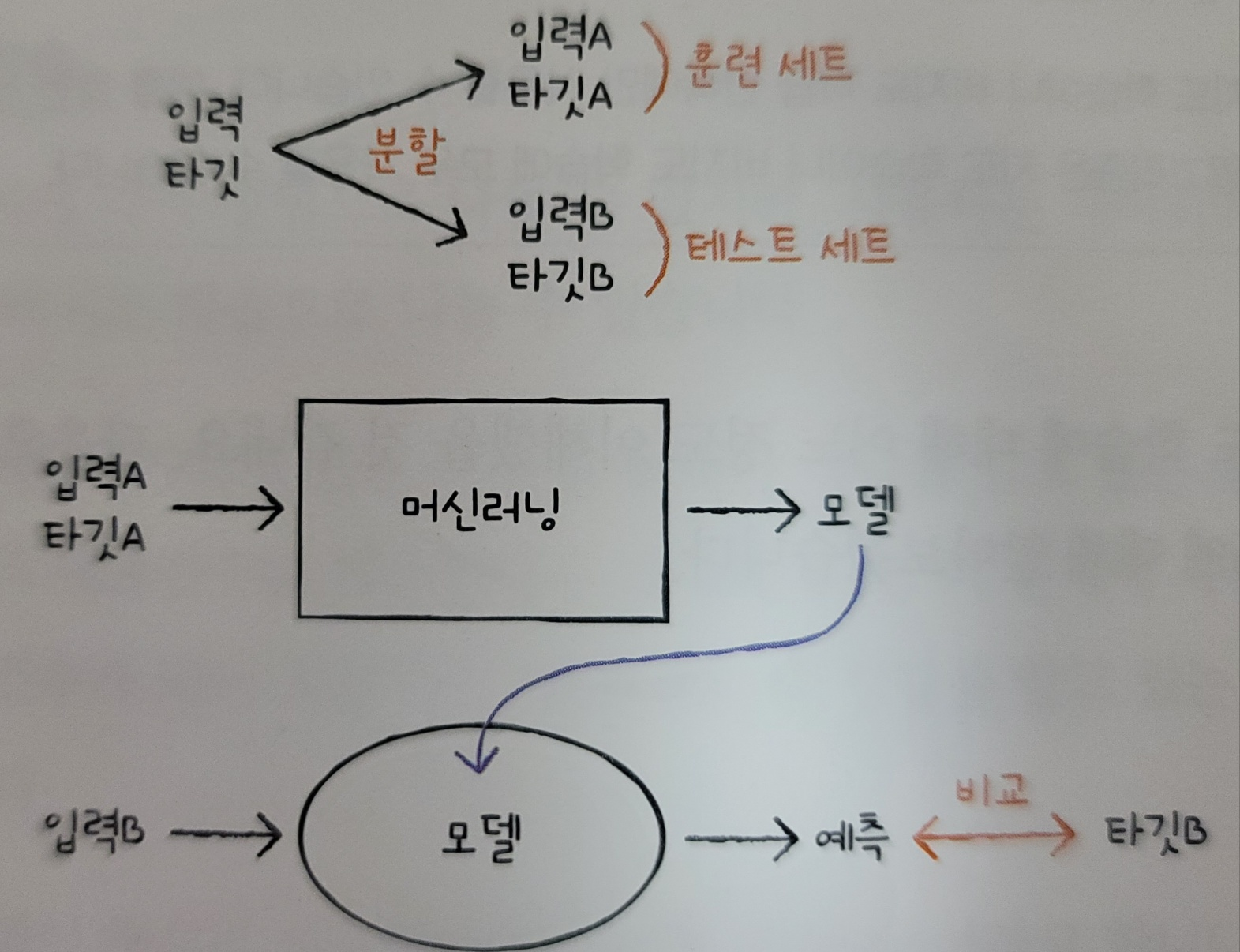
훈련 세트와 테스트 세트로 나누기 : train_test_split() 함수
특정 성향에 몰리는 것을 방지하기 위해 데이터를 무작위로 섞은 후 샘플을 훈련 세트와 테스트 세트로 나눔
import gdown
gdown.download('https://bit.ly/3pK7iuu', 'ns_book7.csv', quiet=False)
import pandas as pd
ns_book7 = pd.read_csv('ns_book7.csv', low_memory=False)
ns_book7.head()
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(ns_book7, random_state=42)
print(len(train_set), len(test_set))
# 출력
282577 94193선형 회귀 모델로 훈련
도서권수열을 사용해 대출건수를 예측, 열을 Feature라고 함
X_train = train_set[['도서권수']]
y_train = train_set['대출건수']
print(X_train.shape, y_train.shape)
# 출력 2차원, 1차원 배열
(282577, 1) (282577,)
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X_train, y_train)
훈련된 모델을 평가하기 : 결정계수 score() 메서드
0~1값을 가지므로 1에 가까울수록 관계가 깊다고 의미
X_test = test_set[['도서권수']]
y_test = test_set['대출건수']
lr.score(X_test, y_test)
# 출력
0.10025676249337112
# 대출건수로 대출건수를 예측하는 모델
lr.fit(y_train.to_frame(), y_train)
lr.score(y_test.to_frame(), y_test)
# 출력
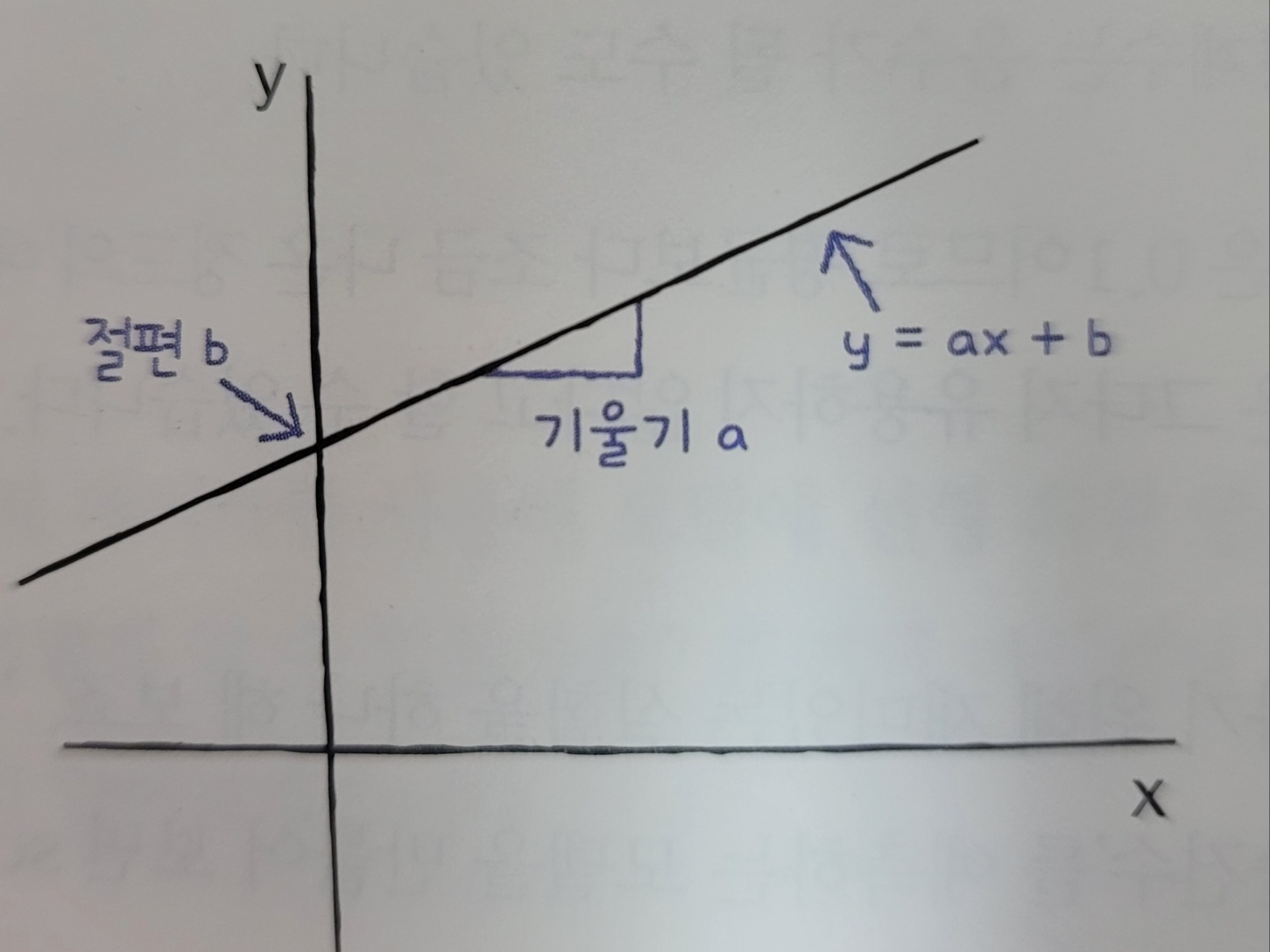
1.0연속적인 값 예측하기 : 선형 회귀
선형 함수를 이용해 모델을 만드는 알고리즘으로 입력에 기울기를 곱하고 y축과 만나는 절편을 더하여 예측을 만드는 것
카테고리 예측하기 : 로지스틱 회귀
두개의 카테고리로 구분하는 경우 이진 분류, 세 개이상의 카테고리 다중분류
타킷 카테고리를 클래스라고 부름, 0일때 음성 클래스, 1인경우 양성 클래스
선형 함수를 사용하지만 예측을 만들기 전에 로지스틱 함수를 거치는 과정을 함
로지스틱 회귀 모델 훈련하기
borrow_mean = ns_book7['대출건수'].mean()
# 대출건수 평균보다 높으면 양성 클래스
y_train_c = y_train > borrow_mean
y_test_c = y_test > borrow_mean
from sklearn.linear_model import LogisticRegression
logr = LogisticRegression()
logr.fit(X_train, y_train_c)
logr.score(X_test, y_test_c)
# 출력(정확도)
0.7106154385145393
# 양성, 음성 클래스 분포 확인
y_test_c.value_counts()
# 출력
False 65337
True 28856
Name: 대출건수, dtype: int64함수
| 메서드 | 기능 |
|---|---|
| sklearn.model_selection.train_test_split() | 입력된 데이터를 훈련/테스트 세트로 나눔 |
| sklearn.linear_model.LinearRegression | 선형 회귀를 수행 |
| LinearRegression.fit() | 모델을 훈련 |
| LinearRegression.score() | 모델의 성능을 평가 |
| LinearRegression.predict() | 샘플에 대한 예측을 만듬 |
| sklearn.linear_model.LogisticRegression | 로지스틱 회귀 수행 |
| sklearn.dummy.DummyClassifier | 입력값을 고려하는 대신 타깃에서 다수의 클래스를 예측으로 사용 |
소감…
오늘부로 혼자 공부하는 데이터분석 with 파이썬 책을 모두 끝내버렸다. 솔직히 말하자면 100% 이해하지 못했다.. 책을 끝내고 난 느낌은 아 데이터분석이 이런거다라고 찍먹 하는 정도의 지식을 얻은 느낌이다. 전문적으로 데이터분석을 하려면 더 많은 시간을 투자해서 공부를 해야겠다는 생각이 계속들었다.. 나와는 조금 안맞는거 같기도..
다음책은 기초를 다시 다지기 위해서 자바스크립트/타입스크립트 혹은 요즘 공부하는 플러터 책을 구입해서 진행해보아야겠다.
자랑
혼공학습단 9기 완주를 하고 최우수혼공족 5인에 들었다!

