🍋Linear+SGD Model - Regression

Overview

When Do You Need Regression?

Typically, you need regression to answer whether and how some phenomenon influences the other or how several variables are related. For example, you can use it to determine if and to what extent experience or gender impacts salaries.

What Is Regression?

Regression searches for relationships among variables. For example, you can observe several employees of some company and try to understand how their salaries depend on their features, such as experience, education level, role, city of employment, and so on.

một căn nhà rộng x1 m2�1 m2, có x2�2 phòng ngủ và cách trung tâm thành phố x3 km�3 km có giá là bao nhiêu. Giả sử chúng ta đã có số liệu thống kê từ 1000 căn nhà trong thành phố đó, liệu rằng khi có một căn nhà mới với các thông số về diện tích, số phòng ngủ và khoảng cách tới trung tâm, chúng ta có thể dự đoán được giá của căn nhà đó không? Nếu có thì hàm dự đoán y=f(x)�=�(�) sẽ có dạng như thế nào. Ở đây x=[x1,x2,x3]�=[�1,�2,�3] là một vector hàng chứa thông tin input, y� là một số vô hướng (scalar) biểu diễn output (tức giá của căn nhà trong ví dụ này).

Lưu ý về ký hiệu toán học: trong các bài viết của tôi, các số vô hướng được biểu diễn bởi các chữ cái viết ở dạng không in đậm, có thể viết hoa, ví dụ x1,N,y,k�1,�,�,�. Các vector được biểu diễn bằng các chữ cái thường in đậm, ví dụ y,x1�,�1. Các ma trận được biểu diễn bởi các chữ viết hoa in đậm, ví dụ X,Y,W�,�,�.

Một cách đơn giản nhất, chúng ta có thể thấy rằng: i) diện tích nhà càng lớn thì giá nhà càng cao; ii) số lượng phòng ngủ càng lớn thì giá nhà càng cao; iii) càng xa trung tâm thì giá nhà càng giảm. Một hàm số đơn giản nhất có thể mô tả mối quan hệ giữa giá nhà và 3 đại lượng đầu vào là:

y≈f(x)=^y�≈�(�)=�^f(x)=w1x1+w2x2+w3x3+w0    (1)�(�)=�1�1+�2�2+�3�3+�0    (1)trong đó, w1,w2,w3,w0�1,�2,�3,�0 là các hằng số, w0�0 còn được gọi là bias. Mối quan hệ y≈f(x)�≈�(�) bên trên là một mối quan hệ tuyến tính (linear). Bài toán chúng ta đang làm là một bài toán thuộc loại regression. Bài toán đi tìm các hệ số tối ưu {w1,w2,w3,w0}{�1,�2,�3,�0} chính vì vậy được gọi là bài toán Linear Regression.

• 가지고 있는 데이터를 잘 표현할 수 있는 선형함수 찾기
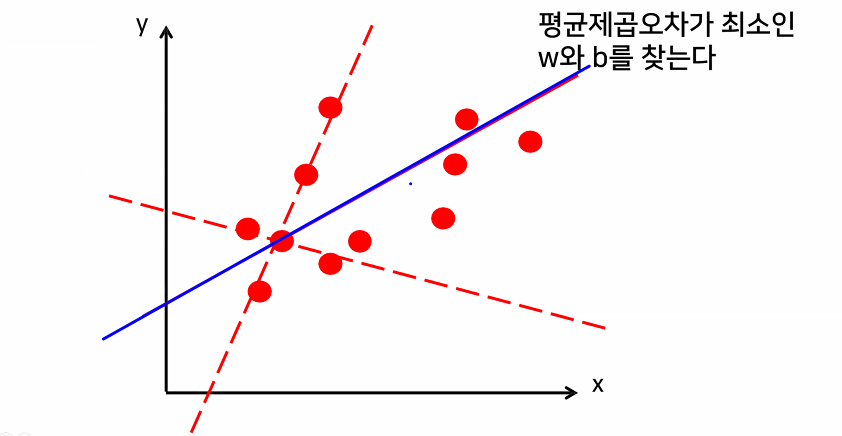
• 모든 데이터를 설명할 수 있는 직선은 없다
• 데이터를 퇴대한 잘 설명하는 선형함수 찾기
• • 오차(실제값과 예측값의 차이들의 합)가 최소가 되느 직선 찾기>가장 좋은 선형 함수>예측 함수로 사용
• 성형함수의 갯수가 무한대이다
• 무한개의 선형함수를 계산하지말고 계산할 선형함수의 갯수를 줄여보자(2가지 방법이 존재)

무한개의 선형함수를 계산하지 말고 계산할 선형함수의 갯수를 줄여보자

1. 수학 공식을 이용한 해석적 방법

• 한번에 계산할 공식이 존재
• 단점: 공식이 완벽하지 않다 > 값이 잘 못됐을때 고칠 수 없음
• 장점: 매우 빠르다
• 모델: Linear Regression, Lasso, Ridge

1. 경사하강법

• 점진적으로 정답을 찾아간다
• 단점: 속도가 느리다
• 장점: 값이 잘 못됐을때 고칠 수 있음
• 모델: SGDRegressor

! 결론:

1. 가지고 있는 데이터를 최대한 잘 설명할 직선 찾기
2. 오차를 계산해서 오차가 가장 작은 직선 찾기
3. 무한개의 직선을 계산하지 않고 특성 갯수의 직선만 계산

actual value - predict value : error

**성적 데이터 생성**

import pandas as pd

data = pd.DataFrame(
    [
    [2,20],[4,40],[8,80],[9,90]
], columns = ['시간','성적']
)
data

**문제와 정답 나누기**

x = data[['시간']] #2차원(문제데이터)
y= data['성적']#1차원(정답데이터)

1. 수학 공식을 이용한 해석적 모델

Linear Regression

• LinearRegression
• 한번에 정답 찾기
• 공식이 완벽하지 않아서 오답을 출력할때도 있다
• 오답이 여도 수정 불가
• 하지만 빠르다

from sklearn.linear_model import LinearRegression

lr = LinearRegression()

lr.fit(x,y)

# 최적의 선형함수 y= 10x+0 
# y = wx + b
# w: 가중치(기울기)
# b: 절편 (편향)

# 가중치
lr.coef_

# 절편
lr.intercept_

2. 경사하강법

Gradient Descent Algorithm

• sgdRegressor
• 점진적으로 직선을 찾아가는 방법
• 여러번걸쳐서 찾아가기 때문에 잘못되어도 다시 찾을 수 있다
• 여러번에 걸쳐서 찾아가기 때무네 느리다

linear regression la di thang len

SGD regressor la di xuong doc

from sklearn.linear_model import SGDRegressor

sgd = SGDRegressor(eta0=0.00001)

sgd.fit(x,y)

sgd.coef_

sgd.intercept_

# y = 9.85608274x + 1.04236436
sgd.predict([[5]])

Add more (x )data

data1 = pd.DataFrame(
    [
    [2,10,20],[4,20,41],[8,40,81],[9,45,91]
], columns = ['시간','지난성적','성적']
)
data1

# indexing 사용할 수 있는 요소 = 인덱스 번호 컬럼 이름 리스트
# fancy인덱싱 = 다양한 방법을 사용하는 인덱싱
x = data1[['시간','지난성적']] #2차원(문제데이터)

y= data1['성적']#1차원(정답데이터)

# 수학 공식을 이용한 해석적 모델
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(x,y)
lr.coef_
lr.intercept_
lr.predict([[7,35]])

# 경사하강법
from sklearn.linear_model import SGDRegressor
SGDRegressor(eta0 = 0.0001)
sgd.fit(x,y)
sgd.coef_
sgd.intercept_
sgd.predict([[5,25]])