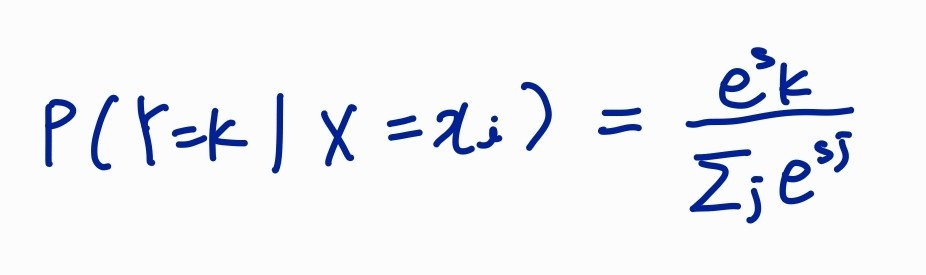지난 시간 Review
Linear Classifier는 이미지를 입력받으면 하나의 긴 벡터로 편다.
예시)
input image는 32x32x3 픽셀이고 이를 긴 열벡터로 펼친다.
32x32는 이미지의 높이와 너비이며 3은 RGB 채널이다.
그리고 파라미터 행렬 W가 있는데 이 행렬은 이미지 픽셀과 연산하여 CIFAR-10의 각 10개의 클래스에 해당하는 클래스 스코어를 계산해낸다.
고양이 클래스의 스코어가 더 크다는 것은 분류기가 이 이미지가 고양이일 것 같다고 예측하는 것이다.
Linear classification을 각 클래스 템플릿으로 보면 행렬 W에는 각 10개의 클래스와 이미지의 모든 픽셀에 대응되는 요소들이 있다.
이것은 "이 픽셀이 클래스를 결정하는데 얼마나 중요한 역할을 하는지"를 의미한다. -->가중치를 의미
행렬 W의 각 행들이 해당하는 그 클래스의 템플릿이 되는 것이다.
행렬 W의 각 행은 "이미지의 픽셀 값"과 "해당 클래스" 사이의 가중치가 되기 때문에 각 행을 풀어서 다시 한 이미지로 재구성하면 각 클래스에 대응하는 학습된 템플릿을 볼 수 있다.
Linear classification이 고차원 공간에서의 일종의 "결정 경계"를 학습한다는 측면으로 볼 수 있는데, 그 공간의 차원은 이미지의 픽셀 값에 해당하게 된다.
오늘 진도
어떻게 행렬 W를 만드는가?
가장 좋은 행렬 W를 구하는데 어떻게 training data를 활용해야하는가?
만들어진 행렬 W가 좋은지 나쁜지를 정량화 할 방법이 필요하다!
--> 이때 사용되는 것이 Loss function이다.
Image Classification에서 쓸만한 몇 가지 손실함수를 알아보자!
행렬 W가 될 수 있는 모든 경우의 수에 대해서 가장 덜 구린 W가 무엇인지 찾고 싶다.--> Optimization
어떤 알고리즘이든 일단 어떤 X와 y가 존재하고, 우리가 만들 파라미터 W에 W가 얼마나 좋은지를 정량화하는 Loss function을 만든다.
결국 training data의 loss를 최소화하는 어떤 W를 찾게 된다.
ex) Multi-class SVM(SUpport Vector Machine) Loss
여러 클래스를 다루기 위한 SVM
Training Data(X, y)
X는 알고리즘의 입력
y는 예측하고자 하는 것(Label, Target) = 정답 category

Loss Function의 Logic
-
Loss Function i를 구하기 위해 우선 True인 카테고리를 제외한 나머지 카테고리 Y의 합을 구한다.
=맞지 않는 카테고리를 전부 합치는 것 -
True 카테고리의 score와 False 카테고리의 score를 비교한다.
만악 True 카테고리의 점수가 False 카테고리의 점수보다 높고, 그 격차가 일정 마진 이상이라면 True인 스코어가 다른 False 카테고리보다 훨씬 더 크다는 것을 의미한다. 그러면 Loss는 0이 된다. -
False 카테고리의 모든 값을 합치면 그게 한 이미지의 최종 Loss가 되는 것이다. 그리고 전체 training dataset에서 그 Loss들의 평균을 구한다.
이를 수식화하면
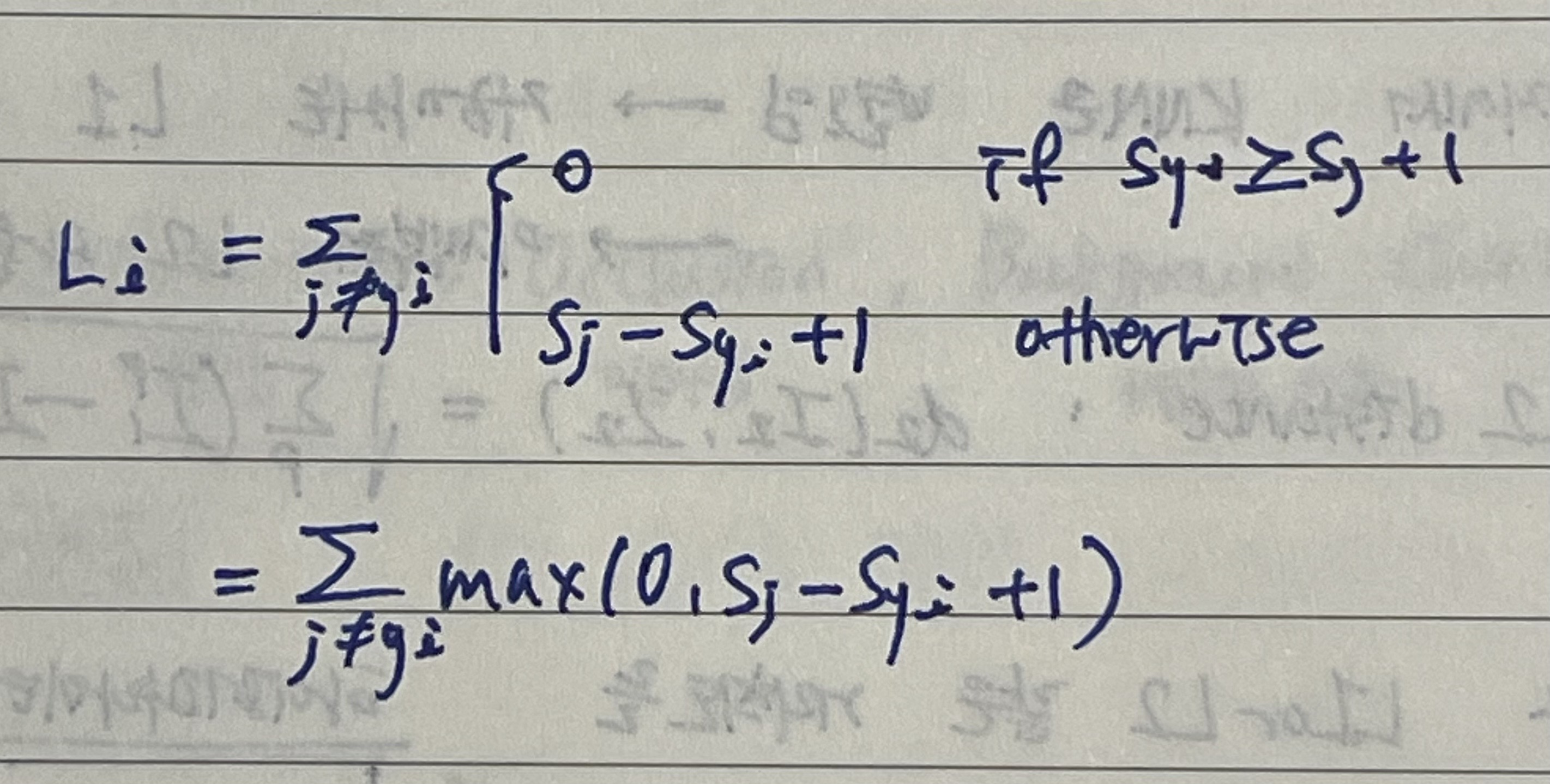
-
0과 다른 값의 최댓값, Max(0, value)와 같은 식으로 Loss Function을 만드는데, 이런 류의 Loss Function을 hinge loss(경첩)라고 부르기도 한다.
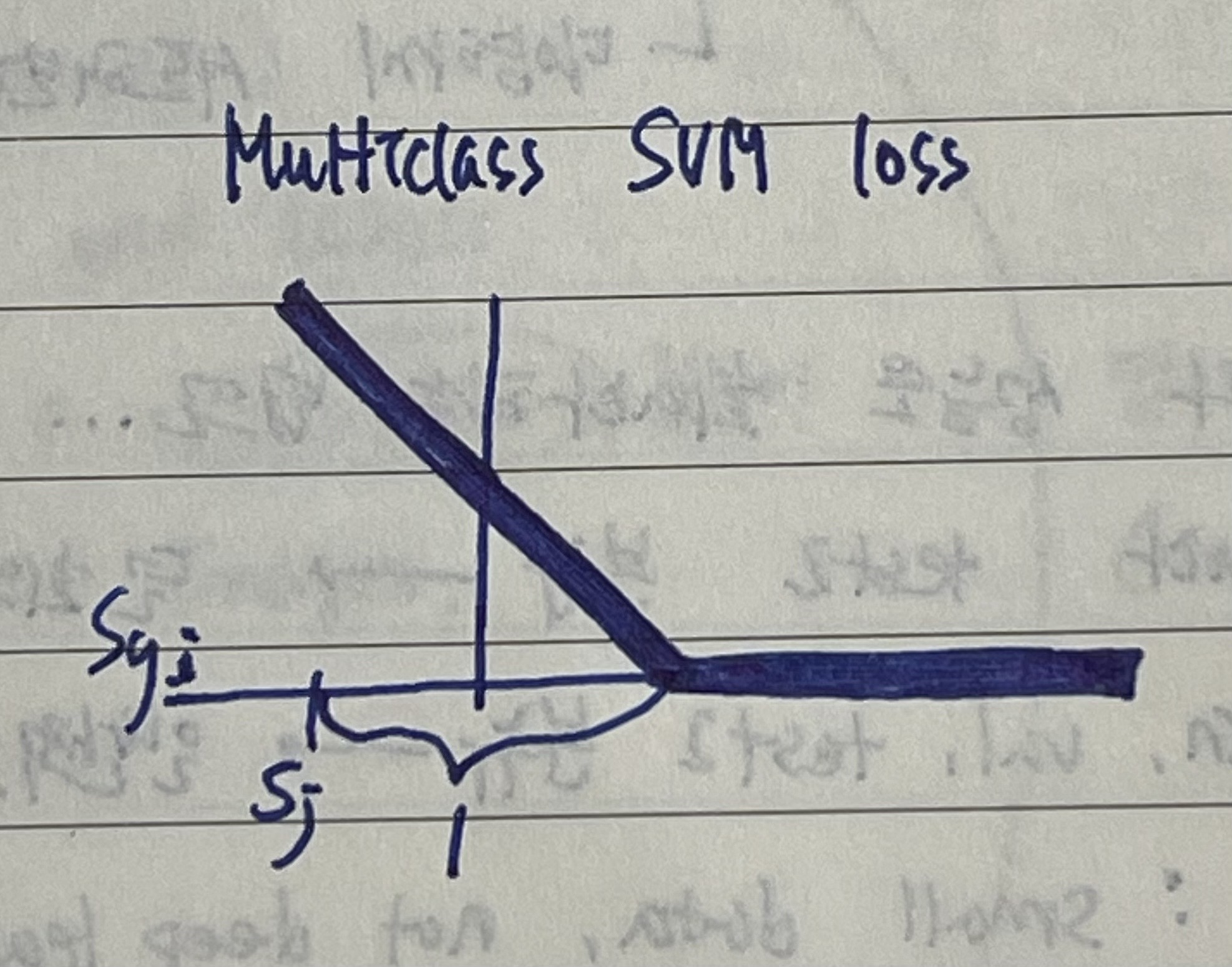
x축은 Syi, y축은 Loss이다.
정답 category의 점수가 올라갈수록 Loss가 선형적으로 줄어드는 것을 알 수 있다.
이 Loss는 0이 된 이후에도 Safty margin을 넘어설 때까지 더 줄어든다.
Loss가 0이 됐다는 건 클래스를 잘 분류했다는 뜻이다.
S는 분류기의 출력으로 나온 예측된 스코어이다.
Yi는 이미지의 실제 정답 카테고리이다.(int값)
따라서 Syi는 training set의 i번째 이미지의 정답 클래스의 스코어이다.
Loss가 말하고자 하는 것은 정답 스코어가 다른 스코어들보다 높으면 좋다는 것이다.
아래는 cat, car, frog에 대한 각각의 loss와 최종 loss를 구하는 과정이다.


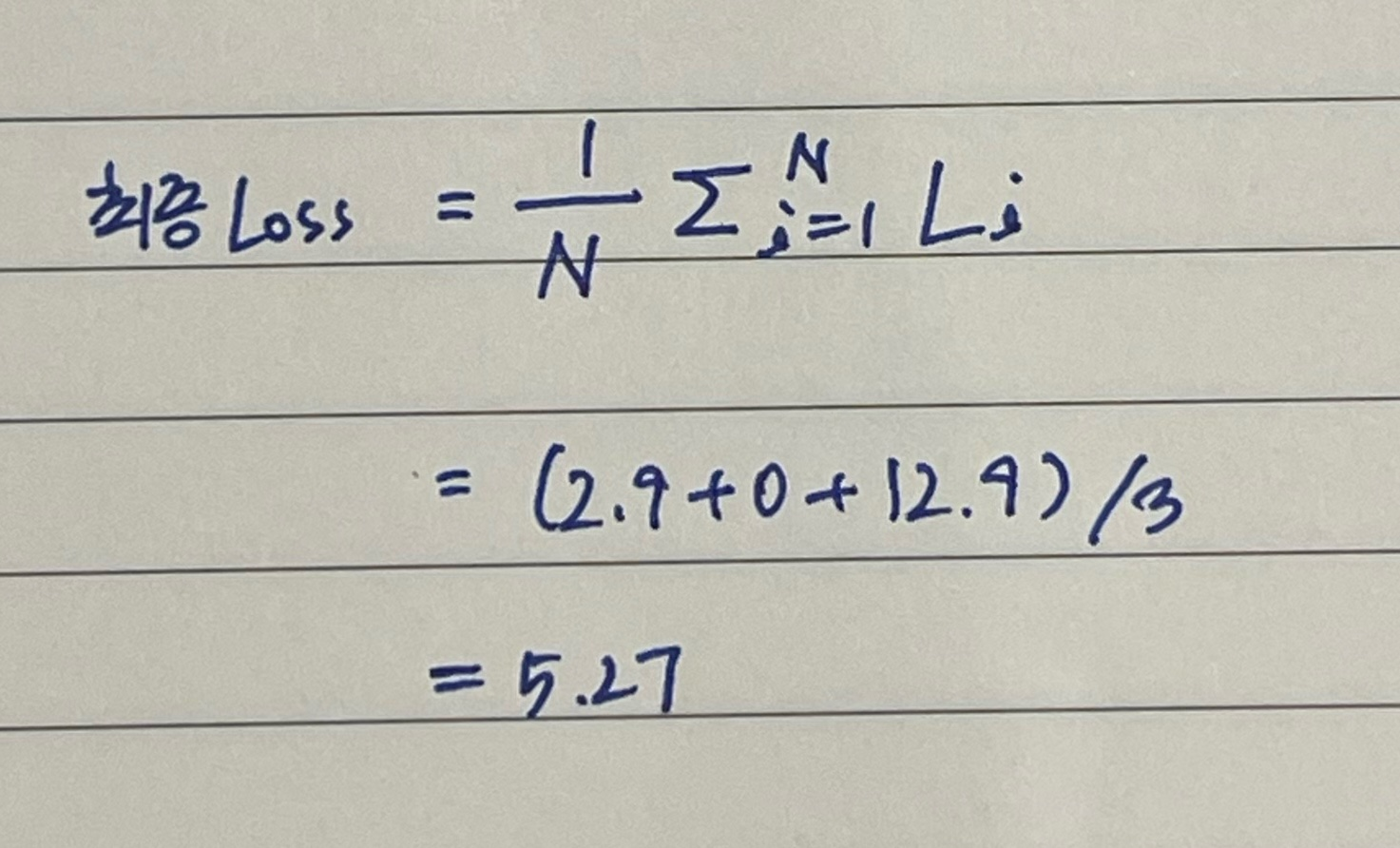
이것이 의미하는 바는 우리의 분류기가 5.3점 만큼 이 training set을 구리게 분류하고 있다는 "정량적 지표"라는 것이다.
우리는 사실 Loss Function에서의 score를 신경쓰지 않고 여러 스코어 간의 상대적인 차이를 궁금해 한다.
정답 스코어가 다른 스코어에 비해 얼마나 큰지만을 궁금해한다.
행렬 W를 전체적으로 스케일링한다고 생각해보면 결과 스코어도 바뀔 것이다.
Q) 차의 loss를 바꾼다면 어떤 일이 일어날까?
A) score가 이미 크기 때문에 결과가 바뀌지 않는다.
Q) SVM loss의 최대/최소 값은 무엇일까?
A) 최소는 0, hinge loss를 생각해보면 최대는 무한대이다.
Q) 만약 모든 스코어가 거의 0에 가깝고 값이 서로 비슷하다면 Loss는 어떻게 될까?
A) class 수 - 1
왜냐하면 Loss를 계산할 때 정답이 아닌 클래스를 순회하는데 그러면 class 수 - 1를 순회한다. 비교하는 두 스코어가 비슷하니까 margin 1만 남고 1 * (class 수 - 1) 여서 class 수 - 1이 된다.
Q) SVM Loss는 정답인 클래스는 빼고 다 더했었다. 정답인 것도 같이 더하면 어떻게 될까?
A) Loss에 1이 증가한다.
Q) Loss에서 전체 합을 쓰는게 아니라 평균을 쓰게 되면 어떻게 될까?
A) 영향을 미치지 않는다. 그저 loss function을 스케일링하는 것과 같다.
Q) Loss function을 제곱항으로 바꾼다면?
A) 결과는 달라질 것이다. 선형적인 결과를 비선형적인 방식으로 바꾸어주는 것이다. 그럼 loss function을 변화시키는 것이다.
아래 코드는 SVM loss form 수식을 코드화 한 것이다.
def L_i_vectorized(x, y, W):
scores = W.dot(x)
margins = np.maximum(0, scores - scores[y] + 1)
margins[y] = 0 #정답 클래스만 0으로 만들어줌
loss_i = np.sum(margins)
return loss_iQ) loss가 0이 되게 하는 W가 유일하게 하나만 존재할까?
A) 아님. 다른 W도 존재한다.
다양한 W 중 loss가 0인것을 선택하는 것은 모순이다.
=training data에 딱맞는 W를 찾는 것이다.
이러면 안되는게 우리는 test data에서의 성능에 관심있기 때문이다.
아래 모델은 다양한 W 중 loss가 0인 것을 선택했고 test data에 적응하지 못하고 있다.
Occam's Razor
다양한 가설을 가지고 있고 그 가설들 모두가 어떤 현상에 대해 설명 가능하다면, 그럼 일반적으로 더 단순한 것을 선호해야 한다.
일반적인(단순한) 것이 미래에 일어날 현상을 잘 설명할 가능성이 높기 때문이다.
-->Regularization penalty를 고안해냄
위의 식은 전체 Loss가 data loss와 Regularization loss로 구성됨을 나타내고 하이퍼파라미터인 람다도 생겼음을 보여준다.
Regularization의 종류

L2 Regularization은 가중치 행렬 W의 euclidean norm에 패널티를 준다. (모든 x의 요소가 골고루 영향을 미치기 원할 때 ex) [2.5, 2.5, 2.5, 2.5])
L1 Regularization은 행렬 W가 희소행렬이 되도록 한다.
(가중치 W에 0의 개수에 따라 모델의 복잡도를 따름 ex) [1, 0, 0, 0])
Regularization은 모델이 training set에 완벽히 fit 하지 못하도록 모델의 복잡도에 패널티를 부여하는 방법이다.
multi-class SVM 말고 Multinomial logistic regression과 softmax가 있다.
Softmax Classifier를 더 많이 쓴다.
multi-class SVM에서는 스코어 자체를 신경쓰지 않았다.
정답 클래스가 정답이 아닌 클래스들 보다 더 높은 스코어를 내면 상관 없었다.
하지만 Softmax Classifier는 스코어 자체에 의미를 부여한다.
바로 이 수식을 이용하여 스코어를 가지고 클래스 별 확률 분포를 계산하게 된다.
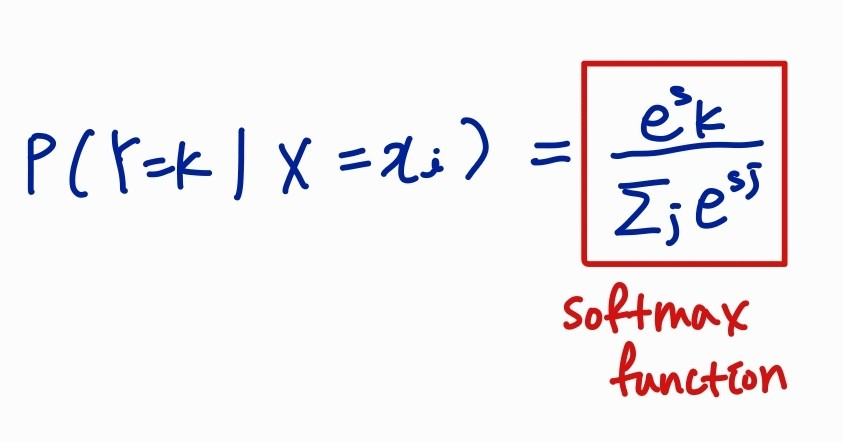
softmax 함수를 거치게 되면 우리는 결국 확률 분포를 얻을 수 있고 그게 바로 해당 클래스일 확률이 된다.
0~1 사이의 값이고 모두 더하면 1이 된다.
우리가 하는 일은 softmax에서 나온 확률이 정답 클래스에 해당하는 클래스의 확률을 1로 만드는 일이다.
loss function은 얼마나 좋은지가 아니라 얼마나 구린지를 측정하는 것이기 때문에 log에 마이너스를 취한다.
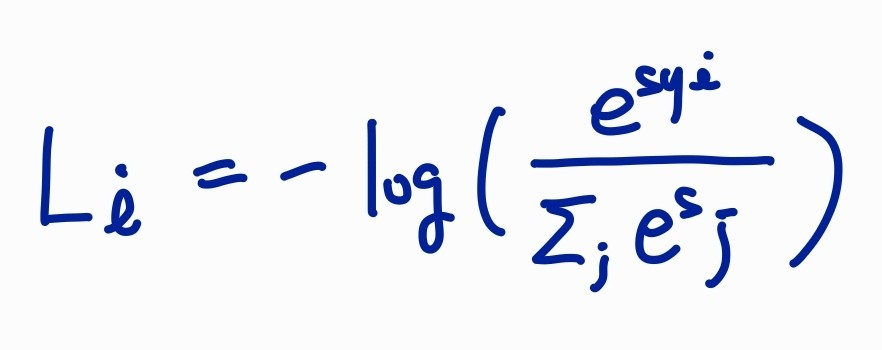
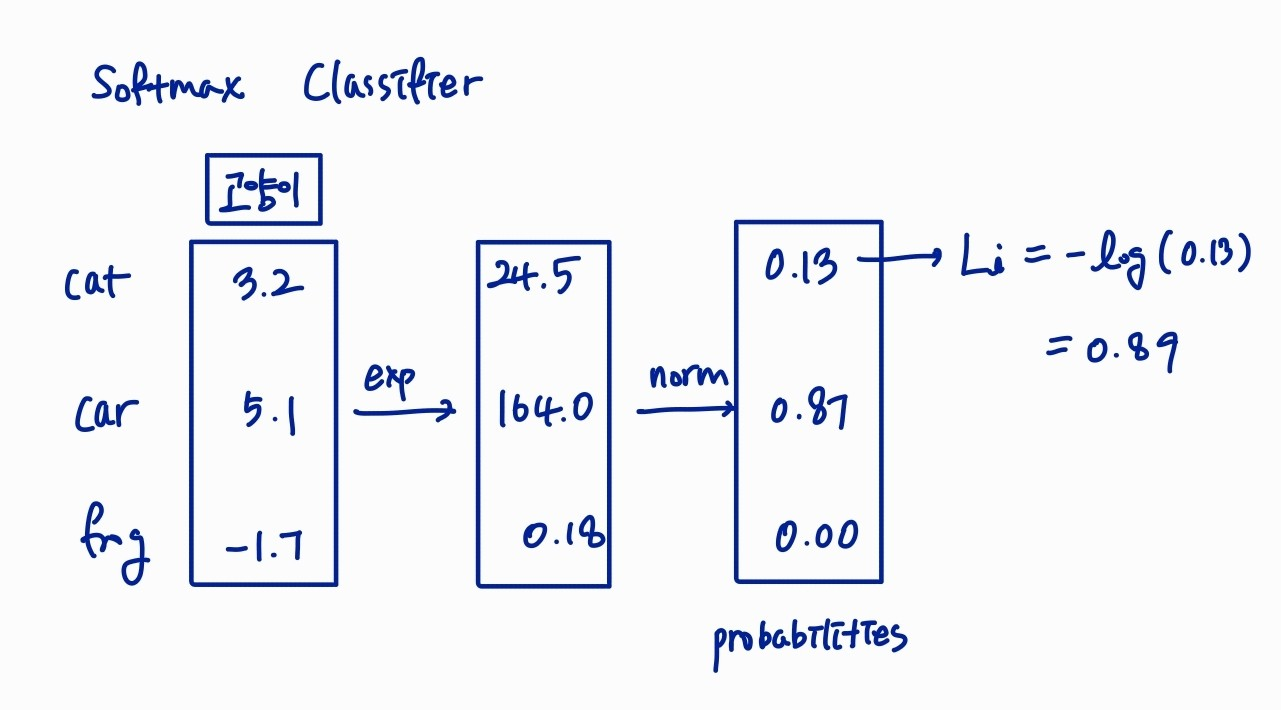
softmax는 다항 로지스틱 회귀(multinomial logistic regression)라고도 한다.
Q) softmax loss 스코어의 최댓값과 최솟값은 얼마일까?
A) Loss의 최솟값은 0이고 최댓값은 무한대이다.
Q) S가 모두 0 근처에 모여있는 작은 수일때 loss는?
A) log(C)
SVM와 softmax는 얼마나 구린지 측정하는 방법이 다르다.
SVM에서는 정답 스코어와 정답이 아닌 스코어 간의 마진을 신경썼다면
softmax에서는 확률을 구해서 -log(정답클래스)에 신경을 쓴다.
큰 성능 차이는 나지 않지만 차이가 있음을 알고 있어야한다.
Recap)
우선 입력 x로부터 스코어를 얻기 위해 Linear classifier를 사용한다.
softmax, svm loss와 같은 손실함수를 이용해서 모델의 예측값이 정답 값에 비해 얼마나 구린지 측정한다.
그리고 모델의 복잡함과 단순함을 통제하기 위해 loss function에 regularization term을 추가한다.
-->Supervised learning의 전반적인 개요이다.
딥러닝은 어떤 엄청 복잡한 함수 f를 세우고 파라미터 값이 주어졌을 때 알고리즘이 얼마나 구리게 동작하고 있는지 측정할 loss function을 작성하고 모델이 복잡해지는 것을 막기 위해 regularization term을 추가하는 것으로 구성된다. 그걸 모두 합쳐서 최종 손실 함수가 최소가 되게 하는 가중치 행렬(파라미터 행렬 W)를 구하는 것이다.
그럼 실제로 어떻게 해야할까? 어떻게 실제 loss를 줄이는 W를 찾을 수 있는 걸까?
-->최적화 Optimization 진행
NN을 사용하면 예측함수, 손실함수, regulization이 크고 복잡해져서 최적의 솔루션(minima)를 찾기 힘들 것이다.
그래서 iteration을 사용
가장 단순한 방법은 random search 이다.
임의로 샘플링한 W를 엄청 많이 모아놓고 loss를 계산해서 어떤 W가 좋을지 살펴본다.--> 개구림 쓰지 마셈
다른 방법은 local geometry이다.
쉬워보이지만 잘 작동하는 알고리즘
NN이나 linear classifier를 훈련시키는 방법
1차원 공간에서 경사는 기울기이다.
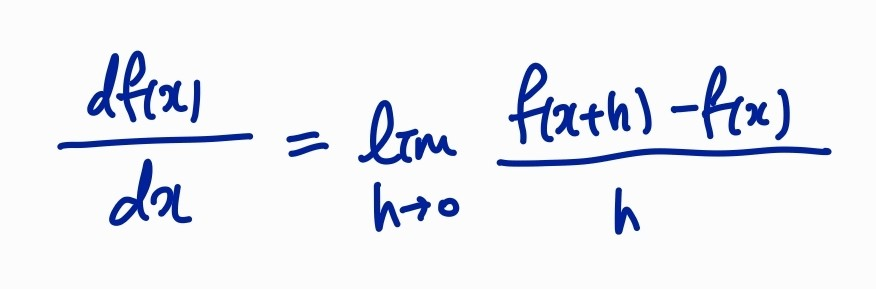
위의 사진은 기울기를 구하는 식(미분방정식)
x는 스칼라가 아니라 벡터라서 다변량이다.
gradient의 반대 방향이라면 가장 많이 내려가는 방향이다.
그래서 가장 아래인(loss가 가장 작은) 곳을 향해 간다.
--> 너무 느리다는 단점이 있음 파라미터가 많아지고 모델이 커지면 사용하지 못한다.
numerical gradient는 쉽지만 느리다.
analytical gradient는 정확하고 빠르다.
while True:
weights_grad = evaluate_gradient(loss_fun, data, weights)
weights += -step_size * weights_gradstep_size는 learning rate라고도 하고 중요한 파라미터이다.
위의 코드는 점점 minima로 가까워지는 코드이다.
여러가지 update rule들이 있다.
momentum과 Adam 등이 있다.
기본적인 알고리즘은 바로 매 스텝 아래로 내려가는 것이다.
Stochastic Gradient Descent(SGD)
N이 점점 커지면 연산량이 급속히 커진다.
그래서 minibatch로 나누어서 사용한다.
while True:
data_batch = sample_training_data(data, 256) #mini batch
weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
weights += -step_size * weights_gradLoss의 추정치와 Gradient의 추정치를 사용한다.
SGD는 DNN 알고리즘에 사용되는 기본적인 학습 알고리즘이다.
영상을 그대로 input으로 쓰지 않고이미지가 있으면 여러가지 특징 표현을 한다.
그것들을 concat하여 특징 벡터를 만들고 input 값으로 쓴다.
문제를 풀 때 어떤 특징 변환이 필요한지 알아야한다.(차원 바꾸기)
특징 변환의 한 예로 컬러 히스토그램이 있다.
이미지 전체적으로 어떤 색이 있는지 나타낸다.
Histogram of oriented gradients(HOG)도 있다.
Local orientation edges를 측정한다.
--> 이미지를 8x8 픽셀로 나누고 그 내에서 가장 지배적인 edge의 방향을 계산하고 edge directions를 양자화해서 양동이에 넣는다.
이미지에서 어떤 edge가 있는지를 특징으로 표현한다.
Bag of Words도 있다. NLP에서 영감을 받았다.
어떤 문장이 있고 BOW에서 이 문장을 표현하는 방법은 문장의 여러 단어의 발생 빈도를 특징 벡터로 사용하는 것이다.
이미지를 바로 사용하기 어려워서 시각 단어로 나타낸다.
이미지들을 조각 내고 K-means와 같은 알고리즘으로 군집화한다.
시각 단어는 다양한 색을 인식한다.
시각 단어들의 발생 빈도를 통해서 이미지를 인코딩 하는 것이다.
이미지 input의 특징 표현을 계산하고 concat해 추출된 특징들을 Linear Classifier에 넣는다.
트레이닝 중에는 extract feature는 변하지 않고 Linear Classifier만 훈련된다.
+가중치 전체를 한꺼번에 학습한다.
다음 시간
CNN, 역전파를 배울 것입니다~