2장. 수: 가상 세계를 구성하는 가장 작은 단위
2.1 수와 집합
게임을 구성하는 가상 세계를 이해하기 위한 첫걸음은 집합(set) 이라는 개념으로 수를 이해하는것이다.
어릴때 배운 집합은 서로 구분되는 원소(Element)로 구성된 묶음을 의미한다. 이러한 집합론을 소박한 집합론(Naive set theory)이라고 한다.
자연수 : 물건을 세거나 순서를 지정하기 위해 사용하는 수의 집합 (N)
정수 : 자연수와 자연수의 음수 0을 포함하는 수의 집합(Z)
유리수 : 분모가 0이 아닌 두 정수의 비율 혹은 분수로 나타낼 수 있는 수의 집합
무리수 : 두 정수 비 혹은 분수로 나타낼 수 없는 수의 집합(I)
실수 : 유리수와 무리수를 포함하는 수의 집합(R)
복소수 : 실수와 제곱하면 -1이 되는 허수 단위i를 조합해 a + bi(a,b는 실수)형태로 표현하는 수의 집합(C)
사원수 : 실수와 제곱하면 -1이 되는 세 허수 단위 i,j,k를 조합해 a+bi+cj+dk(a,b,c,d는 실수) 형태로 표현하는 수의 집합
명제중에서 증명할 필요가 없는 기본 명제를 공리(Axiom)이라고 한다.
공리를 기반으로 대상을 구분하는 집합론을 공리적 집합론(Axiomatic set theory)이라고 한다.
2.1.1 연산과 수의 구조
연산으로는 덧셈, 뺄셈, 곱셈, 나눗셈의 사칙연산이 있으며, 이들은 두개의 원소를 사용해 새로운 원소를 만들어내기 때문에 이항연산(Binary operation)이라고도 한다.
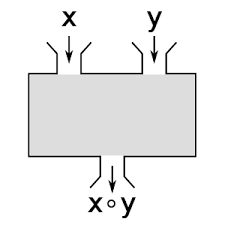
같은 집합에 속한 두 수를 투입한 이항연산의 결과가 항상 투입한 집합에 속한다면 그 이항연산은 해당 집합에 대해 닫혀 있다(Closure) 고 한다. 교환법칙(Commutaive law),결합법칙(Associative law), 분배법칙(Distributive law) 이라는 3가지 성질을 지닌다.
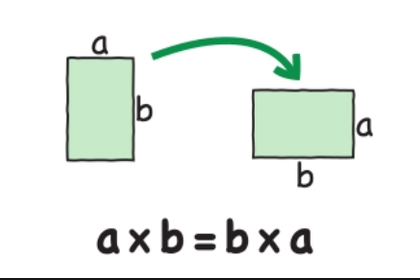
교환법칙 : 임의의 두 수를 a와 b를 연산할 때 순서에 관계없이 항상 동일한 결과가 나타나는것
결합법칙 : 연산이 두번 이상연속될때, 앞의 연산을 먼저 계산한 결과와 뒤의 연산을 계산한 결과가 같은 성질을 의미한다.

분배법칙 : 서로 다른 2가지 연산에 대해 다음의 규칙이 성립되는것.
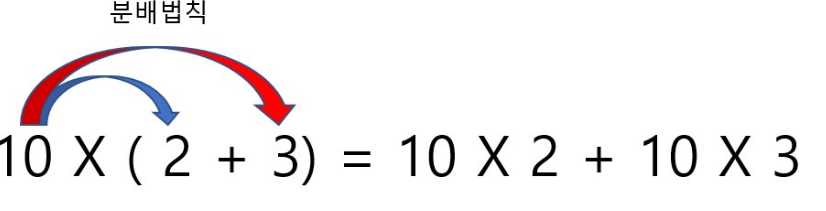
항등원(Identity) 이란 임의의 수와의 연산 결과를 항상 동일한 수로 만들어주는 특별한 수

덧셈의 항등원은 0이 되며, 곱의 항등원은 1이다.
역원(Inverse)이란 임의의 수와의 연산 결과를 항상 항등원으로 만들어주는 특별한 수다.
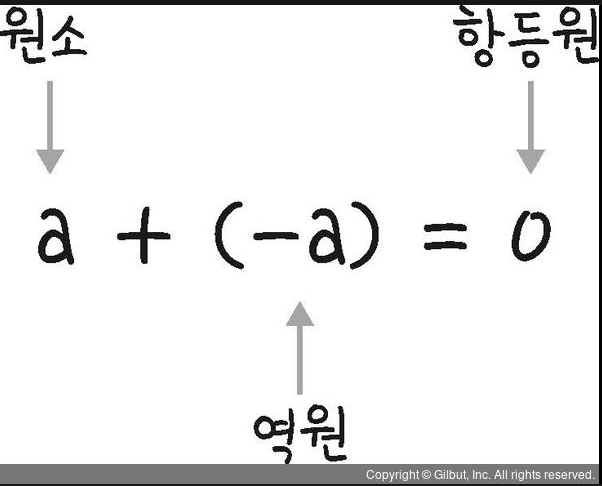
덧셈 역원은 주어진 수에서 항상 부호가 반대인 수가 되므로 반대수(Opposite number) 라고 부른다. 또한 곱셈의 역원은 분자가 1이고 분모는 주어진 수가 되며로 역수(Reciprocal) 이라고 한다.
닫혀 있음 : 어떤 집합에서 두 원소를 사용한 이항연산의 결과가 항상 그 집합에 속하는 성질
교환법칙 : 두 원소의 좌우 순서를 바꿔도 결과가 동일한 성질
결합법칙 : 새 원소의 연소순서를 바꿔도 결과가 동일한 성질
분배법칙 : 두 이상연산에 대해 a(b+c) = ab + ac 와 (b+c)a = b a + ca 의 결과가 나오는 성질
항등원 : 주어진 원소와의 이항연산 결과가 언제나 주어진 원소가 되는 특별한 원소,실수에서 덧셈의 항등원은 0이고 곱셈의 항등원은 1이다.
역원 : 주어진 원소와 이항연산결과가 언제나 항등원이 되는 특별한 원소, 실수에서 덧셈의 역원은 반대수, 곱셈의 역원은 역수 라고 한다.
2.12 수의구조
공리적 집합론에서 두 연산에 대해 1번부터 11번까지 공리를 모두 만족하는 집합은 체(Fleld)의 구조를 지난다고 표현한다
2.13 수의 표현
실수를 대응시켜 표한한 직선을 수직선(Number tine) 이라고 하며
또한 직각으로 만나는 직선을 의미하는 수직선(Perpendicular line)과 동음이다.
어떤 수의 원점으로부터의 거리는 구직 막대(Vertical bar) 기호를 써서 나타내는데, 이를 절대값(Absolute value)라고 한다.
2.2 함수
함수(Function)란 두 집합에서 첫 번쨰 집합의 모든 원소가 빠짐없이 두 번째 집합의 어떤 원소에 대응하는 관계를 말한다.
2.2.1 함수의 개념과 종류
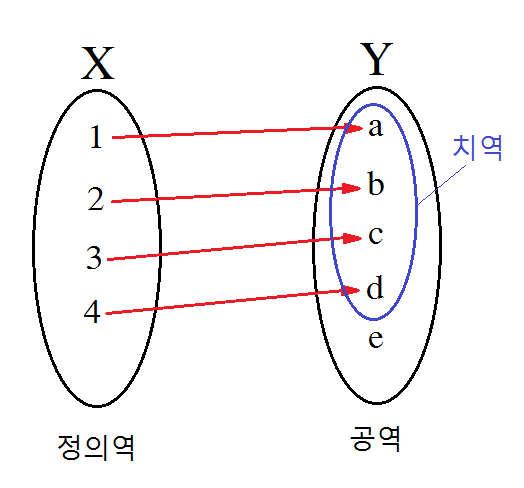
함수에서 왼쪽에 위치한 첫번째 집합을 정의역(Domain)이라고 하고, 도른쪽에 위치한 두 번쨰 집합을 공역(Codomain) 이라 한다.
정의역을 대응되는 공역의 원소만 따로 모아 부분집합(Sobset)을 형성할수 있는데, 이를 치역(Range)이라고 부른다.
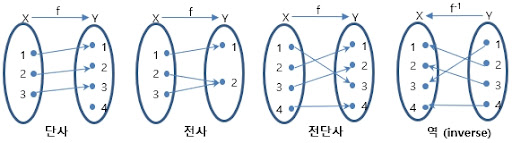
전사함수(Surjection)는 공역의 모든 요소가 정의역에 대응되는 함수를 의미한다.
단사함수(Injection)는 정의역과 공역의 요소가 일대일로 대응되는 함수를 의미한다.
전단사함수(Bijection)는 정의역과 공역의 모든 요소가 빠짐없이 일대일로 대응되는 함수를 의미한다.
2.2.2 합성함수
2개의 함수를 연쇄적으로 이어서 하나의 함수로 만드는 연산을 함수의 합성(Function composition)이라 한다.
2.2.3 항등함수와 역함수
정의역과 공역이 동일한 값으로 대응되는 함수를 항등함수(Identity function) 이라고 하며 기호 id로 나타낸다.
2.2.4 곱집합을 활용한 좌표 평면으로의 확장
곰집합(cartesian product) 이란 두 집합의 원소를 순서쌍으로 묶는 원소의 집합을 의미한다.
