210723 FUNDAMENTAL 16. Regression

1.선형회귀(Linear Regression)

• 왜 선형성이 보이기만 한다고 모두 선형 회귀가 아닐까?
  선형 회귀분석 조건 : 1)선형성 2)독립성 3)등분산성 4)정규성 5)

표현식
통계 : $y = \beta x + \epsilon$ ⇨ 머신러닝 : $H = Wx + b$

최소제곱법

• n 개의 점 데이터에 대하여 잔차의 제곱의 합을 최소로 하는 W, b를 구하는 방법
• 머신러닝에서는 회계 계수를 구하는 과정에서 손실함수(Loss function)을 사용
  • 즉, 최소제곱법이 손실함수 중에 하나의 방법임

경사하강법

• 적절한 회귀모델의 회귀계수를 찾기 ⇨ 손실함수를 최소화하는 $W$와 $b$를 구하는 것이 핵심!
  
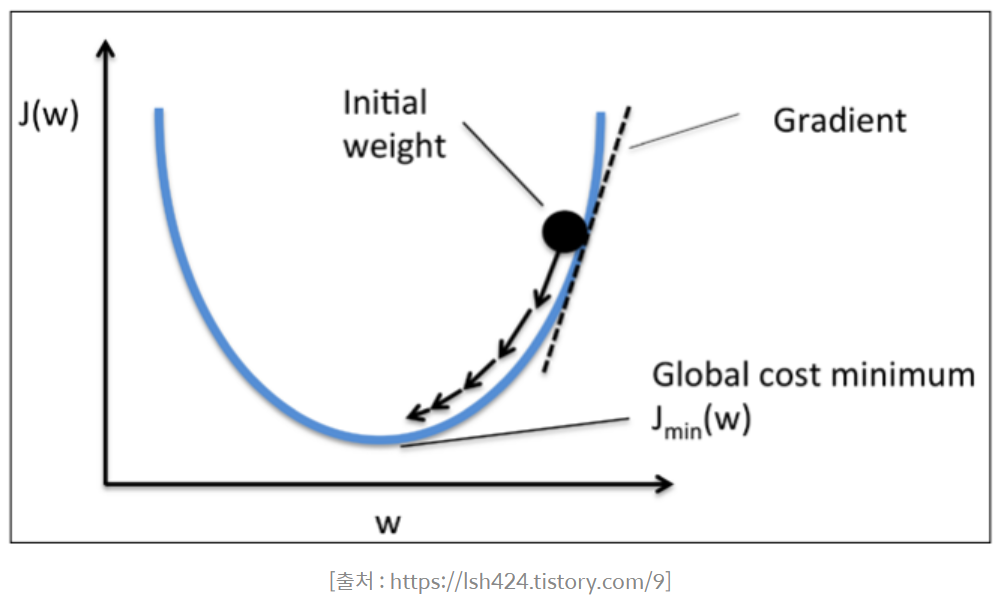
  가중치 파라미터의 개수가 많을 경우에는 어마어마한 시간이 걸리는 경우가 많기도 하고 무조건 최적의 가중치를 찾아낼 수 있는 것도 아니에요. 저 최소 지점으로 가기 위해, 그래디언트 값을 다음과 같은 식으로 업데이트를 한답니다.
  $W := W =\alpha \frac{\partial}{\partial W}J(W)$
  

2. 로지스틱 회귀분석(Logistic Regression)

• 분류 지도학습, 회귀 모델이지만 x가 어떤 범주에 속할 확률을 말해줌.
• Odds : 어떤 사건 A가 다른 사건 B 대비 발생할 확률
  $Odds = \frac{p}{1-p}$
• Logit = LogOdds
  $LogOdds = log(\frac{p}{1-p}) = \beta_0 + \sum_{j=1}^{p} \beta_j x_j$
  우리가 원하는 $p$d의 값으 얻으려면
  $$P(y=0|x) = \frac{}{} = f\frac{1}{1 + \exp(-z)} = Sigmoid Function

1. 실제 데이터를 대입하여 Odds 및 회귀계수를 구한다.
2. Log-odds를 계산한 후, 이를 sigmoid function의 입력으로 넣어서 특정 범주에 속할 확률 값을 계산한다.
3. 설정한 threshold에 맞추어 설정값 이상이면 1, 이하면 0으로 이진 분류를 수행한다.

이 함수는 확률모델을 선형 회귀모델로 표현한 것이 아니라, 위 그래프에서 $z=0$인 지점을 중심으로 하여 두 범주 간 경계가 불명확해지는 $x$의 구간$(0.3<p<0.7)$을 최소화해 주기 때문에 분류모델의 분류 성능을 매우 향상시켜 줍니다.

3. Softmax 함수와 Cross Entropy

1) Softmax 함수

• 2가지가 아닌 여러 범주로 분류하는 함수( = Multi class classification)

2) Cross Entropy

• softmax()의 손실함수로 사용
  • 즉, 가중치가 최적화될수록 H(p, q) 값이 감소
  • Why?
    • 선형회귀의 손실함수 = SSE(잔차제곱합) : 추정치와 실제값의 차이(거리 측정
    • L2 Distance : 두 점사의 거리
    • 모두 거리를 측정하기 적절한 형태
• cross entropy는 로지스틱 회귀 모델이 추론한 확률분포 $q(x)$와 실제 데이터의 분포 $p(x)$의 차이를 계산한 것.
  $Cross Entropy = q(x)-p(x)$

(이부분 수업내용 이해가 안되는 부분이라 다시 보고 정리 해볼 것!😉)

정리

	선형 회귀분석	로지스틱 회귀분석	다중 로지스틱 회귀분석
모형	- 종속변수가 연속형 - 독립변수 변화에 따른 종속변수 값 추정	- 종속변수의 범주가 2개 - 범주별 확률 추정 - 최대확률범주를 결정하는 분류모델로 활용	- 종속변수의 범주가 3개 이상
적용 함수	보편적으로 최소제곱법 이용	logits(=log-odds) sigmoid 함수	cross entropy 함수 softmax 함수
손실함수	보편적으로 최소제곱법 이용	cross entropy(class가 2개)	cross entropy