- 이미지 데이터의 채널(Channel): RBG, CHW(Channel, Width, Height)
- 신경망의 Weight = 레이어의 Weight가 더 정확!
1. Linear 레이어
- linear가 되기 위한 조건
- 모든 선들은 변환 이후에도 휘지 않고 직선이어야 함(곡선X)
- 원점은 변환 이후에도 여전히 원점이 여야 함(원점의 이동 X)
선형대수학이란?
행렬에 의해 변형된 공간에서 직선들은 평행을 유지하게 되는데 이것은 유클리드기하에서 다루는 기하학적인 구조이다. 따라서 선형대수학이란 행렬을 이용하여 이러한 구조를 대수적으로 계산하고 분석하는 학문
-
선형변환을 활용해 데이터를 특정 차원으로 변환하는 기능
ex) Fully Connected Layer, Feedforward Neural Network, Multilayer Perceptrons, Dense Layer... ⇨ 모두 Linear 레이어10차원 ←(데이터 집약)-- 100차원 --(데이터를 풍성하게)→ 300차원
-
Linear transformation = Linear function
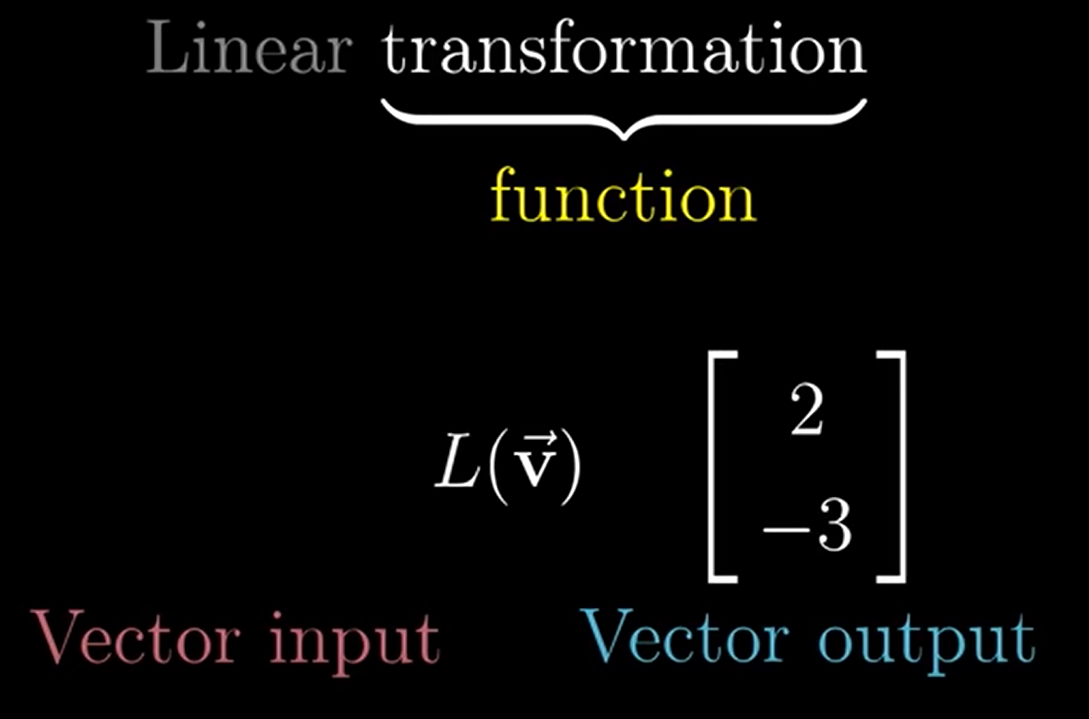
- 과적합(Overfitting)
- 훈련(Training) : Weight의 형태만 선언해주면 그 파라미터 값을 임의의 실수가 채우고, 수많은 데이터를 거치며 가장 적합한 Weight를 알아서 찾아가는 과정
- 편향(Bias) : 선형변환된 값에 편향 파라미터 b를 더해주는 것
2. Convolution 레이어
- 특징
- 이미지 입력을 처리할 때 Linear 레이어 대비 훨씬 적은 파라미터로 훨씬 효과적으로 중요한 이미지 피처를 뽑아낼 수 있음
- 정보 집약 효과 ⇨ 엣지, 특징들을 도드라지게 해줌
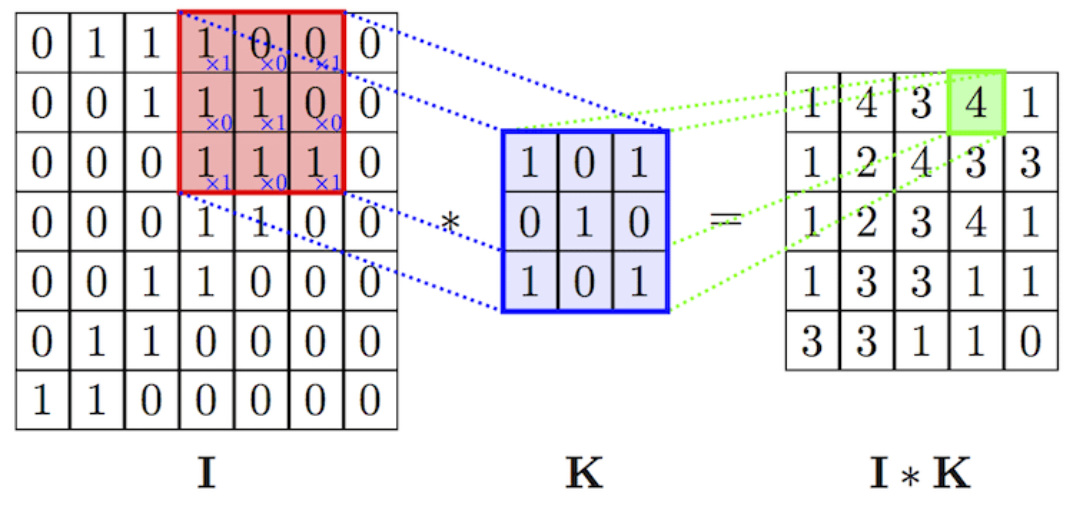
- convolution 연산 (ex. 사진 필터) : 입력의 형태를 변형시킨다
- 필터 = 커널(kernel)
- Stride : 필터를 적용 하는 간격 값
| Stride = 1 | Stride = 2 |
|---|---|
 | 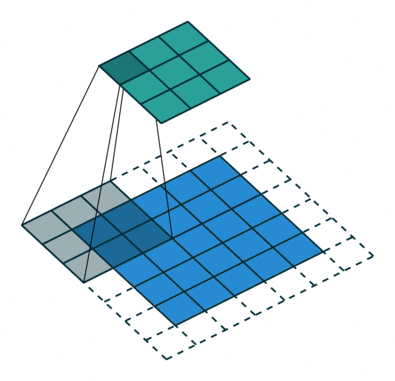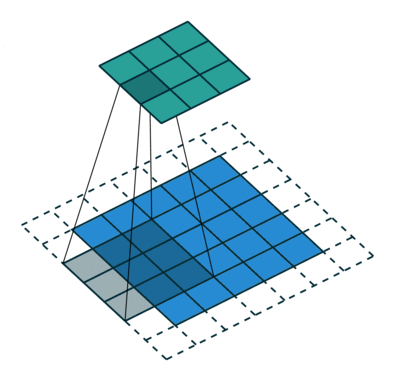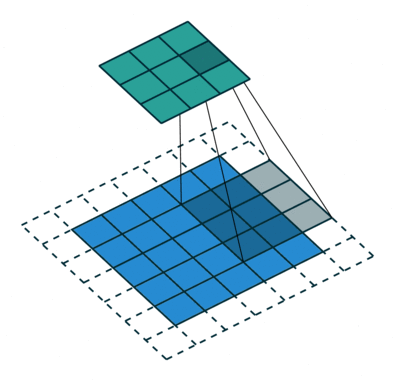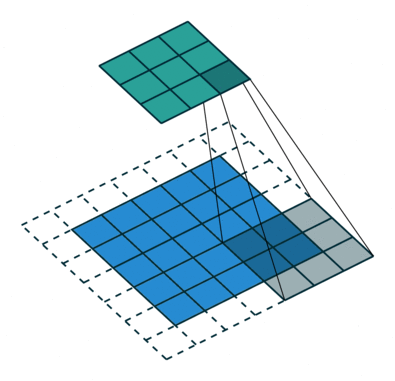 |
- Padding
- input 데이터를 convolutional 계산을 하는 과정에서 크기를 유지하는 것
- edge에 있는 값들도 내부에 있는 값들과 같은 횟수로 연산에 사용
CNN(Convlution Neural network 합성공 신경망)
Convolution 레이어에서 적은 수의 convolution filter를 통해 각 특징을 강화하여 이미지를 판별하는 인공신경망
DeepML Lec05 자료
3. Pooling 레이어
-
핵심남 추려서 더 특징을 확대
-
Receptive Field(수용영역)
Neural Network의 출력부가 충분한 정보를 얻기 위해 커버하는 입력 데이터의 Receptive Field가 충분히 커서 그 안에 detect해야 할 object의 특성이 충분히 포함되어 있어야 정확한 detection이 가능하게 됨 -
Max Pooling 레이어
효과적으로 Receptive Field를 키우고, 정보 집약 효과를 극대화할 수 있음 ⇨ 특징강화 -
효과
- translational invariance 효과 : object 위치에 대한 오버피팅을 방지하고 안정적인 특징 추출 효과를 가져옴 => Max Pooling을 사용하는 이유
- Non-linear 함수와 동일한 피처 추출 효과 : 분류기의 성능을 증진시키는 효과
- Receptive Field 극대화 효과
4. Deconvolution 레이어
-
집약된 정보의 복원
-
Convolution의 결과를 역재생해서 원본 이미지와 최대한 유사한 정보를 복원해 내는 Auto Encoder
-
dim(dimension) : 차원, 부피