210831 EXPLORATION 14. 시계열 예측

1. Time-Series : 시계열

• 시간 순서대로 발생한 데이터의 수열, $Y = {Y_t : t \in T}$ Where T is the index set

• 시간이 index 역할

  미래 데이터 예측 전제 사항

  1. 과거의 데이터에 일정한 패턴이 발견된다.
  2. 과거의 패턴은 미래에도 동일하게 반복될 것이다.
     ⇨ 안정적(Stationary) 데이터에 대해서만 미래 예측이 가능하다.

• 용어 정리(추가 정리 할 것!)

용어	수식	설명
분산 (Variance)
공분산 (Covariance)	$Cov(x, Y) = E((X-\mu)(Y-\nu))$	각 확률변수들이 어떻게 퍼져있는지를 나타내는 것
상관계수 (Correlation)
자기공분산 (Autocovariance)
자기상관계수 (Autocorrelation)
유의확률	귀무가설 유지될 확률?? 교수님 표현이 기억이 안난다...
가설검정
귀무가설$H_0$ (Null Hypothesis)
대립가설$H_1$ (Alternative Hypothesis)

2. Stationary Time-Series : 정상성

1) 안정적(Stationary)

• 시계열 데이터의 통계적 특성이 변하지 않음을 뜻함

  • 통계에서는 정상성이라고 표현함

• 대전제 : 과거의 패턴이 미래에도 반복될 것이다

• $t$에 무관하게 평균, 분산이 일정 범위안에 있어야 하고 일정 상관도를 가져야 예측이 가능함

• 통계적 특성(출처 : A Complete Tutorial on Time Series Modeling in R)

평균	분산	공분산

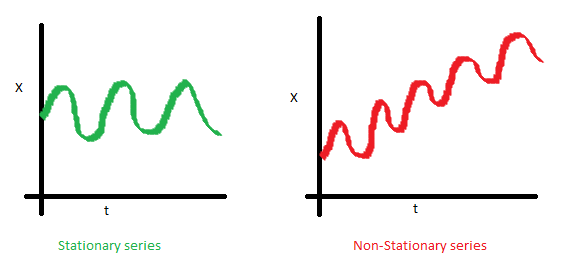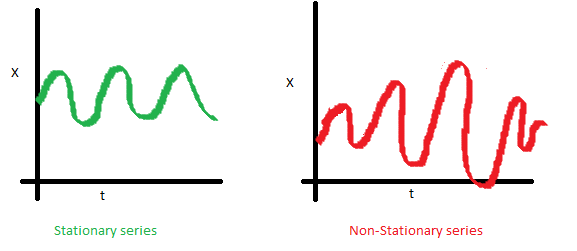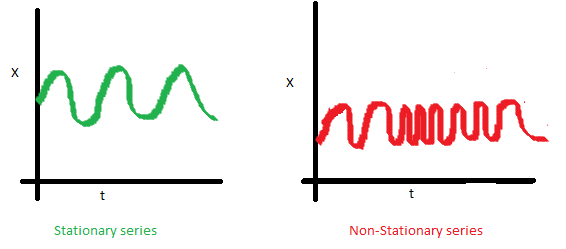2) 시계열 데이터에서 결측치 처리 방법

• 결측치 데이터 모두 삭제(drop)
• 결측치 보간(interpolate) 대입
  + ex) 2와 4 사이 데이터가 NaN이라면 이 값을 3으로 채우는 방식
  + 결측치 보간(interpolate)
  자료1, 자료2

3) non-stationary한 데이터를 stationary하게 만들기

1. 이동평균 모형 MA - tread 제거

2. 차분 Diff - seasonal 제거

3. 분해 Decomoisiotion - 추세/순환/계절/불규칙 요소로 분해
   

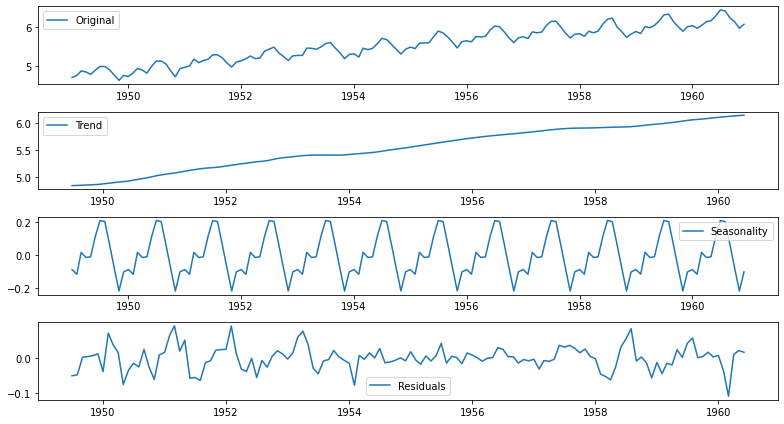
   	이동평균(MA)	차분(difference)	분해(decomposition)
   plot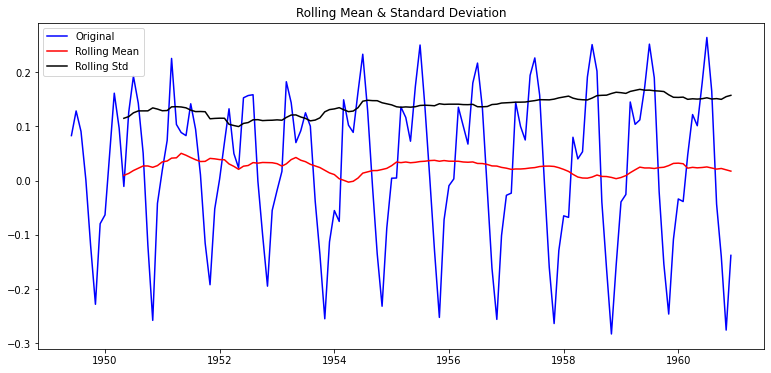
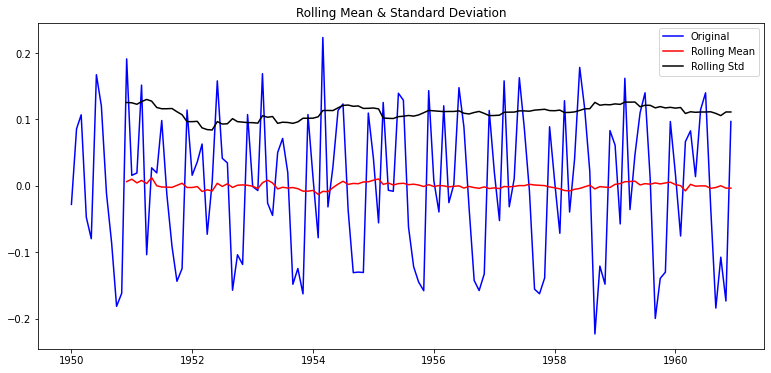
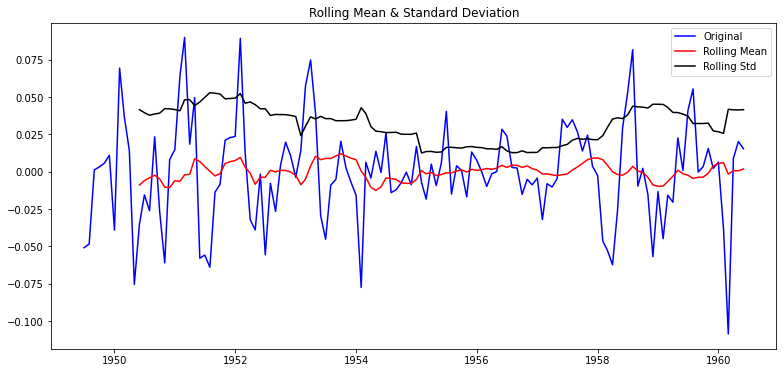
   p-value	0.180550	0.001941	2.885059e-08

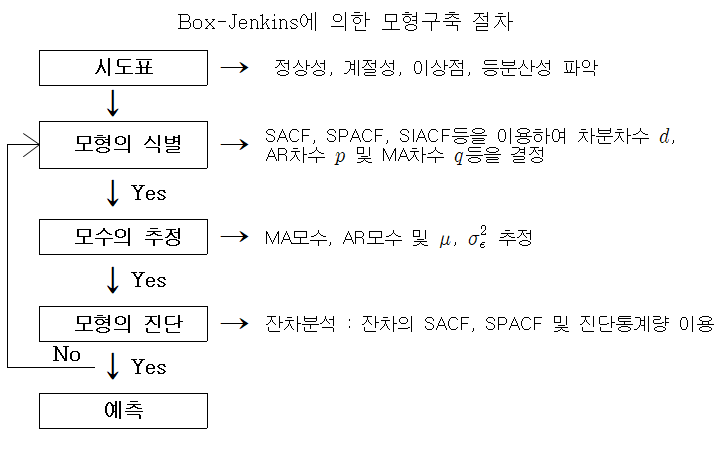
3. ARIMA(Box-Jenkins Technique)

• 정상성(stationary) 데이터에서 AR. MA, ARMA 모형 중에서 가장 적합한 모형을 선택해 줌
  • 자기상관계수(ACF)와 부분상과계수(PACF)를 분석하여 적절한 모형의 선택함
• ARIMA(p,d,q) = AR(Autoregressive) + I(Integrated) + MA(Moving Average)
  • p : 자기회귀 모형(AR)의 시차
  • q : 이동평균 모형(MA)의 시차
  • d : 차분누적(I) 횟수
• $Y = {Y_t : t \in T}$ 일 때 $Y_t$를 예측
• 장점
  • 단기예측의 정확성이 매우 높다.
  • 모형의 적합성을 검증할 수 있는 통계적 검진이 가능하다.
  • 예측의 신뢰구간설정이 가능하다.
• 단점
  • 상대적으로 많은 양의 데이터가 필요하다.
  • 새로운 데이터가 투입될 때 모형의 모수를 쉽게 업데이트할 수 있는 방법이 없다.
  • 만족스러운 모형을 개발하기 위해서는 많은 비용(시간과 자원)이 든다.

1) 자기상관계수(ACF) & 부분상과계수(PACF)

• ACF(Autocorrelation) : 시차(lag)에 따른 관측치들 사이의 관련성을 측정하는 함수
  $\rho(k) = \frac{Cov(Z_{t}, Z_{t+k})}{\sqrt{Var(Z_t)}\sqrt{Var(Z_{t+k})}}$
• PACF(Partial Autocorrelation) : 다른 관측치의 영향력을 배제하고 두 시차의 관측치 간 관련성을 측정하는 함수
  

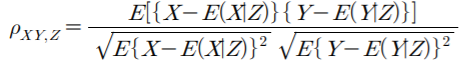
확률과정	ACF	PACF
AR(p)	지수곡선 또는 sin 곡선을 그리며 시차(k)가 증가함에 따라 0으로 급속히 감소(tails off)	시차(k)=p 이후 0으로 소멸/절단(cut off) 형태
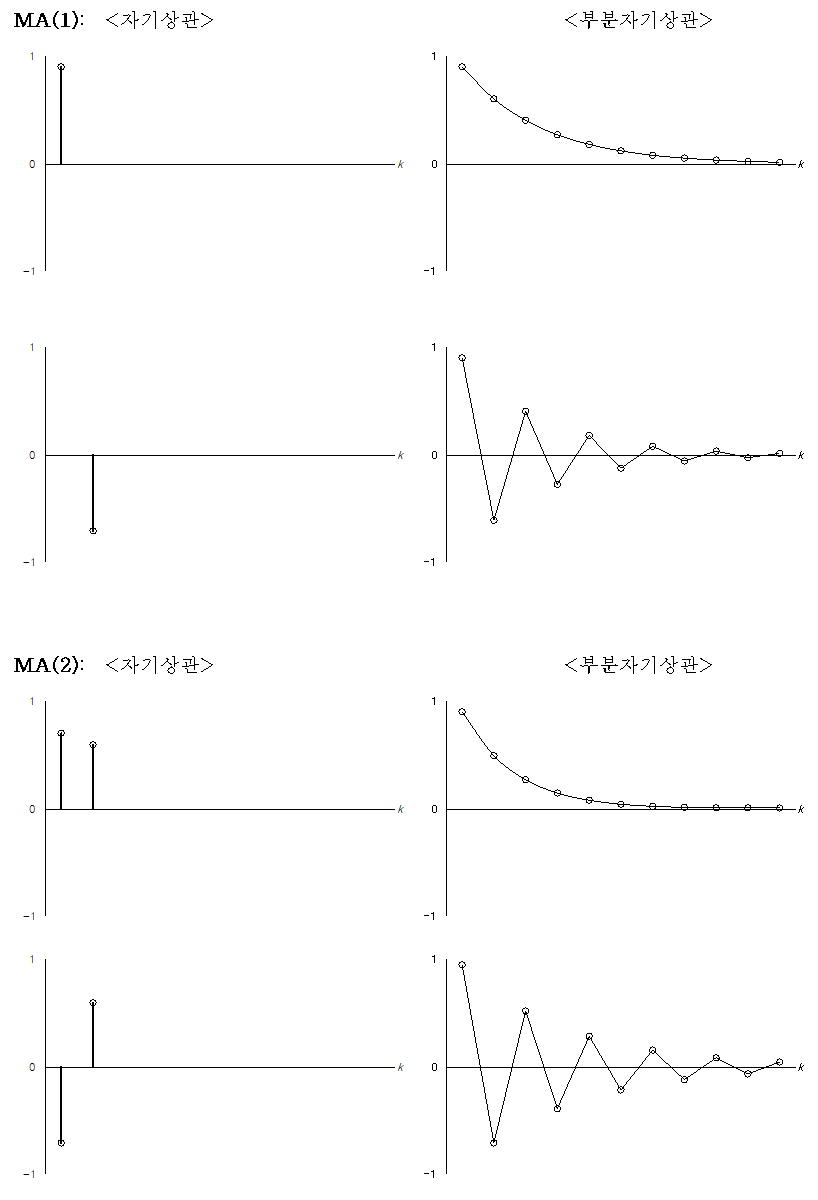
MA(q)	시차(k)=q 이후 0으로 소멸/절단(cut off) 형태	지수곡선 또는 sin 곡선을 그리며 시차(k)가 증가함에 따라 0으로 급속히 감소(tails off) 형태
ARMA(p,q)	시차(K)=q-p 이후에는 지수적으로 감소하거나 소멸하는 sin인함수 형태	시차(K)=q-p 이후에는 지수적으로 감소하거나 소멸하는 sin함수 형태
white noise	모든 시차에 대해 0	모든 시차에 대해 0

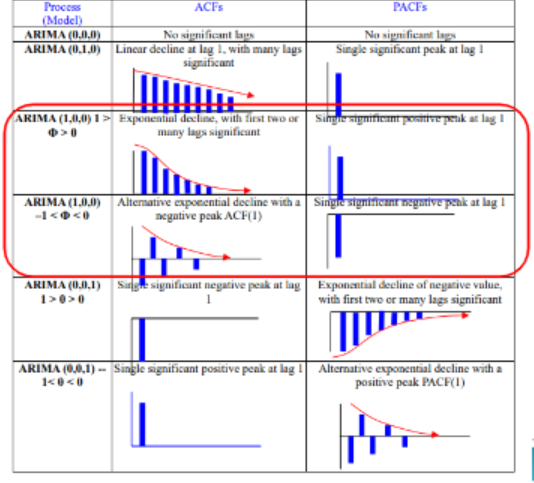
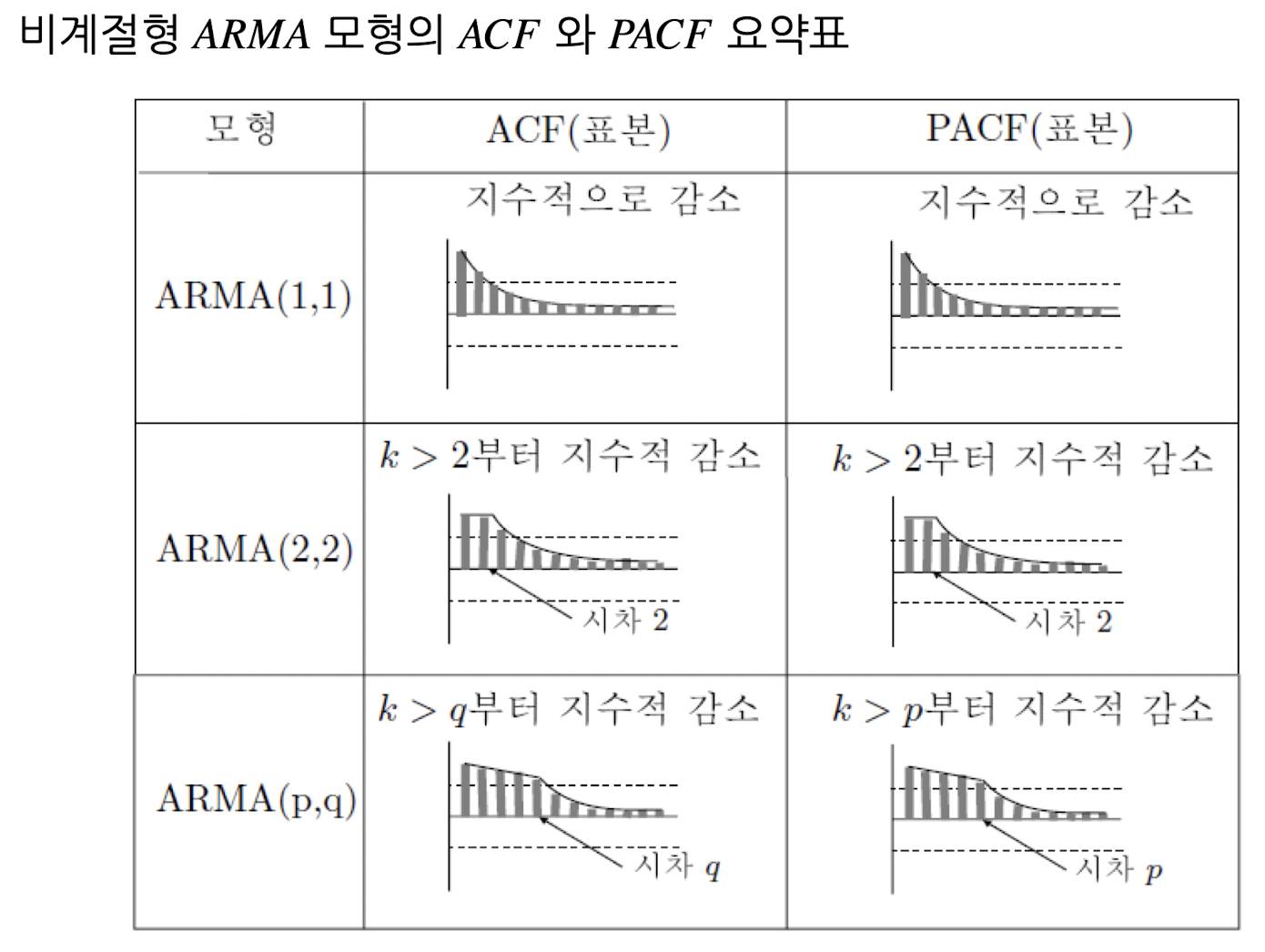
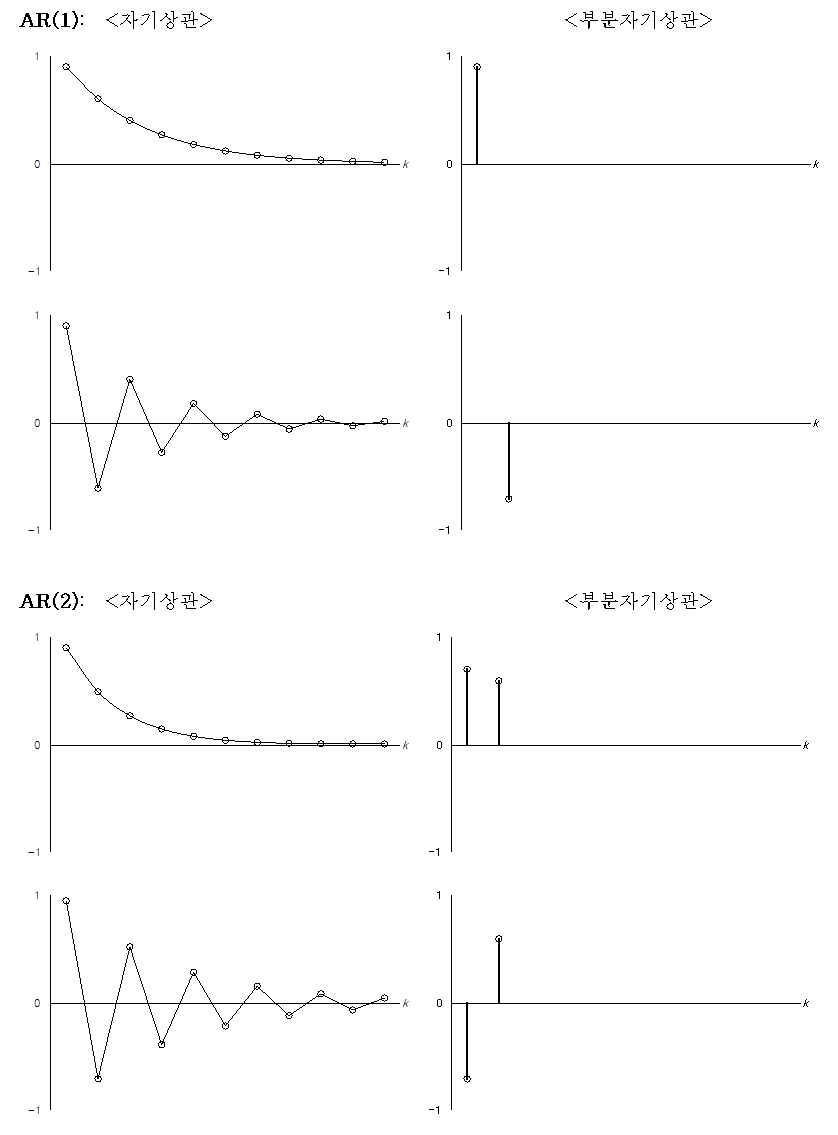
(그림 출처 : AR(AutoRegressive), MA(Moving Average), ARMA Models , ARIMA 모형 (비계절성) – 시계열분석)

2) 자기회귀(AR, Autoregressive)

• 과거 실제값들을 기반으로 미래 값을 예측하는 방법
• 잔차 Residual $\epsilon_t$에 대한 모델링
  ex) 주식값이 항상 일정한 균형 수준을 유지할 것이라고 예측하는 관점

$AR(p) = Y_t = \phi_0 + \phi_{1}Y_{t-1} + \phi_{2}Y_{t-2} + \dots + \phi_{p}Y_{t-p} + \epsilon_t$

$\phi_0 = \mu = c$ 자료마다 상수에 대한 표현의 차이가 있음

• 종속변수 $Y_t$
• 독립변수 $Y_{t-1}, Y_{t_2}, Y_{t_p}$
• 회귀계수 $\phi_0, \phi_1, \phi_p$
• 잔차(백색잡음) $\epsilon_t$

백색잡음(white noise)의 성질 :

• 잔차들($\epsilon_t$ | t=0, ±1 ····)간에 상관관계가 존재하지 않음
• $\epsilon_t$ ~ $iidN(0, \sigma_{\epsilon}^2)$

3) 이동평균(MA, Moving Average)

• 추세(Trend)에 해당하는 부분을 모델링
• 과거의 오차값들을 기반으로 미래를 예측하는 방법
  ex) 주식값이 최근의 증감 패턴을 지속할 것이라고 보는 관점

$MA(q) = Y_t = \epsilon_t - \theta_{1}\epsilon_{t-1} - \theta_{2}\epsilon_{t-2} - \dots - \theta_{q}\epsilon_{t-q}$

• 종속변수 $Y_t$
• 가중치 $\theta_0, \theta_{1}, \theta_{q}$
• 잔차의 이전 값 $\epsilon_{t-1}, \epsilon_{t-2}, \epsilon_{t-q}$
• 잔차 $\epsilon_t$
  

4) 차분누적(I, Integration)

• 계절성(Seasonality)에 해당하는 부분을 모델링
• $Y_t$이 이전 데이터와 $d$차 차분의 누적(integration) 합
• 차분 = 미분

5) ARMA

$Y_T = \phi_0 + \phi_{1}Y_{t-1} + \phi_{2}Y_{t-2} + \dots + \phi_{p}Y_{t-p} + \epsilon_t- \theta_{1}\epsilon_{t-1} - \theta_{2}\epsilon_{t-2} - \dots - \theta_{q}\epsilon_{t-q}$

4. 시계열 예측 지표 (MSE, MAE, RMSE, MAPE)

<읽기 자료> : 읽고 정리해볼 것
1. 히비스서커스의 블로그)
2. [Python 시계열 자료 분석] 시계열 모형의 예측 성능 평가 지표
3. R에서 예측 모형의 평가지표 구하기

---

💡 출처가 없는 것은 송준모교수님 시계열 분석 수업자료에서 가져옴
💡 도서 : Introductory Time Series with R(Springer)