• 유튜브 김성범[소장/]을 보고 정리하였습니다.

시계열 데이터

• 시계열 데이터 란?
  • 시간의 흐름에 따라 순서대로 관측되며 시간의 영향을 받는 데어터
  • Daily, Monthly, Quarterly, Yearly
• 구성 요소
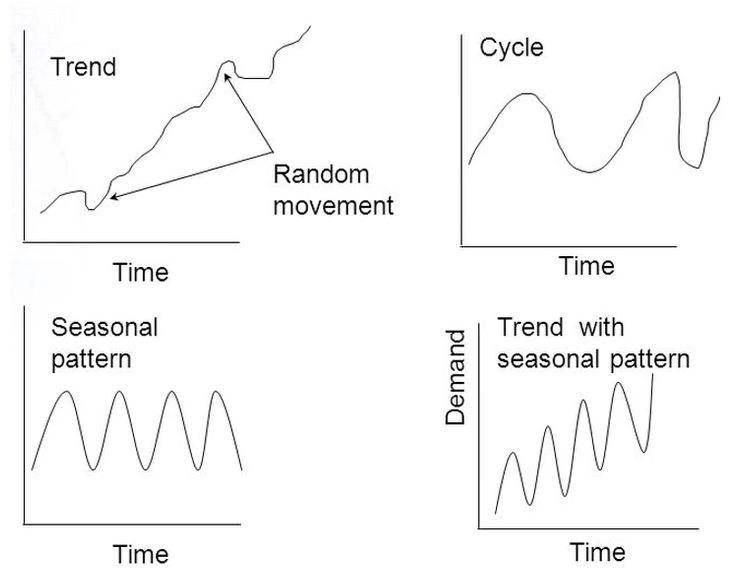
  • 추세 변동 Trend
    • 관측값이 지속적으로 증/감하는 변동
    • 특징 : 장기간(최소 1년 이상 지속)의 변동을 보임 ex) 경제
    • Downward/Upward 용어 주의
  • 순환 변동 Cycle $\supset$ 계절 변동 Seasonal variation
    • 주기적인 변화를 가지면서 계절에 의한 것이 아닌 주기가 긴 변동
    • 주기 : 주별, 월별, 계절별 등
  • 우연 변동 Random fluctuation
    • 시간에 따른 랜덤한 원이에 의한 변동(규칙적인 움직임과는 무관)
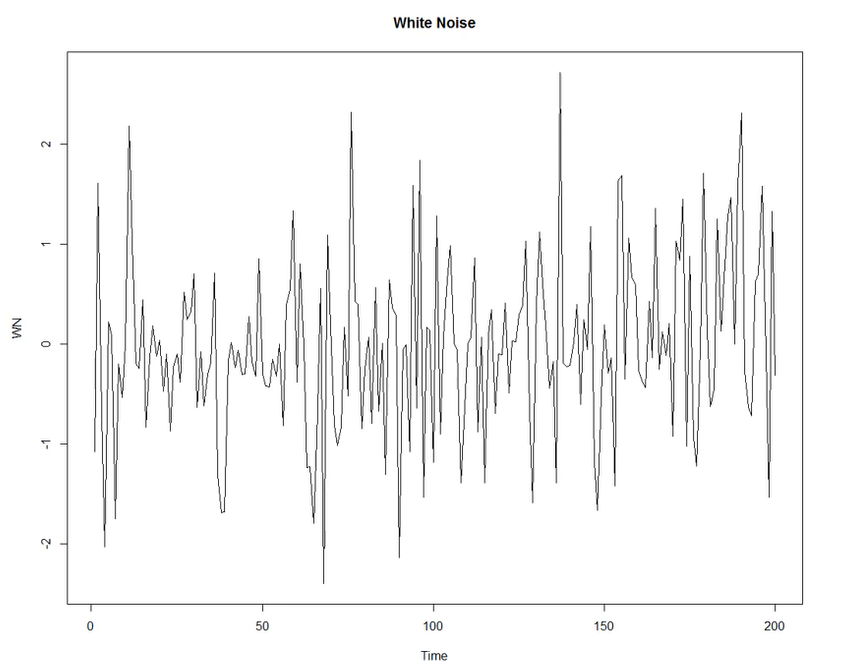
    • 대표 : 백색잡음 White Noise(평균 0, 분산이 일정한 ts data)

변동들의 예시	White Noise

시계열 예측 정확도 평가

1. 예측오차 Prediction error
   $e_t = y_t - \hat y_t$
   $\displaystyle\sum_{t=1}^n = y_t - \hat y_t$

   • $y_t$ : $t$시점에서 실제값, $\hat y_t$ : $t$시점에서 예측값
   • $e_t$가 작을 수록 모델을 제대로 만들었다고 할 수 있음
   • 단순한 정도/크기 차이(양수, 음수 부호는 중요하지 않음)

2. 평균 절대 편차(MAD : Mean Absloyte Deviation)

   • Absolyte Deviation : $|e_t| = |y_t - \hat y_t|$
   • MAD : $\frac{\displaystyle\sum_{t=1}^n |e_t|}{n} = \frac{\displaystyle\sum_{t=1}^n |y_t - \hat y_t|}{n}$

3. 평균 제곱 편차(MSE : Mean Squared Error)

   • Squared error : $(e_t)^2 = (y_t - \hat y_t)^2$
   • MSE : $\frac{\displaystyle\sum_{t=1}^n (e_t)^2}{n} = \frac{\displaystyle\sum_{t=1}^n (y_t - \hat y_t)^2}{n}$

	MAD	MSE
공통	음수를 양수로 만듦

4. MAPE (Mean Absolute Pecentage Error)
   $MAPE = \frac{\displaystyle\sum_{t=1}^n |\frac{y_t - \hat y_t}{y_t}|}{n} * 100$

• 단점
  • $y_t = 0$일때 정의가 되지 않는다 ?
  • 분모가 0에 가까울 수록, MAPE가 차이와 상관없이 무한으로 커짐
  • bias가 존재
    • $y_t > \hat y_t$ 일때, 호의 적인 경우가 있다. ?

https://white-joy.tistory.com/10