Cost function

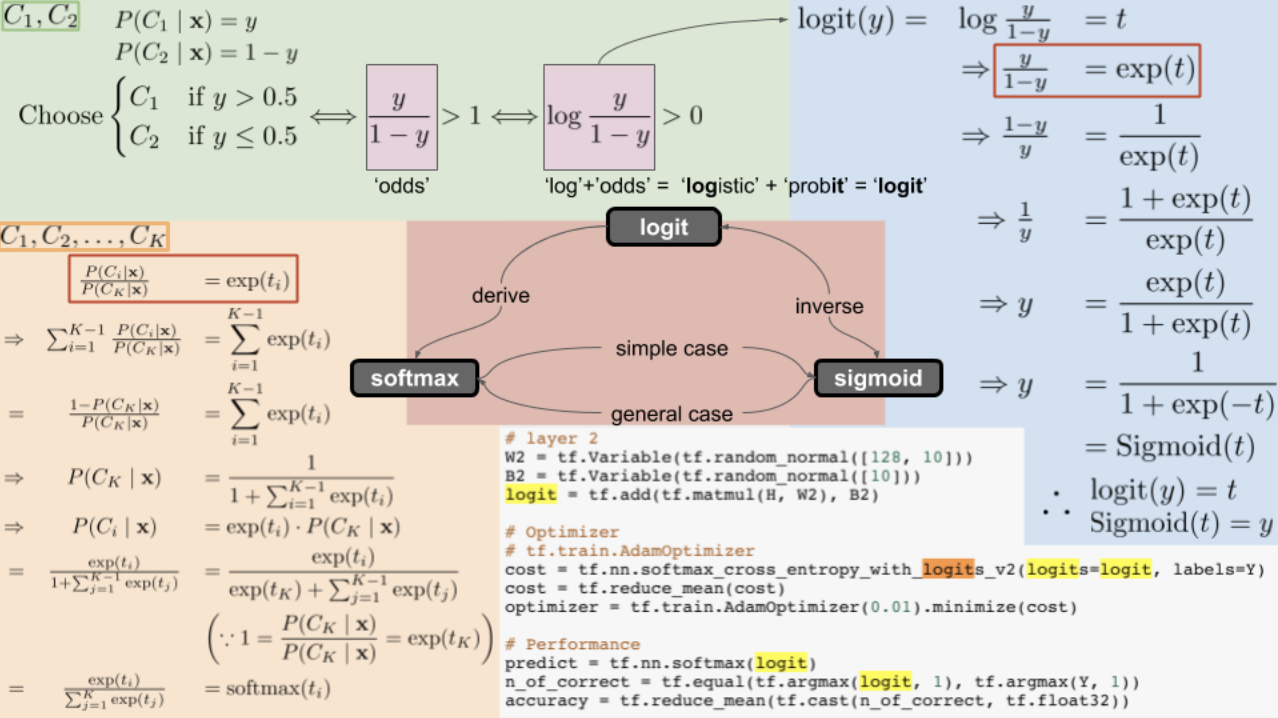
logit을 미분하면 softmax
softmax 적분하면 logit

logit과 sigmod 관계 = 역함수 inverse관계임.

그리고 logit = odds의 Log를 취한 것

참고자료 : logit, sigmoid, softmax의 관계,
https://opentutorials.org/module/3653/22995

파이토치로 선형 회귀 구현하기

MLP를 쓰지 않음

#데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])

#모델 초기화
W = torch.zeros(1, requires_grad=True)  # 1차원텐서, requires_grad는 자동미분하면서 결과값을 전부 기록해라!
b = torch.zeros(1, requires_grad=True)

# optimizer 설정
optimizer = optim.SGD([W, b], lr=0.01)

nb_epochs = 1999 # 원하는만큼 경사 하강법을 반복
for epoch in range(nb_epochs + 1):

# H(x) 계산
hypothesis = x_train * W + b           #우리가 목표로 하는 값.

# cost 계산
cost = torch.mean((hypothesis - y_train) ** 2) # MSE

# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward() # 역전파?
optimizer.step() #가중치 변화량 반영

# 100번마다 로그 출력
if epoch % 100 == 0:
    print('Epoch {:4d}/{} W: {:.3f}, b: {:.3f} Cost: {:.6f}'.format(
        epoch, nb_epochs, W.item(), b.item(), cost.item()
    ))

optimizer.zero_grad()가 필요한 이유

파이토치는 미분을 통해 얻은 기울기를 이전에 계산된 기울기 값에 누적시킨다.

   import torch
w = torch.tensor(2.0, requires_grad=True)

nb_epochs = 20
for epoch in range(nb_epochs + 1):

  z = 2*w

  z.backward()
  print('수식을 w로 미분한 값 : {}'.format(w.grad))
  
  

자동 미분(Autograd) 실습하기

w = torch.tensor(2.0, requires_grad=True)

 # 수식정리

y = w**2
z = 2*y + 5

# 해당 수식을 w에 대해서 미분. .backward()를 호출하면 해당 수식의 w에 대한 기울기를 자동으로 계산한다/

z.backward()

print('수식을 w로 미분한 값 : {}'.format(w.grad))

수식을 w로 미분한 값 : 8.0

nn Module로 구현하는 선형회귀

import torch.nn as nn
model = nn.Linear(input_dim, output_dim)

mport torch.nn.functional as F
cost = F.mse_loss(prediction, y_train)

위 예제에서는 직접 비용함수를 직접 정의해서 구현을 하였음. 그러나
파이토치에서는 선형 회귀 모델이 nn.Linear()라는 클래스?함수로, 또 평균 제곱오차가 nn.functional.mse_loss()라는 함수로 구현됨.

# 데이터 선언
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])
# 모델을 선언 및 초기화. 단순 선형 회귀이므로 input_dim=1, output_dim=1.

model = nn.Linear(1,1)

# model에는 가중치 W와 편향 b가 이미 저장되어 있다.. 이 값은 model.parameters() 함수를 써서 불로온다.

print(list(model.parameters()))

# 첫번째 값이 W고, 두번째 값이 b. 두 값 모두 현재는 랜덤 초기화 t상태임 
# 그리고 두 값 모두 학습의 대상이므로 requires_grad=True

# 옵티마이저를 정의 model.parameters()를 사용하여 W와 b를 전달 가능 학습률은 0.01

# optimizer 설정. 경사 하강법 SGD를 사용하고 learning rate를 의미하는 lr은 0.01
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

# 전체 훈련 데이터에 대해 경사 하강법을 2,000회 반복
nb_epochs = 2000
for epoch in range(nb_epochs+1):

# H(x) 계산
prediction = model(x_train)

# cost 계산
cost = F.mse_loss(prediction, y_train) # <== 파이토치에서 제공하는 평균 제곱 오차 함수

# cost로 H(x) 개선하는 부분
# gradient를 0으로 초기화
optimizer.zero_grad()
# 비용 함수를 미분하여 gradient 계산
cost.backward() # backward 연산
# W와 b를 업데이트
optimizer.step()

if epoch % 100 == 0:
# 100번마다 로그 출력
  print('Epoch {:4d}/{} Cost: {:.6f}'.format(
      epoch, nb_epochs, cost.item()
  ))
  
  # W , B 값 확인하기
  
  print(list(model.parameters()))
  

Class로 구현하는 선형회귀

class LinearRegressionModel(nn.Module): # torch.nn.Module을 상속받는 파이썬 클래스
    def __init__(self): # 생성자 호출
        super().__init__()  # 부모클래스
        self.linear = nn.Linear(1, 1) # 단순 선형 회귀이므로 input_dim=1, output_dim=1. # self.linear 라는 필드로 채워놓기

    def forward(self, x): x라는 값을 인자로 받아서 linear field에 있는 값을 x값으로 넣어서 호출?? 그 결과값이 리턴 
        return self.linear(x)
       
    model = LinearRegressionModel()
    
    # 전체 훈련 데이터에 대해 경사 하강법을 2,000회 반복
nb_epochs = 2000

for epoch in range(nb_epochs+1):

# H(x) 계산
prediction = model(x_train)

# cost 계산
cost = F.mse_loss(prediction, y_train) # <== 파이토치에서 제공하는 평균 제곱 오차 함수

# cost로 H(x) 개선하는 부분
# gradient를 0으로 초기화
optimizer.zero_grad()
# 비용 함수를 미분하여 gradient 계산
cost.backward() # backward 연산
# W와 b를 업데이트
optimizer.step()

if epoch % 100 == 0:
# 100번마다 로그 출력
  print('Epoch {:4d}/{} Cost: {:.6f}'.format(
      epoch, nb_epochs, cost.item()
  ))

forward() 함수는 model 객체를 데이터와 함께 호출하면 자동으로 실행된다. 예를 들어 model이란 이름의 객체를 생성 후, model(입력 데이터)와 같은 형식으로 객체를 호출하면 자동으로 forward 연산이 수행이됨 == 콜백함수 콜백 method!!