지난 시간 복습

선형 회귀 모델의 가설식은 H(x) = Wx + b 였다.
그리고 이 가설식을 구현하기 위해서 파이토치의 nn.Linear()를 사용했따. 그리고 로지스틱 회귀의 가설식은 H(x) = sigmoid(Wx+B).
파이토치에서는 nn.Sigmoid()를 통해서 시그모이드 함수를 구현하므로 결과적으로 nn.Linear()의 결과를 nn.Sigmoid()를 거치게하면 로지스틱 회귀의 가설식이 된다ㅓ.

모델을 class로 구현하기

1. 클래스(class) 형태의 모델은 nn.Module 을 상속받는다. 그리고 init()에서 모델의 구조와 동적을 정의하는 생성자를 정의한다. 이는 파이썬에서 객체가 갖는 속성값을 초기화하는 역할로, 객체가 생성될 때 자동으호 호출된다.
2. super() 함수를 부르면 여기서 만든 클래스는 nn.Module 클래스의 속성들을 가지고 초기화된다,
3. foward() 함수는 모델이 학습데이터를 입력받아서 forward 연산을 진행시키는 함수이다. 이 forward() 함수는 model 객체를 데이터와 함께 호출하면 자동으로 실행이된다.
4. 예를 들어 model이란 이름의 객체를 생성 후, model(입력 데이터)와 같은 형식으로 객체를 호출하면 자동으로 forward 연산이 수행된다.

Mini Batch

전체 데이터를 더 작은 단위로 나누어서 해당 단위로 학습하는 개념이 나오게 됨. 이 단위를 미니 배치라함

-1 epoch를 여러 번의 mini-batch로 나눠서 학습

• 메모리 요구량이 줄어듬

-10 epoch / mini-batch X != 10 epoch / mini-batch 10

• 다름

-10 epoch+mini-batch 10 = 100 epoch with batch사이즈(한 번에 다처리)

• 동일

파이토치에서는 데이터를 좀 더 쉽게 다룰 수 있도록 유용한 도구로서 데이터셋, 데이터로더를 제공한다. 이를 사용하면 미니 배치 학습, 데이터 셔플(shuffle), 병렬 처리까지 간단히 수행 가능하다.

Logistic Regression 그려보기

직접 그려보기

%matplotlib inline
import numpy as np # 넘파이 사용
import matplotlib.pyplot as plt # 맷플롯립사용


def sigmoid(x): # 시그모이드 함수 정의
return 1/(1+np.exp(-x))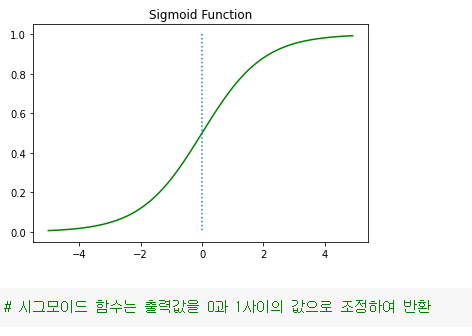

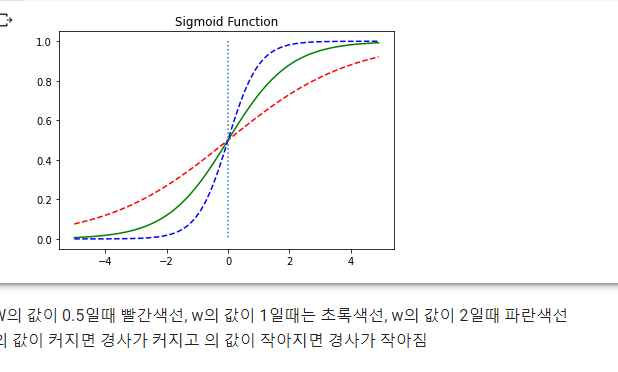
W값의 변화에 따른 경사도 변화

		x = np.arange(-5.0, 5.0, 0.1)

y1 = sigmoid(0.5x)
y2 = sigmoid(x)
y3 = sigmoid(2x)

plt.plot(x, y1, 'r', linestyle='--') # W의 값이 0.5일때
plt.plot(x, y2, 'g') # W의 값이 1일때
plt.plot(x, y3, 'b', linestyle='--') # W의 값이 2일때
plt.plot([0,0],[1.0,0.0], ':') # 가운데 점선 추가
plt.title('Sigmoid Function')
plt.show()

파이토치로 로지스틱 회귀 구현하기

x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_data = [[0], [0], [0], [1], [1], [1]]
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)

# 모델 초기화

W = torch.zeros((2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

optimizer 설정

optimizer = optim.SGD([W, b], lr=1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):

# Cost 계산
hypothesis = torch.sigmoid(x_train.matmul(W) + b)
cost = -(y_train * torch.log(hypothesis) + 
         (1 - y_train) * torch.log(1 - hypothesis)).mean()

# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()

# 100번마다 로그 출력
if epoch % 100 == 0:
    print('Epoch {:4d}/{} Cost: {:.6f}'.format(
        epoch, nb_epochs, cost.item()
    ))
    

Epoch 0/1000 Cost: 0.693147
생략
Epoch 1000/1000 Cost: 0.019852

hypothesis = torch.sigmoid(x_train.matmul(W) + b) #  W와 b를 가지고 예측값을 출력
print(hypothesis)

>tensor([[2.7648e-04],
        [3.1608e-02],
        [3.8977e-02],
        [9.5622e-01],
        [9.9823e-01],
        [9.9969e-01]], grad_fn=<SigmoidBackward0>)
prediction = hypothesis >= torch.FloatTensor([0.5])
print(prediction)

# 위 값들은 0과 1 사이의 값을 가지고 있다. 
# 0.5넘으면 True, 넘지 않으면 False로 값을 정하여 출력해보자....
tensor([[False],
    [False],
    [False],
    [ True],
    [ True],
    [ True]])