DFS/BFS 알고리즘

1 DFS/BFS란 무엇인가?

DFS : 그래프를 깊이우선으로 탐색하는 알고리즘이다.
BFS : 그래프를 너비우선으로 탐색하는 알고리즘이다.

탐색문제 유형

경로탐색 유형 (최단거리, 시간)
a~b지점까지 가는데 최소 거리/최단 시간 구하기

네트워크 유형 (연결)
여러 개체들이 주어진 상태에서 연결되어 있는 그룹의 개수를 구하거나 두 개체가 같은 네트워크 안에서 연결되어 있는지 확인하기

조합 유형 (모든 조합 만들기)
여러가지의 조합을 모두 만들고 비교하기

DFS (Depth First Search : 깊이 우선 탐색)

재귀함수를 이용한 방법, stack을 이용한 방법이 있는데
보통 재귀가 간결하기때문에 재귀함수를 이용한다.
방향이 정해지면 끝까지 가기때문에 그래프에서 사이클을 찾는데 유용하게 이용된다.
깊이를 우선적으로 탐색할때자주 쓰인다.

const DFS = (graph, startNode) => {
  const visited = []; // 탐색을 마친 노드들
  let visitTable = []; // 탐색해야할 노드들

  visitTable.push(startNode); // 노드 탐색 시작

  while (visitTable.length !== 0) { // 탐색해야할 노드가 남아있다면
    const node = visitTable.shift(); // queue이기 때문에 선입선출, shift()를 사용한다.
    if (!visited.includes(node)) { // 해당 노드가 탐색된 적 없다면
      visited.push(node); 
      visitTable = [...graph[node], ...visitTable];
    }
  }
  return visited;
};

BFS (breadth first search : 넓이 우선 탐색)

기본조건은 DFS와 유사하나 시작노드의 기준으로부터 인접노드들을 탐색한다.
마치 물결처럼 퍼져나가는 진행방식이다. 목적지의 반대방향을 탐색하더라도
끝까지 탐색을 하기때문에 최단거리를 보장할수는 없다.

const BFS = (graph, startNode) => {
  let visited = []; // 탐색을 마친 노드들
  let visitTable = []; // 탐색해야할 노드들

  visitTable.push(startNode); // 노드 탐색 시작

  while (visitTable.length !== 0) { // 탐색해야할 노드가 남아있다면
    const node = visitTable.shift(); // 가장 오래 남아있던 정점을 뽑아냄.
    if (!visited.includes(node)) { // 해당 노드 방문이 처음이라면,
      visited.push(node); 
      visitTable = [...visitTable, ...graph[node]];
    }
  }
  return visited;
};

트리를 순회할때 진행 방향을 보면 이해하기 쉽다.

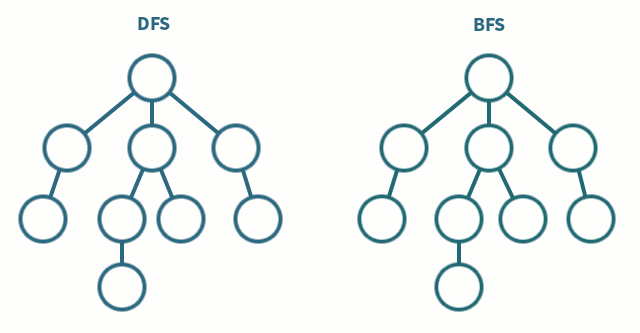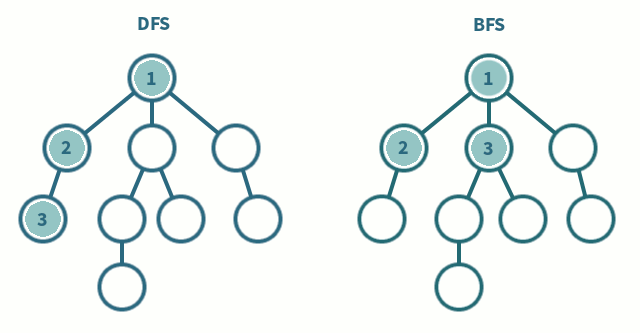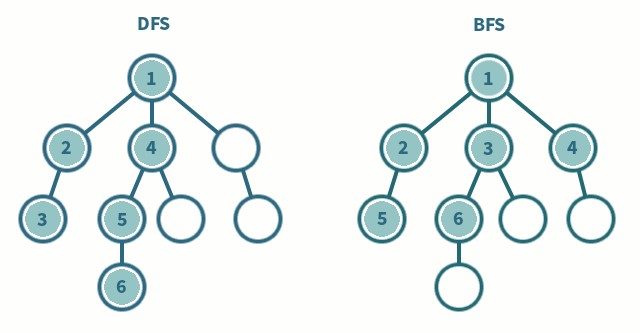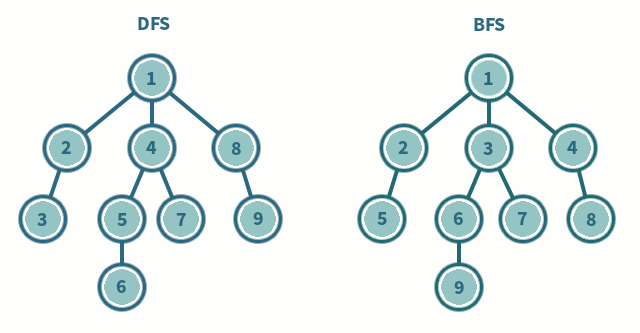
상황에 따라서 bfs/dfs 의 성능차이가 갈릴수도있으니
상황에 맞게 쓰는게 중요하다.