data structures - union find

출처

유니온 파인드란 무엇인가?

대표적인 그래프 알고리즘이며, 두 노드가 같은 집합에 있는지 판별하는 알고리즘이다
disjoint=set 이라고도 부른다.
단계는 총 3단계이며
1. make-set (각 노드를 초기화시켜준다.)
2. find (각노드의 루트노드를 찾는다.)
3. union (노드를 합친다.)

//  make-set단계) 노드를 표현할 배열을 만들어준후에 초기화시켜준다.
let parent = new Array(n)
for (let i = 0; i <= n; i++) {
  parent[i] = i
}

//  find단계) 노드의 루트노드(부모노드)를 찾는다.
function find(x){
  if(parent[x] === x){
    return x
  }else{
    return find(parent[x])
  }
}

union 함수에서는 사이즈에 기반한 union by rank 기법을 사용할 수 있다. 핵심 원리는 더 큰 트리 밑에 더 작은 트리를 붙이는 것이다. 따라서 루트 요소가 나타내는 음수에 기반해서 더 작은 트리의 부모 인덱스를 더 큰 트리의 루트로 교체한다. 트리를 붙이면 병합 당하는 쪽은 깊이가 한 칸 깊어지는데, 당연히 하나라도 깊이가 덜 깊어지는 편이 효율적이기 때문에 작은 트리를 큰 트리 밑에 붙이는 것이다. rank를 깊이로 설정할 수도 있는데 그 경우도 당연히 깊이가 더 깊은 루트에 얕은 트리를 붙이면 트리가 더 깊어지는 것을 최소화할 수 있을 것이다.

// union단계) 각 간선의 부모노드를 찾고 노드간 연결시켜준다.
function union(a,b){
  let rootA = find(a)
  let rootB = find(b)
  if(rootA === rootB)return
  if(rootA < rootB){
    parent[rootB] = rootA
  }else{
    parent[rootA] = rootB
  }
}

find 함수에서 최적화할 부분은, 재귀적으로 부모 인덱스를 따라 가는 동시에 최종적으로 발견되는 부모 인덱스로 경로 상의 모든 인덱스를 갱신하는 것이다. 이렇게 하면 나중에는 이 경로를 다 따라가지 않고 바로 루트를 발견할 수 있다. 이 기법을 path compression이라고 한다 이러한 방법으로 시간복잡도를 단축할수있다.

function find(x){
  if(parent[x] === x){
    return x
  }else{
    return parent[x] = find(parent[x])
  }
}

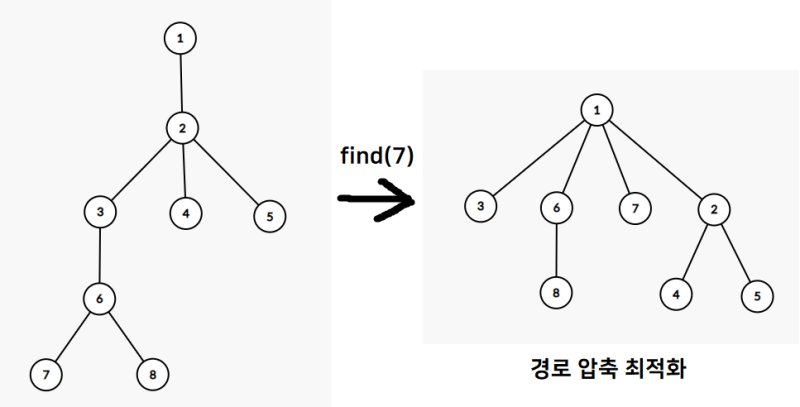
path compression

구성은 간단하지만 이해하는데 시간을 상단시간 투자했던것같다.