m-Coloring

m-Coloring 문제는 undirected-graph에서 서로 인접한 정점이 같은 색을 갖지 않도록 최대 m개의 다른 색으로 칠하는 방법을 모두 찾는 문제입니다.
그 중 칠할 수 있는 색깔이 최소인 경우의 m과 해당 경우의 모든 색칠 방법의 수를 찾는 문제로 약간 변형하여 풀어보았습니다.

생각 1

먼저 위 사진과 같이 어릴 때 자주 풀어봤던 지도 색칠하기 문제를 graph로 나타내어 봅시다.

graph는 undirected일 수 밖에 없으며 간선마다 가중치가 따로 없습니다.
인접한 v1-v3 간선은 True(1)로 나타내고 인접하지 않는 v1-v5 간선은 False(0)로 나타낼 수 있습니다.

따라서 이를 adjacency matrix(인접 행렬)의 방식으로 나타냅니다.

이를 graph로 나타내었기 때문에 전체를 탐색하는 Brute-Force한 방법으로 해결해보자는 생각을 하였습니다.

전체를 탐색하기 위해 SST(State-Space-Tree)로 나타내어 생각할 수 있습니다.
다음 단계로 BFS로 전체의 모든 경우를 탐색할 수 있습니다.

생각 2

하지만 위와 같은 전체 탐색은 불필요 합니다.

v1에 특정 색이 칠해졌는데 다음 인접 노드인 v2에서 같은 색깔을 칠한다면 이후 노드들은 볼꺼 없이 solution이 될 수 없기 때문입니다.

따라서 이들의 경우 promising()을 통해 pruning하는 Backtracking 기법을 사용하여 걸러내어 줍니다.

이러한 방식이면 SST가 다음과 같이 그릴 수 있습니다.

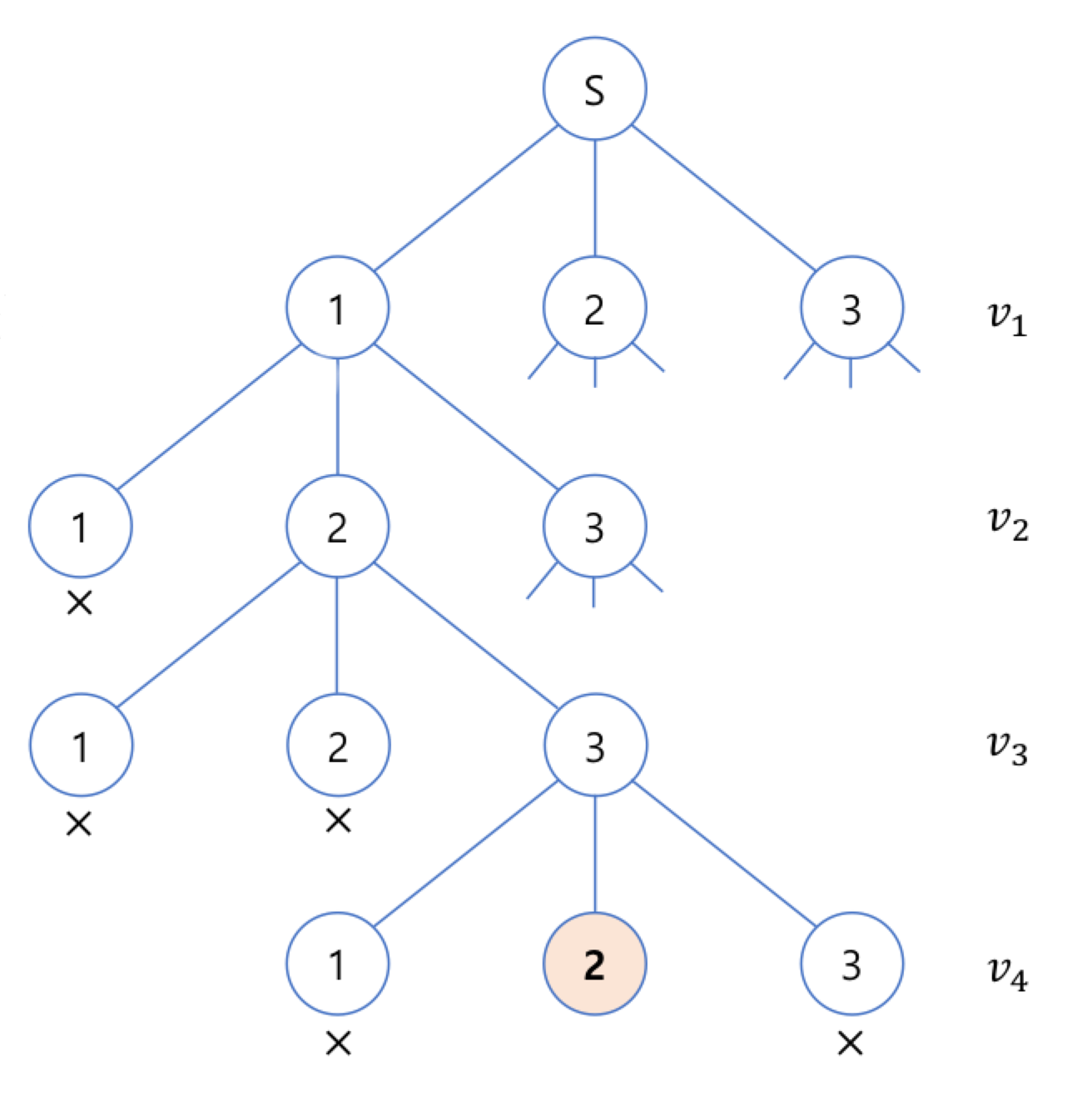
총 칠할 수 있는 색의 개수를 3개라고 한다면, 색깔의 종류는 1, 2, 3이 있습니다.

각 노드에 어떤 색일 칠할 지 결정하기 위한 list를 만들고 내부에 현재의 색깔을 저장합니다.

그림의 경우 [0, 0, 0, 0, 0] 이렇게 됩니다.
각 노드가 1번부터 시작이기 때문에 헷갈림 방지를 위해 0번 노드도 추가해주었습니다.

그림처럼 [0, 1, 2, 3, 2] 일 경우 성공입니다.
인접한 노드의 색깔이 모두 다릅니다.

구현

def m_coloring(i):
    global count # 현재 발견한 solution 개수
    global m # 현재 사용 색깔 개수
    # 탐색
    if promising(i):
        if i == n: # 끝까지 탐색 -> 정답
            count+=1
        else:
            for color in range(1, m + 1): # 모든 가능 색깔 탐색
                vcolor[i + 1] = color
                m_coloring(i + 1) # 다음 재귀로 넘어가고 불가능하다면 backTracking

m-coloring()에서는 promising()에 의해 걸러지지 않은 경우에만 다음 vertex의 경우를 판단 할 수 있게 구현합니다.
이를 통해 전체 탐색하던 방식에서 유망한 경우만을 탐색하여 시간복잡도를 줄일 수 있습니다.

def promising(i):
    j = 1 #SST를 탐색
    flag = True

    while j < i and flag:
        if W[i][j] and vcolor[i] == vcolor[j]: #W[i][j]가 연결되어 있으며, 두 노드의 색깔이 같다면
            flag = False
        j += 1
    return flag

promising()에서는 SST를 탐색하는데 연결 여부와 연결되었다면 색깔 동일 여부를 판단합니다.
연결되지 않았다면 탐색할 필요가 없고 또한 색깔이 같다면 탐색 할 필요가 없습니다.

전체 소스 코드입니다.

def m_coloring(i):
    global count # 현재 발견한 solution 개수
    global m # 현재 사용 색깔 개수
    # 탐색
    if promising(i):
        if i == n: # 끝까지 탐색 -> 정답
            count+=1
        else:
            for color in range(1, m + 1): # 모든 가능 색깔 탐색
                vcolor[i + 1] = color
                m_coloring(i + 1) # 다음 재귀로 넘어가고 불가능하다면 backTracking
                
 

def promising(i):
    j = 1 #SST를 탐색
    flag = True

    while j < i and flag:
        if W[i][j] and vcolor[i] == vcolor[j]: #W[i][j]가 연결되어 있으며, 두 노드의 색깔이 같다면
            flag = False
        j += 1
    return flag



#input
n ,k = map(int, input().split())

W = [[0]*(n + 1) for _ in range(n + 1)]

for _ in range(k):
    a,b = map(int, input().split())
    W[a][b] = 1
    W[b][a] = 1

m = 1 # color 개수
vcolor = [0]*(n + 1) #노드 개수 (0, 1번, 2번, 3번, ... n번)
while True:
    count = 0
    m_coloring(0) #return count
    if count >=1 :
        break
    else: m += 1

print(m, count, sep="\n")

감사합니다.😀