The Sum-of-Subsets Probrem

양의 정수 n개가 존재하는 집합 w의 부분집합 중 모든 원소를 합해서 W
가 되는 모든 부분 집합을 찾는 문제입니다.

생각 1

우선적으로 집합의 모든 부분집합을 생각해봅니다.

해당 원소가 부분집합에 포함되냐 포함되지 않느냐에 따라 2가지 경우로 나눌 수 있습니다.
원소가 4개인 집합의 부분집합 SST(Space-Sub-Tree)를 그려본다면 다음과 같습니다.

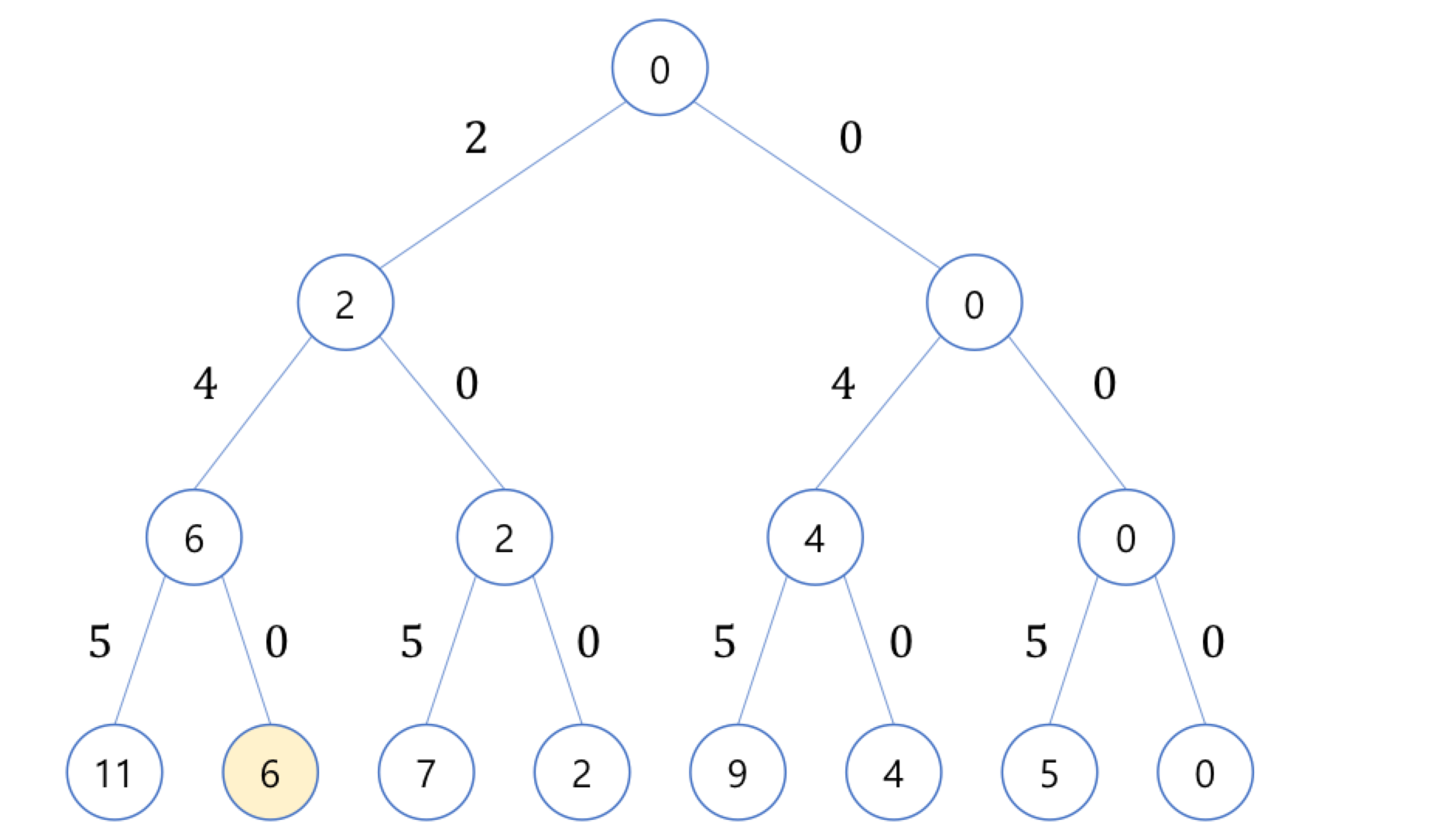
총 노드의 개수는 1 + 2^0 + 2^1 + 2^2 + 2^3 + 2^4 = 2^5-1 이며 해당 노드들을 모두 탐색할 경우 즉 Brute-Force하게 구현하였을 경우 O(2^n)의 factorial time에 원하는 결과값을 도출할 수 있습니다.

생각 2

해당 시간을 줄이기 위해서는 BackTracking 방식을 사용할 수 있습니다.

즉, 특정 노드의 자식노드들이 절대 W에 도달할 수 없을 경우 Pruning(가지치기)을 통해 탐색하지 않습니다.

따라서 탐색하는 노드의 수를 줄여 시간 복잡도도 줄일 수 있습니다.

Pruning Strategies 1

만약 탐색 전 우리가 weight들을 오름차순으로 정렬한다면, 다음 탐색해 볼 level의 weight는 가장 최근 탐색한 wight보다 클 것입니다.

그렇다면 현재까지 탐색한 노드들의 총 weight의 합이 이미 구하려는 값 W보다 크다면 나머지 노드들은 탐색할 필요가 없습니다.

즉, weight + w[i+1] > W 라면 Pruning(가지치기) 할 수 있습니다.

Pruning Strategies 2

만약 현재까지 탐색한 노드들의 weight들을 제외한 남은 weight들을 모두 더했을 경우 W보다 작다면 남은 값들을 계산해도 W에 도달할 가능성은 없습니다.

즉, weight + total < W 라면 Pruning(가지치기) 할 수 있습니다.

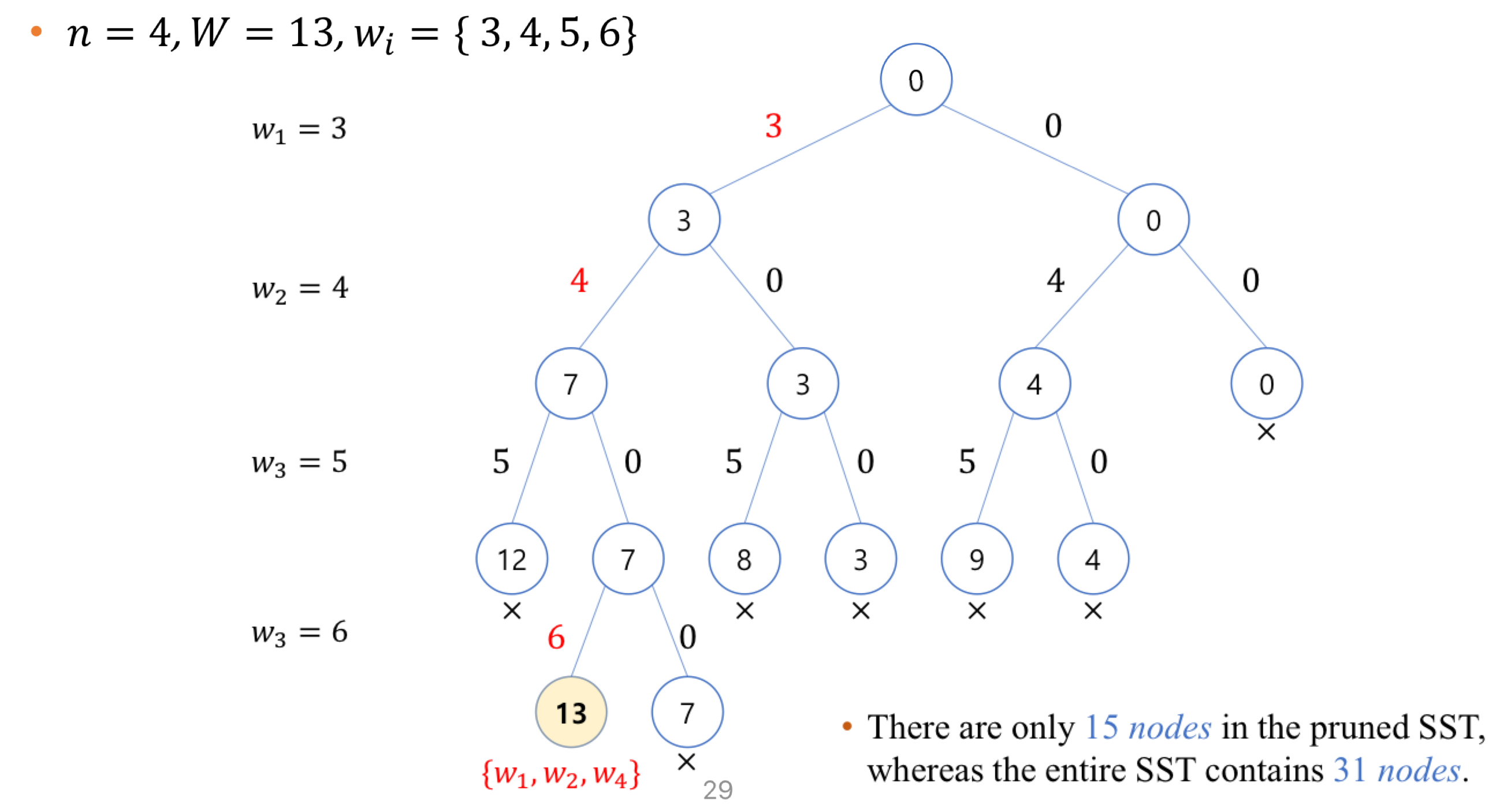
위와 같은 방식을 사용한다면 31개의 노드를 탐색하던 완전 탐색과는 달리 15개의 노드 만을 탐색하여 구현할 수 있습니다.

구현

i는 SST의 level, weight는 현재까지의 원소들의 총합, total은 남은 원소들의 총합 입니다.

먼저 생각 2에서 고민해보았던 pruning 전략들을 위해 promising()을 구현하였습니다.

def promising(i, weight, total):
    return (weight + total >= W) and (weight == W or weight + w[i + 1] <= W)

promising()을 통과하기 위해서는

• weight(현재까지의 부분집합 총합) + total(남은 원소들의 총합)이 W보다 크거나 같아야 하고
• weight(현재까지의 부분집합 총합) + w[i + 1](다음 노드의 값)이 W보다 작거나 같아야 합니다.

따라서 SST를 DFS로 탐색하되 promising()으로 불필요한 탐색을 없애주면 다음과 같습니다.

def sumOfSubsets(i, weight, total):
    global count
    if promising(i, weight, total):
        if weight == W: # solution
            count += 1
            subset = []
            for k in range(1, n + 1):
                if include[k] == True:
                    subset.append(w[k])
            solutionSubset.append(subset)
        else: # 다음 노드로
            include[i + 1] = True # w[i + 1]을 포함할 경우
            sumOfSubsets(i + 1, weight + w[i + 1], total - w[i + 1])
            include[i + 1] = False # w[i + 1]을 포함하지 않을 경우
            sumOfSubsets(i + 1, weight, total - w[i + 1])

def promising(i, weight, total):
    return (weight + total >= W) and (weight == W or weight + w[i + 1] <= W)

#input
n, W = map(int, input().split())
w = list(map(int, input().split()))
include = [False for _ in range(n + 1)]

w.insert(0, 0)

weight = 0 # 현재 무게
total = sum(w) # 남은 무게

count = 0
solutionSubset = []

sumOfSubsets(0,weight, total)

#output
print(count)
for i in range(0, count):
    print(" ".join(map(str, solutionSubset[i])))

해당 문제의 upper bound의 시간복잡도는 O(2^n)이였지만 BackTracking방식으로 시간을 줄일 수 있었습니다.

하지만, 해당 문제는 다항 시간 내에 풀 수 있다는게 증명되지 않은 NP-Complete problems입니다.