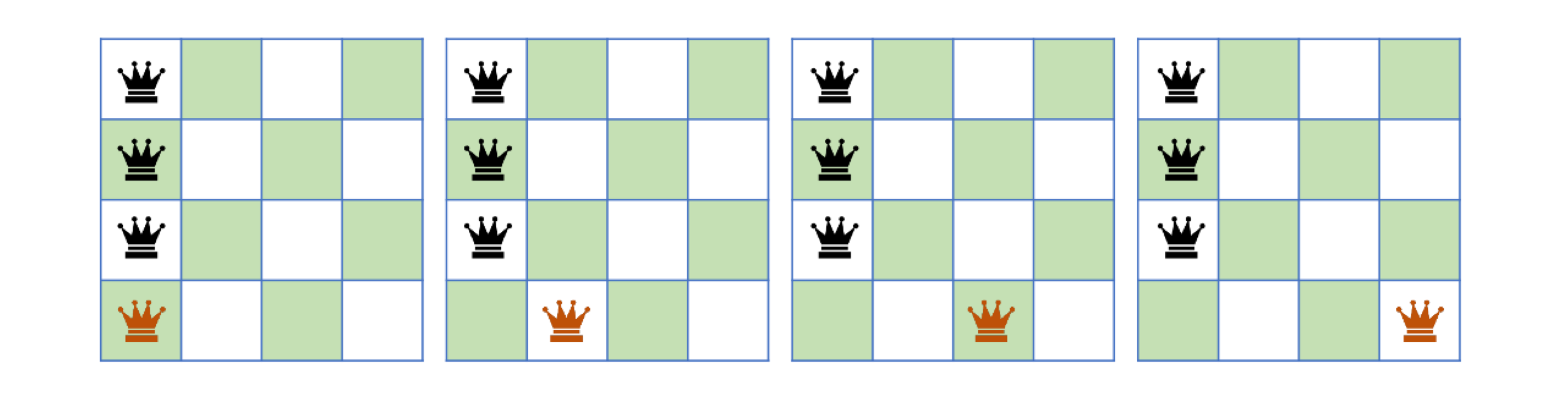
n-Queens Problem

n * n 의 체스 보드 판에 각 row마다 1개의 Queens를 놓는 문제입니다.
Queens를 놓을 때 criterion(제한조건)이 존재하는데 ..

creterion
1. same row
2. same column
3. same diagonal

위의 조건의 경우 서로의 여왕 말이 서로를 위협할 수 있기 때문에 배치가 불가능합니다.

---

생각 1.

해당 문제는 당연히 Brute-Force하게 해결할 수 있습니다.
먼저, n = 4라고 가정하고
State Space Tree(상태 공간 트리)를 생각해본다면

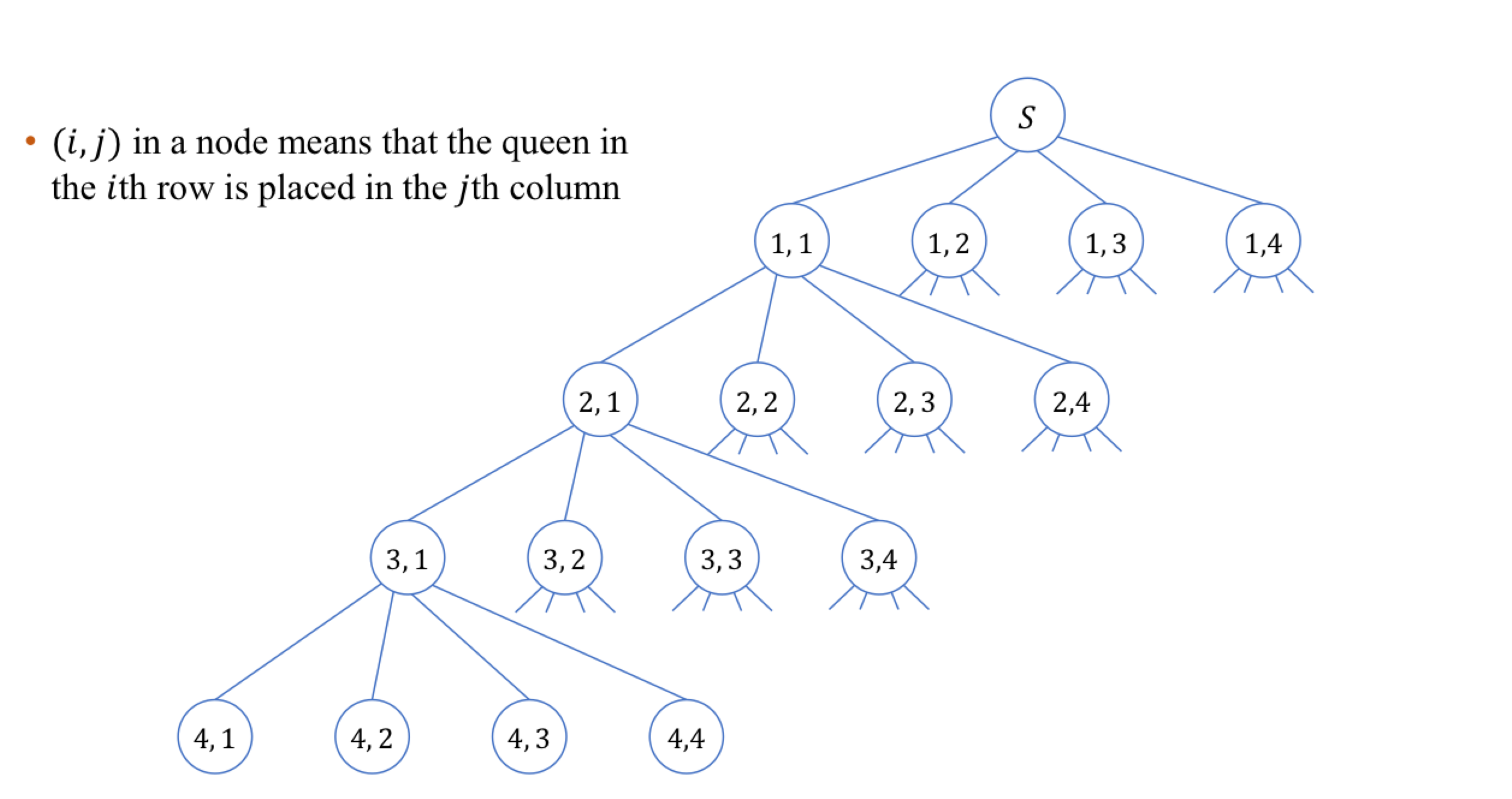
다음과 같이 그려 볼 수 있습니다.
row에 따라 해당하는 모든 column의 경우를 판단하고
이를 DFS(depth-first-search)의 방식으로 모든 경우의 수를 판단하면
결론적으로 배치할 수 있는 모든 Queens의 경우를 알 수 있습니다.

---

생각 2.

하지만 이러한 방식이 효율적이라 생각되지는 않습니다.
무려 n^4의 경우를 판단해야 하기 때문입니다.
즉, factorial time의 시간 복잡도가 소요됩니다.
따라서,
시작부터 해당 criterion에 걸리는 경우들을 Pruning(가지치기) 해버리는
Backtracking의 방식을 사용하여 더 효율적인 알고리즘을 생각 할 수 있습니다.

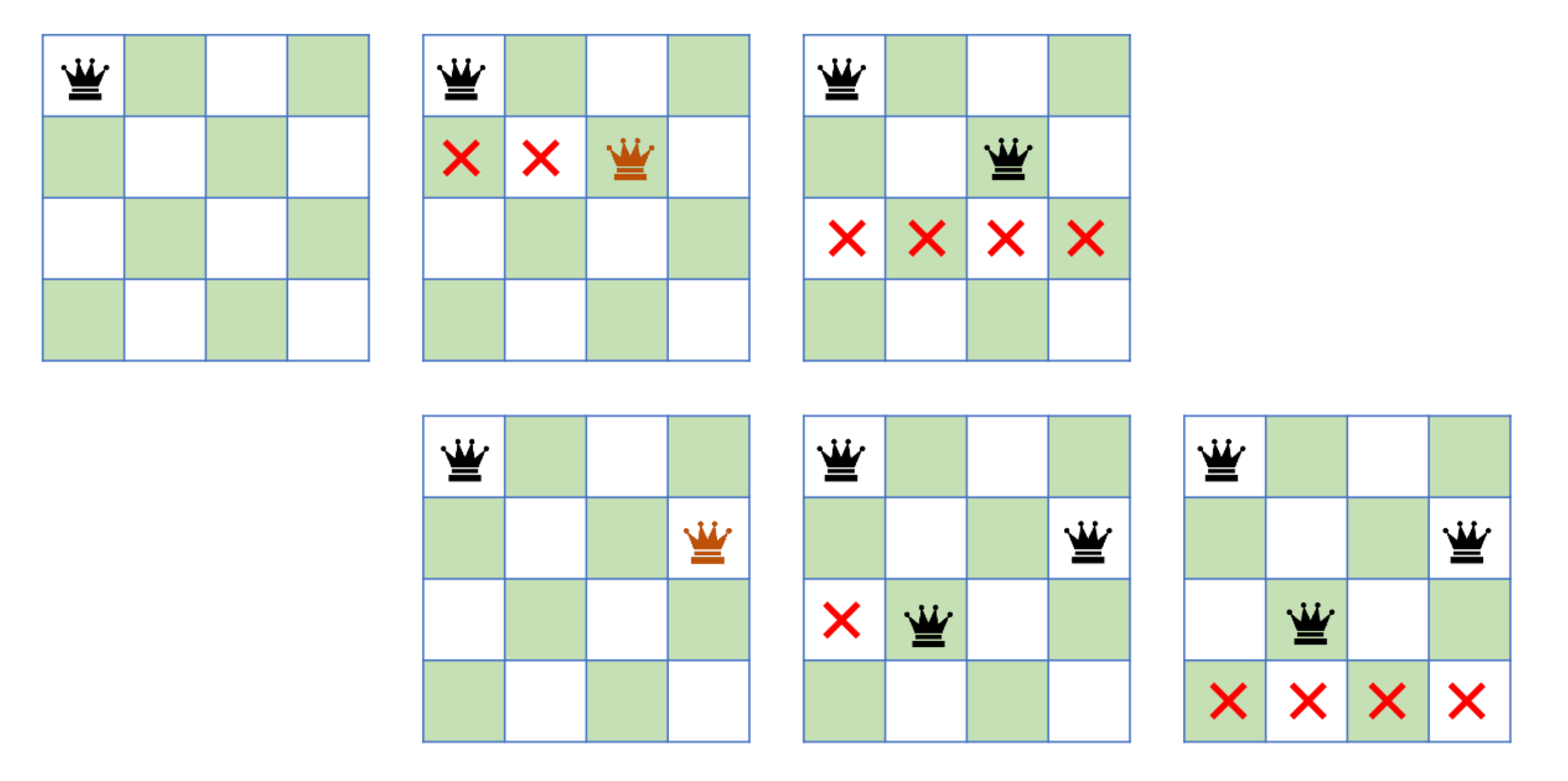
위 그림과 같이,
애초에 불가능 할 경우에는 다음 row의 경우를 생각하지 않고 탐색을 넘깁니다.

이를 State Space Tree를 그려보면 다음과 같습니다.

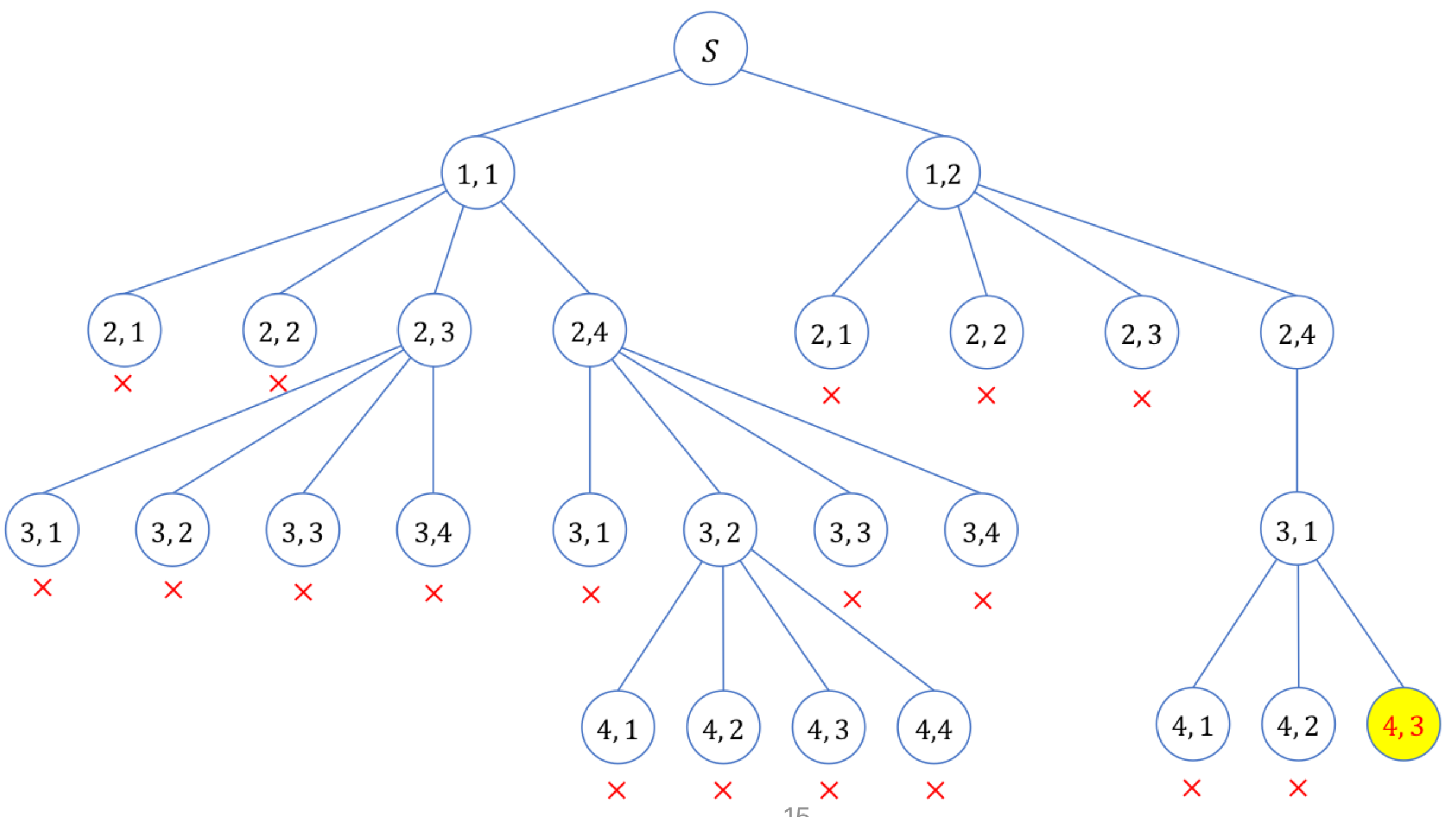
다음 코드는 놓을 수 있는 모든 n-Queens의 경우의 수와 해당하는 자리의 column 경우를 출력하도록 구현 해 보았습니다.

def nQueens(i, col):
    global count
    global max
    n = len(col) - 1
    if promising(i, col):
        if i == n: 
            count += 1   
            num = int(''.join(map(str, col[1:n + 1])))
            if max < num:
                max = num
            
        else:
            for j in range(1, n + 1): 
                col[i + 1] = j
                nQueens(i + 1, col)

def promising(i, col):
    k = 1
    flag = True
    while k < i and flag:
        if col[i] == col[k] or abs(col[i] - col[k]) == (i - k):
            flag = False 
        k += 1
    return flag

count = 0 
n = int(input())
col = [0] * (n + 1)
max = 0
nQueens(0, col)
print(count)
print(max)

먼저, Space State Tree와 같이 row 값은 따로 구현 할 필요가 없었습니다.
row가 1일 경우부터 차례대로 나아가면서 조건에 만족하는 column을 찾아가는 방식이니 당연하게 row는 위의 조건에 만족하게 될 것입니다.

따라서 row가 1일 경우 부터
차례로 column을 dfs(depth first search) 방식으로 탐색하되
경우에 따라 promising() 을 통해
criterion에 걸리게 되는 경우를 Pruning(가지치기) 하는 방식으로 구현하였습니다.

---

생각 3.

좀 더 생각을 해보니 위의 코드에서 더 효울적인 방식으로 코드를 작성할 수 있었습니다.
위의 코드는 nQueens()에 들어가서 해당 경우가 promising() 내 criterion 여부에 따라 계속해서 진행하거나 return되는 방식인데 굳이 nQueens()에서 판단하기보단,
먼저 후보가 되는 경우들을 promising() 을 통해 판단한 후 확실한 경우에만 nQueens()로 진입하는게 효율적이라 생각됩니다.

# 기존 방식대로 재귀를 거쳐서 promising을 할 시 효율성 낭비가 생긴다
# 따라서 먼저 promising을 통해 확인한 뒤 해당하는 노드만 다음 노드의 재귀문으로 들어간다.
def n_queens(i, cols): # i : 현재 row 
    global n, Max, count
    for col in range(1, n + 1): # 다음 row의 col 탐색 -> 먼저 확인하고 맞을 시 다음 재귀로 넘어간다.
        cols[i + 1] = col
        if promising(i + 1, cols): # 다음 row가 올바른지
            if i + 1 == n:
                result = int("".join(map(str, cols[1:n+1])))
                count += 1
                Max = max(Max, result)
            else:
                n_queens(i + 1, cols)
       
    

def promising(i, cols):
    k = 1
    flag = True
    # 지금까지의 col들과 모두 확인한다.
    while k < i and flag:
        if cols[k] == cols[i] or ((i - k) == abs(cols[i] - cols[k])): 
            flag = False
        k += 1
    return flag

n = int(input())
Max = 0
count = 0
cols = [0 for _ in range(n + 1)] # col 1 2 3 4 -> col 만 확인하면 되기 때문에
n_queens(0, cols)
print(str(count) + "\n" + str(Max))

위와 같이 구현 할 수 있습니다.

소감

Backtracking 을 공부하는 중 기초적인 문제이지만 개념을 확실하게 하지 않고 생각없이 무조건적으로 코드를 작성하는 습관이 들어있다보니 구현하는데 시간이 오래 걸렸습니다.

pseudo-code 에 대한 완전한 이해와 구현에 대한 생각을 완료하여 코드를 작성하는 것이 바람직하단 생각을 하게 되었습니다.