정의
- 퍼즐 게임의 일종으로 세 개의 기둥을 이용해서 원판을 다른 기둥으로 옮기면 된다.
- 제약 조건: 한번에 한개의 원판만 옮길수 있다. 큰 원판이 작은 원판 위에 있어서는 안된다.
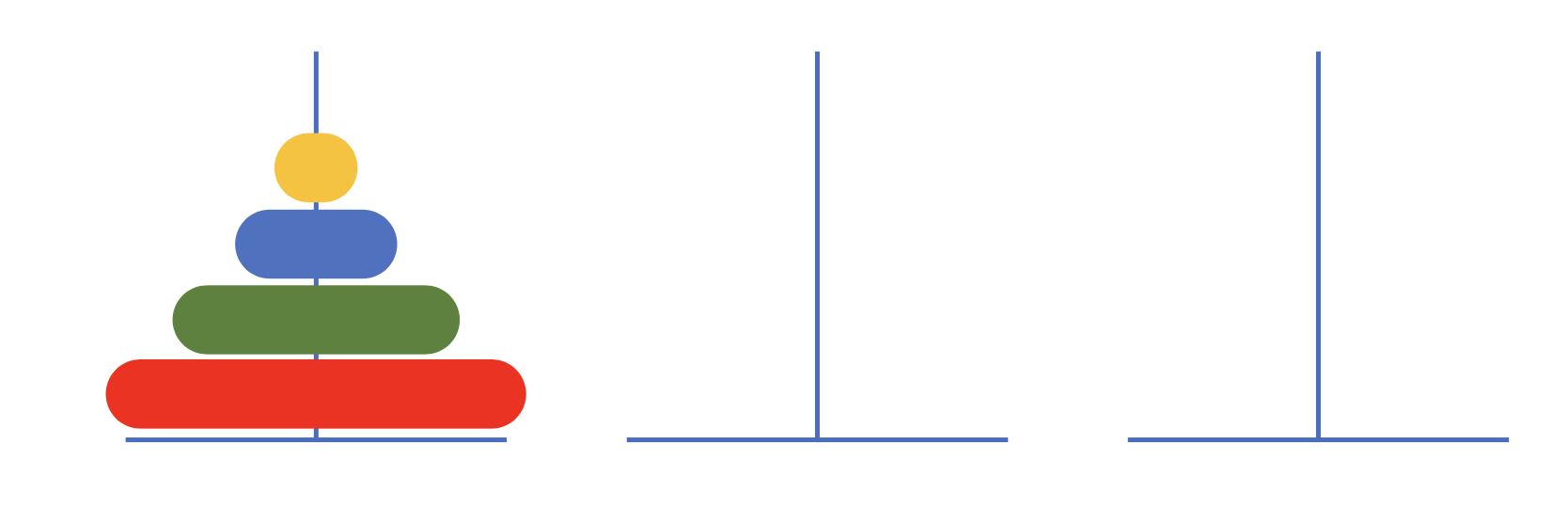
전설
고대 인도 베나레스에 있는 한 사원의 이야기 여기에는 다이아몬드로 이루어진 3개의 기둥이 있고, 그 기둥 중 하나에 가운데에 구멍이 나 기둥에 끼울 수 있게 된 64개의 크기가 각각 다른 황금 원반이 꽂혀 있다고 한다. 황금 원반은 가장 아래쪽에 있는 것이 가장 크고 위로 갈수록 점차 작아져 전체적으로 원추형의 탑을 이루고 있는데, 원반은 한 번에 하나씩만 옮길 수 있으며 작은 원반 위에 그보다 더 큰 원반을 옮길 수 없다. 이 규칙으로 64개의 원반을 처음 놓여 있던 막대에서 다른 막대로 모두 옮기면 탑은 무너지고 세상의 종말이 온다고 한다.
이 규칙들을 이용하여 63(64)개의 원반을 다른 막대로 전부 옮기는 것은 간단해 보이지만 '작은 원반 위에 큰 원반을 올릴 수 없다' 는 규칙은 의외로 크게 작용하는데, 이를 지키면서 n개의 원반을 한쪽 기둥에서 다른 쪽으로 옮기는 데 걸리는 최소 횟수가 2ⁿ−1번이기 때문이다.
n+1번째 원반을 목표로 하는 비어있는 한 기둥으로 옮기려면, 우선 그 위의 1번부터 n번째까지의 원반을 목표로 하는 기둥 이외의 비어있는 기둥으로 옮겨야만 한다. 이 사실을 이용해서 다음과 같이 1번부터 n+1번째까지의 원반을 목표로 하는 기둥으로 옮기는 데 요구되는 원반이동 횟수를 계산할 수 있다.
63개의 원반을 완전히 옮기는 데 걸리는 횟수는 2⁶³-1, 자그마치 922경 3372조 368억 5477만 5807회에 달한다. 판을 한 번 옮기는 데 1초가 걸린다 해도 약 2922억 7천만 년이 걸리는데, 이는 우주의 나이인 130~135억년보다도 훨씬 길며 중소형 적색왜성의 예상 수명과 맞먹는 시간이다. 세계멸망이 오고도 남을 만큼 길다.
하지만 만약 막대를 하나 더 추가해서 네 개로 만든다면 최소 18,433번만 옮기면 되는데, 1초에 판을 1개 옮긴다 할 때 5시간 7분 13초면 된다. 여전히 오래 걸린다.
퍼즐
위의 이야기에서 따와 3개의 기둥에 적당한 개수의 원반을 쌓아 놓고 다른 쪽으로 옮기는 게임.
원반 개수가 늘어날수록 이동 횟수가 엄청나게 늘어나기 때문에 많아야 7, 8개 정도만 쓰며 소모 시간으로 승부를 짓는 것이 보통인데, 이 정도면 1초에 원반 하나를 옮긴다 가정할 때 2~4분 정도 걸린다.
프로그래밍 공부를 하는 사람들의 초반의 벽이 이것의 알고리즘을 구현하는 것. 보통 재귀함수에 대해 공부할 때 예제로 쓰기 좋아 한번쯤은 보고 넘어가는 문제이다.
# 원판 개수, 출발 기둥, 도착 기동, 경유 기둥
def moveDisc(discCnt, fromBar, toBar, viaBar):
if discCnt == 1:
print(f'{discCnt}disc를 {fromBar}에서 {toBar}(으)로 이동!')
else:
# (discCnt -1)개들을 경유 기둥으로 이동
moveDisc(discCnt-1, fromBar, viaBar, toBar)
# discCnt를 목적 기둥이도 이동
print(f'{discCnt}disc를 {fromBar}에서 {toBar}(으)로 이동!')
# (discCnt-1)개들을 도착 기둥으로 이동
moveDisc(discCnt-1, viaBar, toBar, fromBar)
moveDisc(3, 1, 3, 2)
