Numpy. section5 : ndarray의 원소별 연산과 브로드캐스팅. Lec21. ndim이 다를 때의 브로드캐스팅

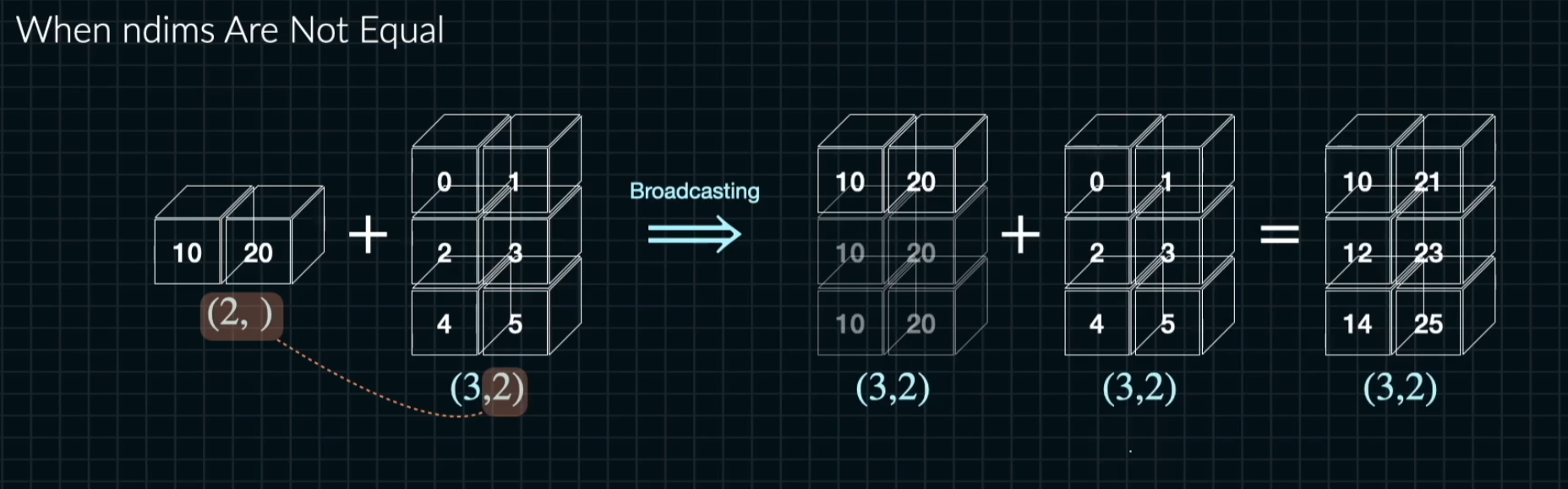
[1] When ndims Are Not Equal

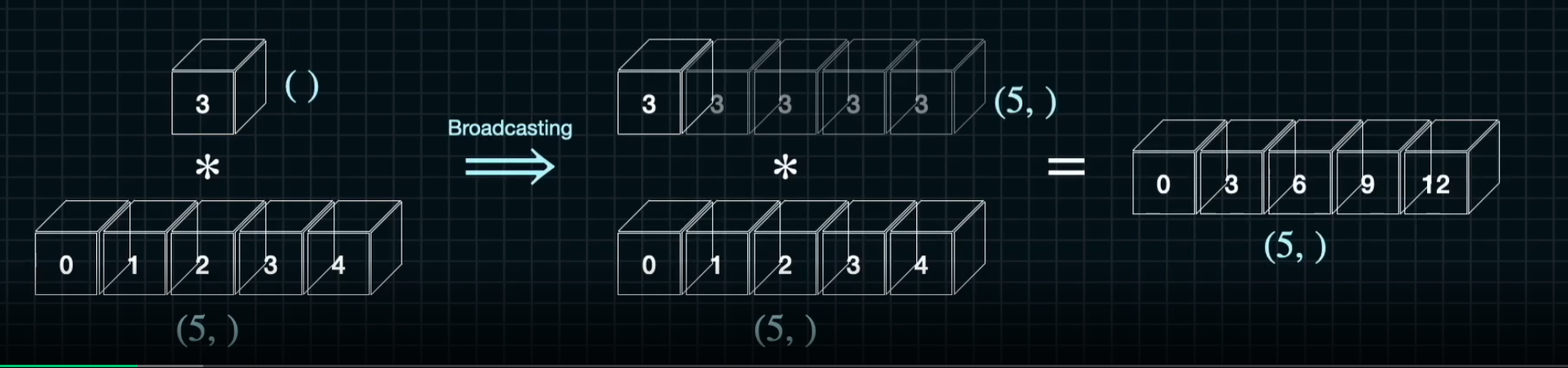
• 벡터와 스칼라가 연산될때에는 작은 차원이 브로드캐스팅됨

#1

A = np.array([10,20])
B = np.arange(6).reshape((3,2))
C = A + B

print("A: {}/{}\n{}".format(A.ndim, A.shape, A))
print("B: {}/{}\n{}\n".format(A.ndim, B.shape, B))

print("A + B: {}/{}\n{}".format(A.ndim, C.shape, C))

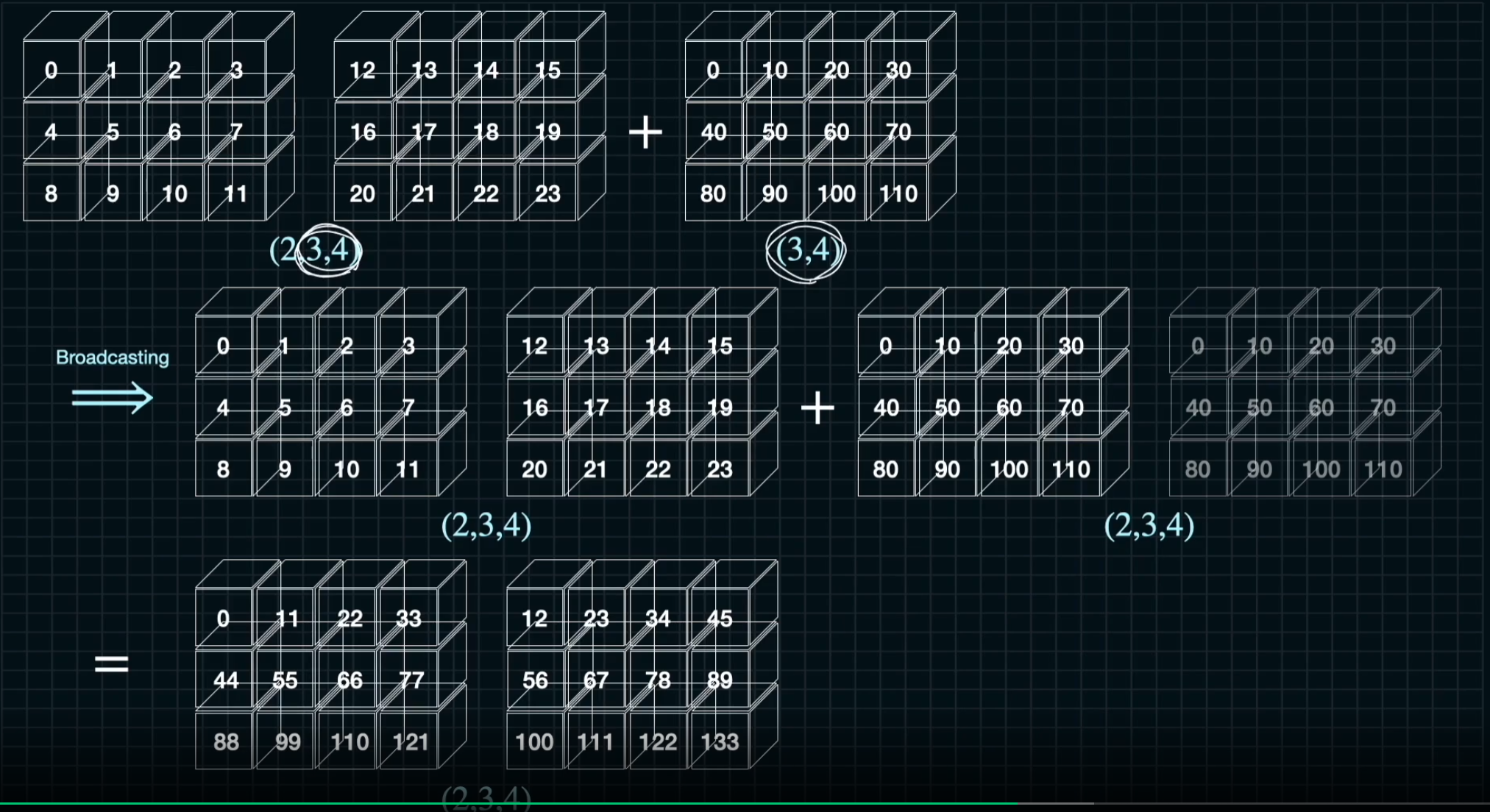
#2

A = np.arange(2*3*4).reshape((2,3,4))
B = 10 * np.arange(3*4).reshape((3,4))
C = A + B

print("A: {}/{}\n{}".format(A.ndim, A.shape, A))
print("B: {}/{}\n{}\n".format(A.ndim, B.shape, B))

print("A + B: {}/{}\n{}".format(A.ndim, C.shape, C))

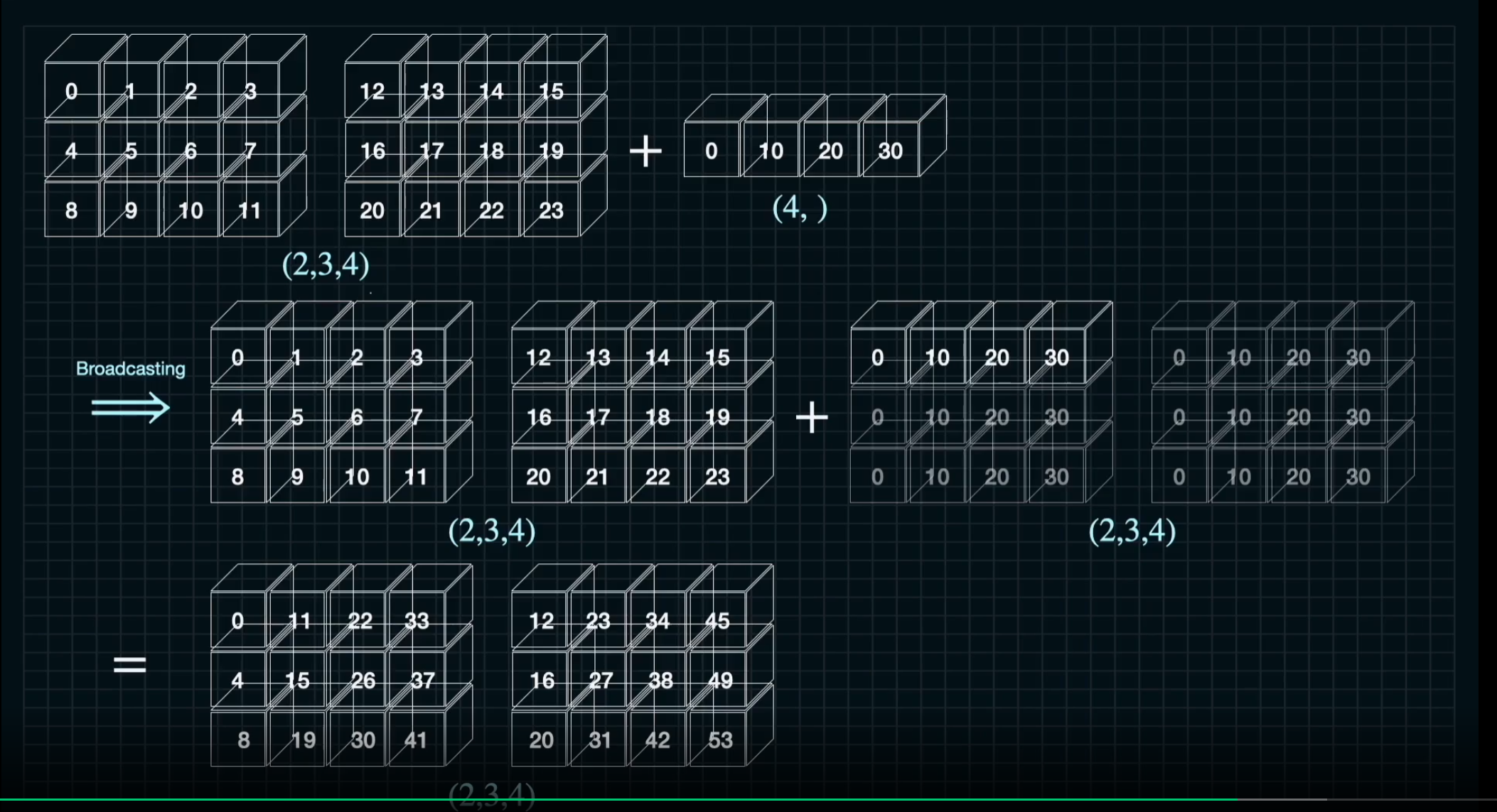
#3

A = np.arange(2*3*4).reshape((2,3,4))
B = 10 * np.arange(4)
C = A + B

print("A: {}/{}\n{}".format(A.ndim, A.shape, A))
print("B: {}/{}\n{}\n".format(A.ndim, B.shape, B))

print("A + B: {}/{}\n{}".format(A.ndim, C.shape, C))

• 오른쪽 정렬을 하면 브로드캐스팅 이해가 쉬워진다

[2] 전체코드

# When ndims Are Not Equal

import numpy as np

a = np.array(3)
u = np.arange(5)

print("shapes: {}/{}".format(a.shape, u.shape))
print("a: ", a)
print("u: ", u, '\n')

print("a+u: ", a+u)
print("a-u: ", a-u)
print("a*u: ", a*u)
print("a/u: ", a / u)
print("a // u: ", a // u)
print("a % u: ", a % u)
print("a ** u: ", a ** u, '\n')

print("a > u: ", a > u)
print("a >= u: ", a >= u)
print("a < u: ", a < u)
print("a <= u: ", a <= u)
print("a == u: ", a == u)
print("a != u: ", a != u)

#1

A = np.array([10,20])
B = np.arange(6).reshape((3,2))
C = A + B

print("A: {}/{}\n{}".format(A.ndim, A.shape, A))
print("B: {}/{}\n{}\n".format(A.ndim, B.shape, B))

print("A + B: {}/{}\n{}".format(A.ndim, C.shape, C))

#2

A = np.arange(2*3*4).reshape((2,3,4))
B = 10 * np.arange(3*4).reshape((3,4))
C = A + B

print("A: {}/{}\n{}".format(A.ndim, A.shape, A))
print("B: {}/{}\n{}\n".format(A.ndim, B.shape, B))

print("A + B: {}/{}\n{}".format(A.ndim, C.shape, C))

#3

A = np.arange(2*3*4).reshape((2,3,4))
B = 10 * np.arange(4)
C = A + B

print("A: {}/{}\n{}".format(A.ndim, A.shape, A))
print("B: {}/{}\n{}\n".format(A.ndim, B.shape, B))

print("A + B: {}/{}\n{}".format(A.ndim, C.shape, C))