[leetcode #105] Construct Binary Tree from Preorder and Inorder Traversal

Problem

Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.

Example 1:

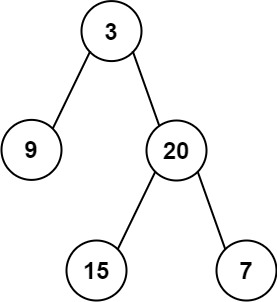
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

Example 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

Constraints:

· 1 <= preorder.length <= 3000
· inorder.length == preorder.length
· -3000 <= preorder[i], inorder[i] <= 3000
· preorder and inorder consist of unique values.
· Each value of inorder also appears in preorder.
· preorder is guaranteed to be the preorder traversal of the tree.
· inorder is guaranteed to be the inorder traversal of the tree.

Idea

Binary Tree의 preorder와 inorder가 주어졌을 때 Binary Tree를 만들어 리턴하는 문제다.

Tree와 관련된 대부분의 문제가 그렇듯이 이 문제 또한 재귀함수를 이용해 풀 수 있다.

재귀함수는 preorder를 구성하는 subarray의 index와 inorder를 구성하는 subarray의 index를 인자로 받는다.

preorder는 root부터 먼저 나오므로, preorder의 가장 첫 번째 원소를 값으로 하는 TreeNode를 만든다. inorder에서는 이 값을 기준으로 왼쪽에 있는 값들이 left subtree를 구성하는 노드가 되며, 오른쪽에 있는 값들이 right subtree를 구성하는 노드가 된다. inorder에서 root 값을 찾기 위해 inorder를 탐색하며 root index를 기준으로 preorder의 index와 inorder의 index를 각각 재귀함수에 다시 넣어주면 된다.

Time Complexity: O(n²)
Space Complexity: O(n)

root index를 inorder에서 매번 찾기보다 처음에 map을 구성해서 찾으면 Time Complexity를 O(n)으로 감소시킬 수 있다.

Solution

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int[] preorder;
    int[] inorder;

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        this.preorder = preorder;
        this.inorder = inorder;

        return traverse(0, preorder.length-1, 0, inorder.length-1);
    }

    private TreeNode traverse(int preStart, int preEnd, int inStart, int inEnd) {
        if (preStart > preEnd || inStart > inEnd) {
            return null;
        }
        TreeNode root = new TreeNode(preorder[preStart]);
        int rootIndex = rootInInorder(root.val, inStart, inEnd);
        int leftSize = rootIndex - inStart;
        root.left = traverse(preStart+1, preStart+leftSize, inStart, rootIndex-1);
        root.right = traverse(preStart+leftSize+1, preEnd, rootIndex+1, inEnd);

        return root;
    }

    private int rootInInorder(int val, int start, int end) {
        for (int i=start; i <= end; i++) {
            if (inorder[i] == val) {
                return i;
            }
        }

        return -1;
    }
}

Reference

https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/