[leetcode #221] Maximal Square

Problem

Given an m x n binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.

Example 1:

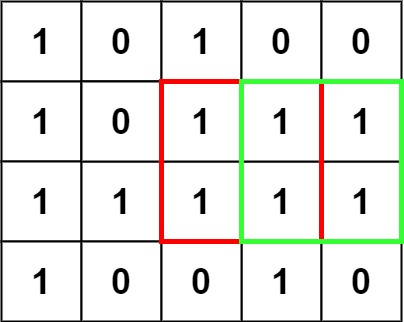
Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
Output: 4

Example 2:

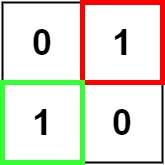
Input: matrix = [["0","1"],["1","0"]]
Output: 1

Example 3:

Input: matrix = [["0"]]
Output: 0

Constraints:

・ m == matrix.length
・ n == matrix[i].length
・ 1 <= m, n <= 300
・ matrix[i][j] is '0' or '1'.

Idea

값이 0 또는 1인 행렬이 주어질 때, 행렬 내에서 1로 이루어진 정사각형의 최대 넓이가 몇인지 구하는 문제다.
Brute Force로 풀어도 풀리는 문제지만, leetcode의 원칙과 맞지 않는 것 같아 dp를 통해 시간을 탄축하고 싶었다. (그래서 결국 못 풀고 답을 봤다.)
dp를 index (i,j)가 정사각형의 오른쪽 아래 꼭지점이라고 했을 때 정사각형의 최대값이라고 하면, 다른 dp 값은 다음과 같은 공식으로 구할 수 있다.

dp(i,j)=min(dp(i−1,j),dp(i−1,j−1),dp(i,j−1))+1.

dp가 위와 같은 공식이 되는 이유는 아래 그림을 보면 금방 이해가 된다. 왼쪽과 위쪽, 그리고 좌상 방향쪽의 dp값이 2일 때 현재 index에서 만들 수 있는 정사각형의 크기가 3이 된다. 이는 정사각형의 길이가 3일 때 1이 전부 차 있을 경우가 왼쪽과 위쪽, 좌상 방향쪽의 dp값이 2일 때기 때문이다.

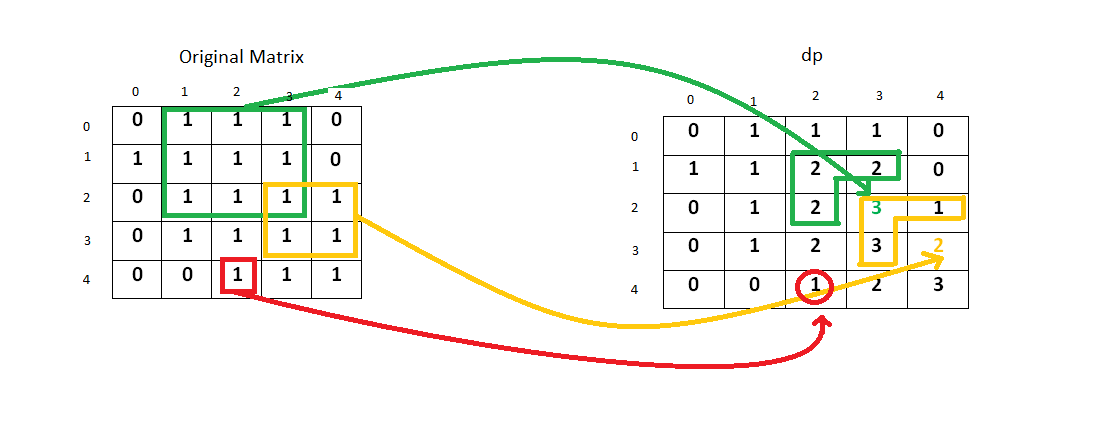
위와 같은 dp값을 구하고 나면 구현하는 건 쉽다. dp의 첫 행과 열은 모두 1로 비워둔 상태로 주어진 배열이 1일 때 위 공식을 이용해 dp값을 계산하면 된다. 새로 계산한 dp값과 정사각형이 최대가 되는 길이를 비교하여 더 크다면 최대 길이를 바꿔준다.

최대 길이를 이용해 정사각형의 넓이를 계산해서 리턴하면 된다.

Solution

public class Solution {
    public int maximalSquare(char[][] matrix) {
        int rows = matrix.length, cols = rows > 0 ? matrix[0].length : 0;
        int[][] dp = new int[rows + 1][cols + 1];
        int maxsqlen = 0;
        for (int i = 1; i <= rows; i++) {
            for (int j = 1; j <= cols; j++) {
                if (matrix[i-1][j-1] == '1'){
                    dp[i][j] = Math.min(Math.min(dp[i][j - 1], dp[i - 1][j]), dp[i - 1][j - 1]) + 1;
                    maxsqlen = Math.max(maxsqlen, dp[i][j]);
                }
            }
        }
        return maxsqlen * maxsqlen;
    }
}

Reference

https://leetcode.com/problems/maximal-square/