Problem
A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.
Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h)) are called minimum height trees (MHTs).
Return a list of all MHTs' root labels. You can return the answer in any order.
The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.
Example 1:
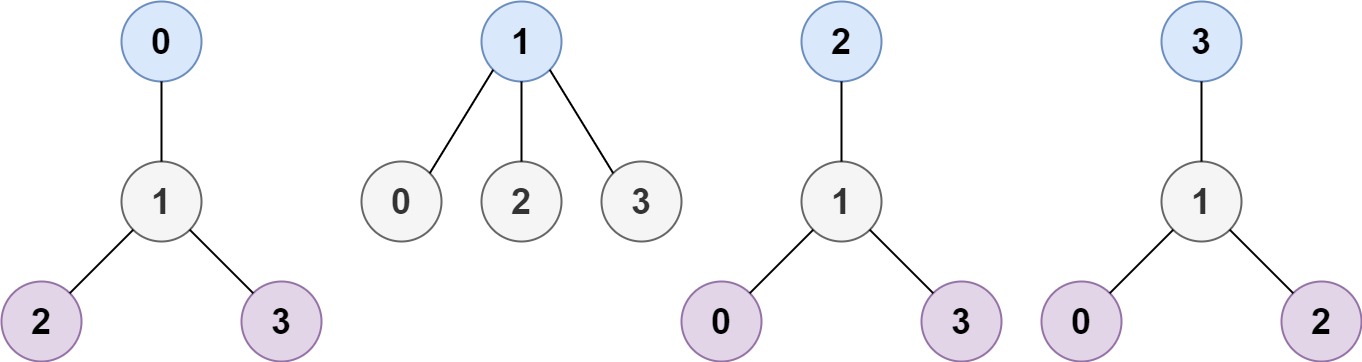
Input: n = 4, edges = [[1,0],[1,2],[1,3]] Output: [1] Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.Example 2:
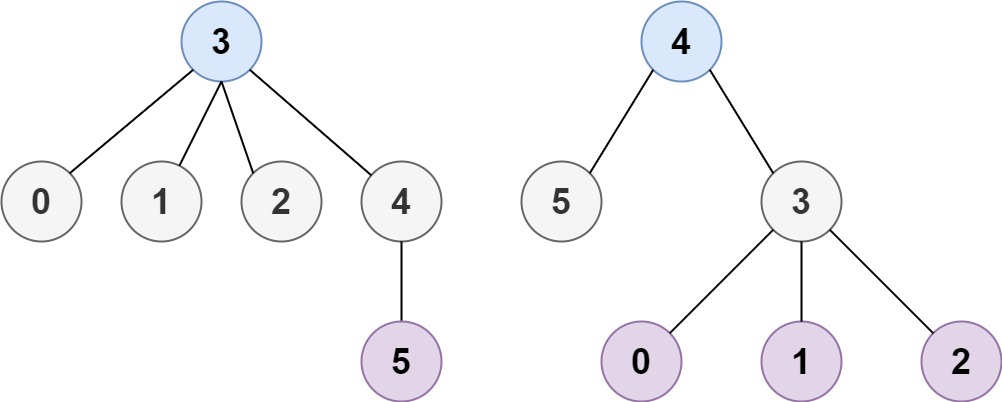
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]] Output: [3,4]Example 3:
Input: n = 1, edges = [] Output: [0]Example 4:
Input: n = 2, edges = [[0,1]] Output: [0,1]Constraints:
・ 1 <= n <= 2 * 10⁴ ・ edges.length == n - 1 ・ 0 <= aᵢ, bᵢ < n ・ aᵢ != bᵢ ・ All the pairs (aᵢ, bᵢ) are distinct. ・ The given input is guaranteed to be a tree and there will be no repeated edges.
Idea
Graph 관련된 문제라 그런지 많이 어려웠다 ㅠ 주어진 Graph에서 Tree의 높이가 최소가 되는 root node를 리턴하면 된다. 아래 Reference의 설명을 참조하면 centroids 노드가 최대 두 개가 가능한 이유가 설명되어 있다. 간단히 요약하면 Tree의 높이가 최소가 되는 노드가 세 개 이상이 되려면 Cycle이 생길 수밖에 없다는 것이다. 증명 과정이 유익하니 꼭 Solution을 읽어보는 걸 추천한다.
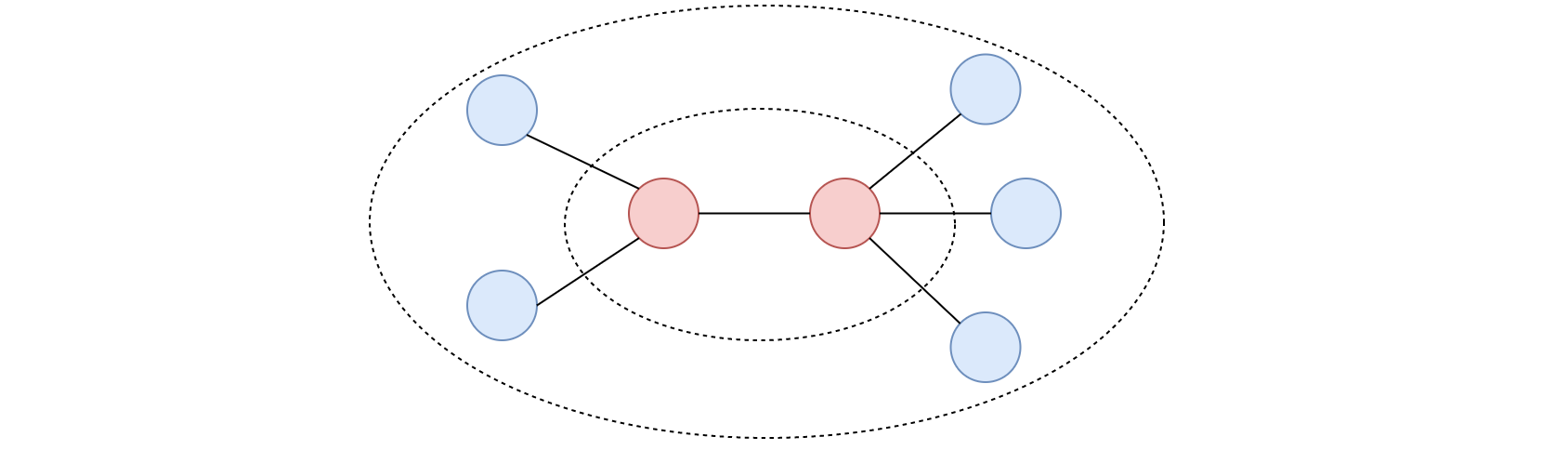
Centroid의 원리를 참조하면 leaf node를 제거하는 방식으로 Centroid만 남길 수 있다. 우선 처음에 edge를 탐색하면서 각 노드와 이웃한 노드들을 set으로 저장한다. leaf node인 경우 edge가 하나밖에 없으므로 leaf node를 따로 리스트로 저장할 수 있다.
이후엔 leaf node와 이웃한 노드에서 leaf node를 set에서 제거해 나간다. leaf node를 제거한 뒤에 해당 노드의 이웃 노드 크기가 1이라면 해당 노드 또한 leaf node가 되므로 leaf node 리스트에 저장한다.
새로운 leaf node 리스트가 생길 때마다 위 과정을 반복하고, 남은 노드가 2 이하가 되면 leaf node 제거를 멈춘다. 개수가 2개 이하가 되면 남은 노드들은 centroid가 되기 때문이다.
남은 centroid node들이 root node가 되었을 때 Tree의 높이가 최소인 node들이므로, centroid node들을 리턴하면 된다.
Solution
class Solution {
public List<Integer> findMinHeightTrees(int n, int[][] edges) {
// edge cases
if (n < 2) {
ArrayList<Integer> centroids = new ArrayList<>();
for (int i = 0; i < n; i++)
centroids.add(i);
return centroids;
}
// Build the graph with the adjacency list
ArrayList<Set<Integer>> neighbors = new ArrayList<>();
for (int i = 0; i < n; i++)
neighbors.add(new HashSet<Integer>());
for (int[] edge : edges) {
Integer start = edge[0], end = edge[1];
neighbors.get(start).add(end);
neighbors.get(end).add(start);
}
// Initialize the first layer of leaves
ArrayList<Integer> leaves = new ArrayList<>();
for (int i = 0; i < n; i++)
if (neighbors.get(i).size() == 1)
leaves.add(i);
// Trim the leaves until reaching the centroids
int remainingNodes = n;
while (remainingNodes > 2) {
remainingNodes -= leaves.size();
ArrayList<Integer> newLeaves = new ArrayList<>();
// remove the current leaves along with the edges
for (Integer leaf : leaves) {
// the only neighbor left for the leaf node
Integer neighbor = neighbors.get(leaf).iterator().next();
// remove the edge along with the leaf node
neighbors.get(neighbor).remove(leaf);
if (neighbors.get(neighbor).size() == 1)
newLeaves.add(neighbor);
}
// prepare for the next round
leaves = newLeaves;
}
// The remaining nodes are the centroids of the graph
return leaves;
}
}Reference
https://leetcode.com/problems/minimum-height-trees/
https://leetcode.com/problems/minimum-height-trees/solution/