[leetcode #441] Arranging Coins

Problem

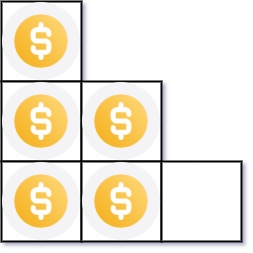
You have n coins and you want to build a staircase with these coins. The staircase consists of k rows where the ith row has exactly i coins. The last row of the staircase may be incomplete.

Given the integer n, return the number of complete rows of the staircase you will build.

Example 1:

Input: n = 5
Output: 2
Explanation: Because the 3rd row is incomplete, we return 2.

Example 2:

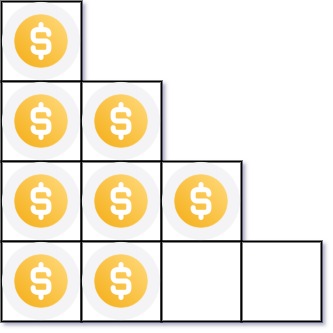
Input: n = 8
Output: 3
Explanation: Because the 4th row is incomplete, we return 3.

Constraints:

・ 1 <= n <= 2³¹ - 1

Idea

수학 지식을 이용해 푸는 문제다. n이 1씩 증가할 때 순열의 합 1 + 2 + ... + n = n * (n + 1) / 2다. Complete Rows의 수를 x라 할 때, n은 다음과 같은 식을 만족한다.

x(x + 1) / 2 ≦ n ﹤ (x + 1)(x + 2) / 2

x를 1씩 증가시키면서 주어진 수 n이 범위에 해당할 때 x를 리턴하는 방법도 있겠지만, Time Limit Exceeded에 걸린다. 따라서 주어진 식을 변형해서 다음과 같은 식을 만든다.

x(x + 1) ≦ 2n ﹤ (x + 1)(x + 2)

(x + 1)²이 항상 위 범위 내에 들어가므로 2n의 제곱근을 구한 뒤, 제곱근의 ±1 범위 내에 들어가는지 확인하기만 하면 된다. 범위 내에 해당하는 x값을 리턴하면 complete row의 개수가 나온다.

Solution

class Solution {
    public int arrangeCoins(int n) {
        long std = 2 * (long) n;
        long res = (long) Math.sqrt(std);

        if (std > res * (res - 1) && std < res * (res + 1))
            return (int) res - 1;

        if (std > (res -1) * (res - 2) && std < res * (res - 1))
            return (int) res - 2;

        return (int) res;
    }
}

Reference

https://leetcode.com/problems/arranging-coins/