[leetcode #96] Unique Binary Search Trees

Problem

Given an integer n, return the number of structurally unique BST's (binary search trees) which has exactly n nodes of unique values from 1 to n.

Example 1:

Input: n = 3
Output: 5

Example 2:

Input: n = 1
Output: 1

Constraints:

・ 1 <= n <= 19

Idea

node의 개수에 따라 BST의 가능한 형태가 어느 정도 되는지 세어보는 문제다.

BST라고 해서 반드시 tree를 만들 필요는 없다. 가능한 개수만 세면 되기 때문이다.

우선, 노드가 0개일 때와 1개일 때 가능한 수는 전부 하나다. 노드의 개수가 2개 이상인 경우를 생각해야 되는데, BST 특성 상 자식 노드는 최대 두 개를 가질 수 있다는 점을 떠올리면 된다. Root node를 제외한 노드의 개수는 n-1개이며, n-1개를 각각 왼쪽 자식 노드와 오른쪽 자식 노드에 분배를 한다고 가정하자. 그러면 n개보다 적은 노드일 때 계산한 결과값을 이용해서 n개의 노드일 때 가능한 BST의 수를 셀 수 있다.

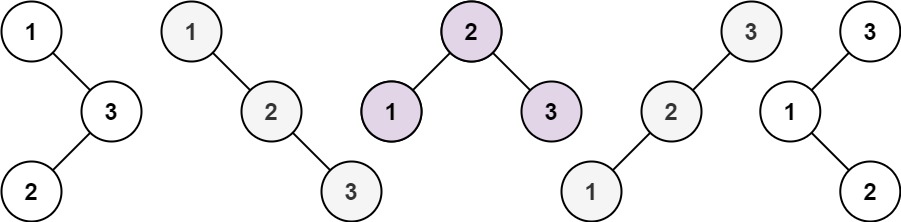
만약 노드의 개수가 5개라면, subtree의 노드 개수는 다음과 같은 형태가 가능하다.

(0,4), (1,3), (2,2), (3,1), (4,0)

그러면 노드의 개수가 5개인 BST 개수는 다음과 같다.

(BST 0) (BST 4) + (BST 1) (BST 3) + ... + (BST 4) * (BST 0)

매번 계산을 반복하지 않고 dp를 이용하면 0ms로 답을 구할 수 있다.

Solution

class Solution {
    int[] dp = new int[20];
    public int numTrees(int n) {
        for (int i=0; i <= n; i++) {
            numBST(i);    
        }

        return dp[n];
    }

    private void numBST(int n) {
        if (n == 0 || n == 1) {
            dp[n] = 1;
            return;
        }

        for (int i=0; i < n; i++) {
            dp[n] += dp[i] * dp[n-1-i];
        }
    }
}

Reference

https://leetcode.com/problems/unique-binary-search-trees/