[leetcode #546] Remove Boxes

Problem

You are given several boxes with different colors represented by different positive numbers.

You may experience several rounds to remove boxes until there is no box left. Each time you can choose some continuous boxes with the same color (i.e., composed of k boxes, k >= 1), remove them and get k * k points.

Return the maximum points you can get.

Example 1:

Input: boxes = [1,3,2,2,2,3,4,3,1]
Output: 23
Explanation:
[1, 3, 2, 2, 2, 3, 4, 3, 1] 
----> [1, 3, 3, 4, 3, 1] (3*3=9 points) 
----> [1, 3, 3, 3, 1] (1*1=1 points) 
----> [1, 1] (3*3=9 points) 
----> [] (2*2=4 points)

Example 2:

Input: boxes = [1,1,1]
Output: 9

Example 3:

Input: boxes = [1]
Output: 1

Constraints:

・ 1 <= boxes.length <= 100
・ 1 <= boxes[i] <= 100

Idea

문제의 원리는 연속된 색깔의 상자들이 나오면 상자들이 연속된 개수의 제곱만큼 값이 더해진다는 것이다. 박스들을 다 제거해 값을 구했을 때 어떤 경우에 최대값이 나오는지 확인하면 된다. 최대값을 구할 때 특정한 규칙이 있는 것이 아니므로 모든 경우를 다 계산해야 한다. 상자의 개수가 100개라고 brute force로 풀 수 있을 거라 생각하면 오산이다. 이 문제의 time complexity는 O(n!)이므로 최악의 경우 100!이라는 어마어마한 횟수만큼 시도해야 할 수도 있다.

중간 결과값을 dp로 저장하는 것이 필수인데, 이번 문제는 dp를 어떻게 정해야 할지 어려워 못 풀고 Solution을 참조했다. dp는 다음과 같이 정할 수 있다.

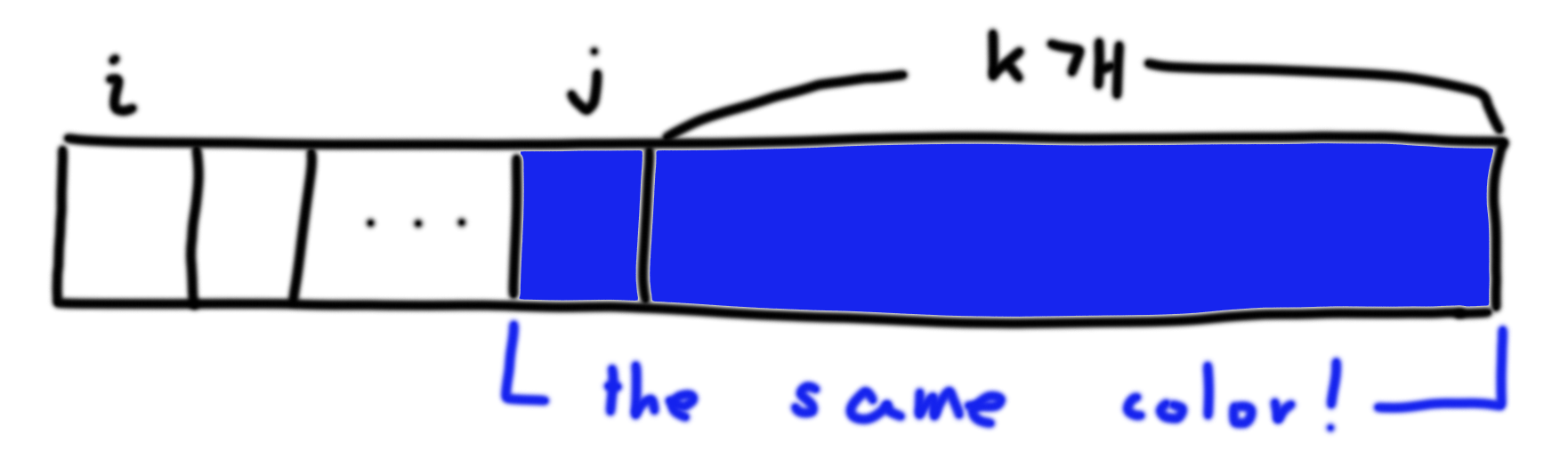
dp[i][j][k] → ith index에서 jth index까지 box가 있으며, box[j] 뒤로 boxes[j]값을 가진 box가 k개 있는 경우 최대값

2d array를 dp로 활용하는 건 익숙하지만, 3d array를 활용하는 것은 어렵다. 하지만 dp를 정하기만 할 수 있다면 문제를 푸는 건 식은 죽 먹기다. dp값을 구하기 위해 재귀함수를 활용하며, 재귀함수는 다음과 같다.

findMax(boxes, ith index, jth index, box[j] 뒤로 boxes[j]값을 가진 box의 개수)

알고리즘은 다음과 같다.

1. removeBoxes 함수에서 findMax 재귀함수를 findMax(boxes,0, len-1, 0)으로 호출한다.
2. findMax 함수
   a. ith index가 jth index보다 클 경우 0을 return한다.
   b. dp값이 설정되어 있을 경우 연산 없이 dp값을 return한다.
   c. ith index에서 (j-1)th index까지 box가 있으며 (j-1)번째 box와 같은 색을 가진 box가 뒤에 없을 경우의 최대값에 (k+1)*(k+1)을 더한 뒤 dp값으로 설정한다.
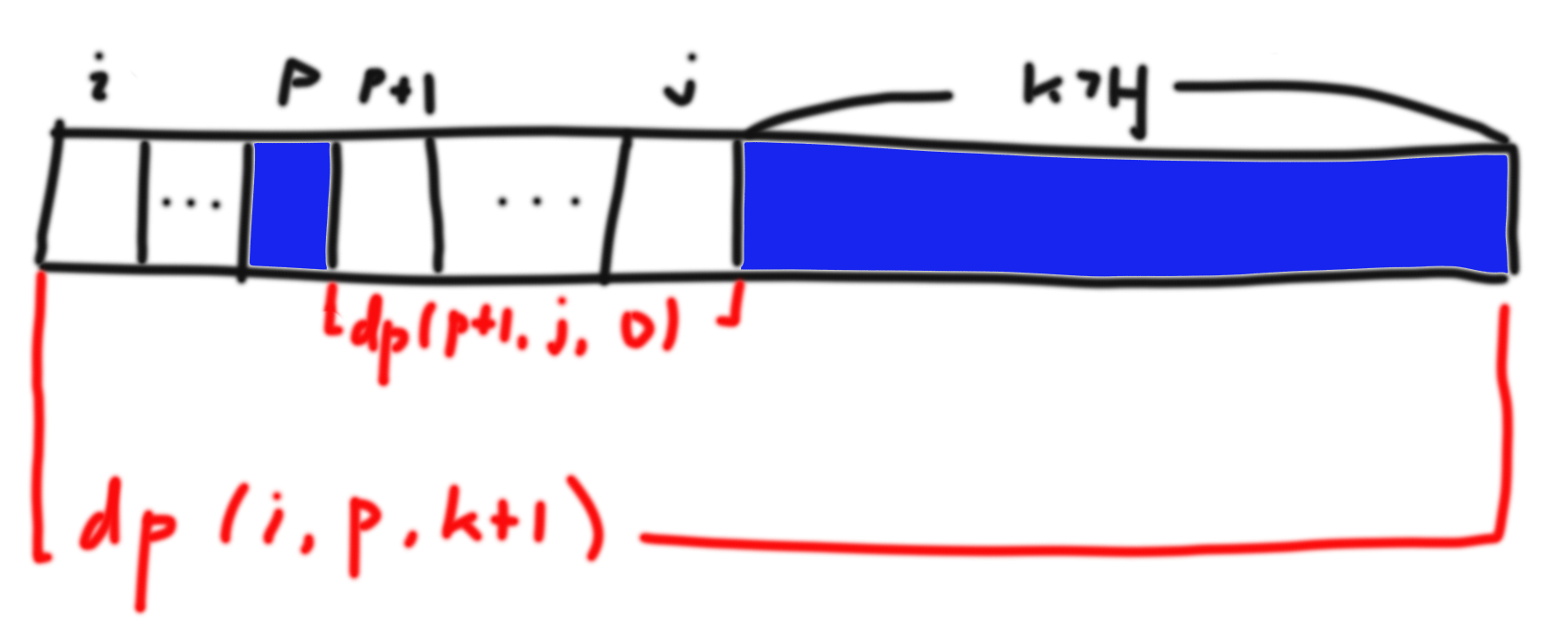
   d. box들 중 jth index에 해당하는 box와 색이 같은 것이 있는지 확인한다. 만약 있다면 (p+1)th index에서 (j-1)th index까지 box가 있으며 (j-1)번째 box와 같은 색을 가진 box가 뒤에 없을 경우의 최대값을 구한다. p번째 box와 j번째 box가 색이 같으므로 ith index에서 pth index가 있고 j번째 box를 포함한 (k+1)개의 box가 p번째 box 뒤에 있을 때 최대값을 구한다.
3. 계산된 dp값을 return한다. (i번째에서 j번째 box가 있으며, j번째 box와 같은 색의 box가 뒤에 없는 경우의 최대값)

Solution

class Solution {
    int[][][] dp;
    public int removeBoxes(int[] boxes) {
        int len = boxes.length;
        dp = new int[len][len][len];

        return findMax(boxes, 0, len-1, 0);
    }

    private int findMax(int[] boxes, int i, int j, int k) {
        if (i > j)
            return 0;
  
        if (dp[i][j][k] > 0)
            return dp[i][j][k];

        dp[i][j][k] = findMax(boxes, i, j-1, 0) + (k+1) * (k+1);

        for (int p=i; p < j; p++) {
            if (boxes[p] == boxes[j])
                dp[i][j][k] = Math.max(dp[i][j][k], (findMax(boxes, i, p, k+1) + findMax(boxes, p+1, j-1, 0)));
        }

        return dp[i][j][k];
    }
}

Reference

https://leetcode.com/problems/remove-boxes/
https://github.com/Seanforfun/Algorithm-and-Leetcode/blob/master/leetcode/546.%20Remove%20Boxes.md