[leetcode #76] Minimum Window Substring

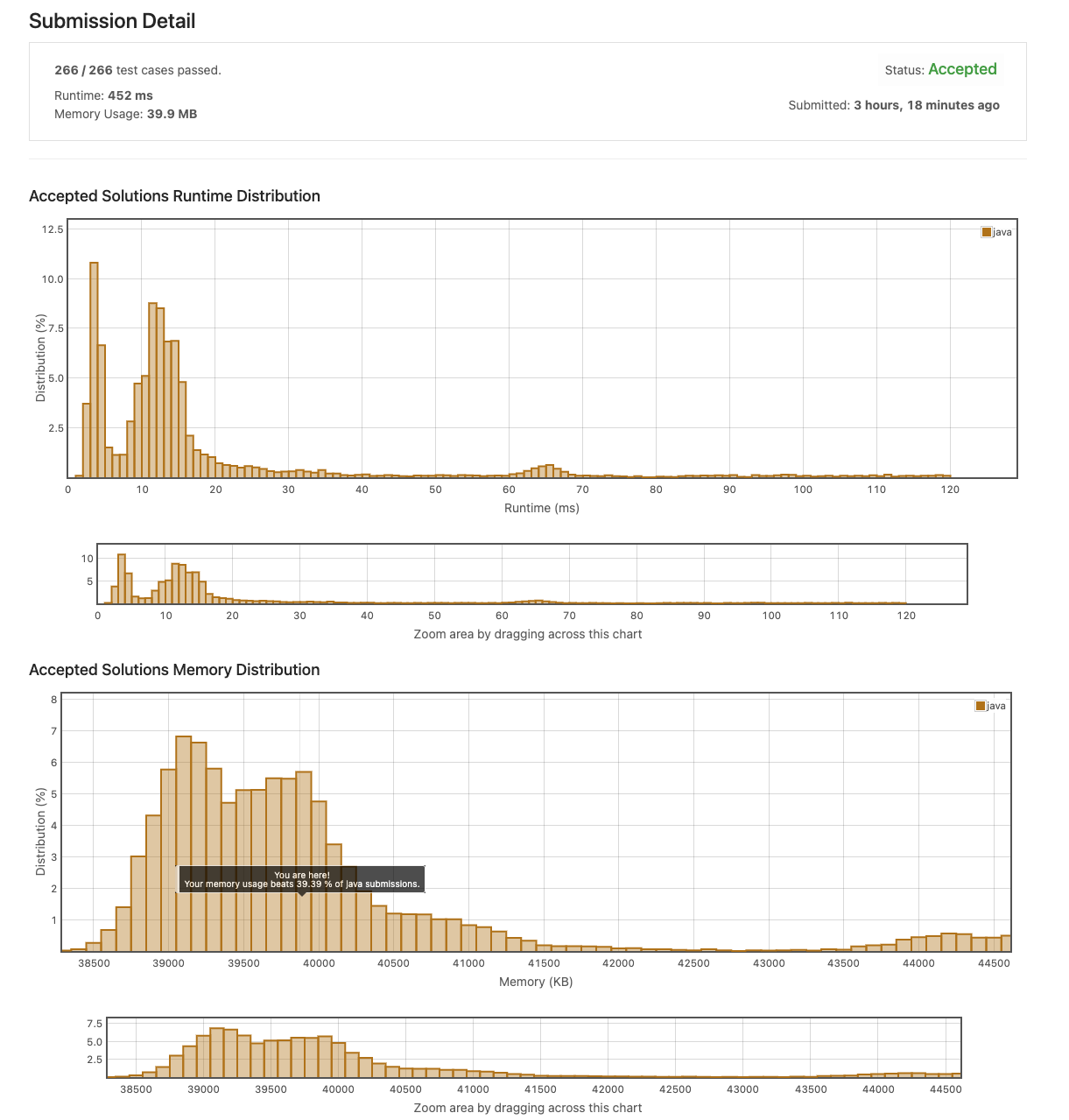
Problem

Given two strings s and t of lengths m and n respectively, return the minimum window substring of s such that every character in t (including duplicates) is included in the window. If there is no such substring, return the empty string "".

The testcases will be generated such that the answer is unique.

A substring is a contiguous sequence of characters within the string.

Example 1:

Input: s = "ADOBECODEBANC", t = "ABC"
Output: "BANC"
Explanation: The minimum window substring "BANC" includes 'A', 'B', and 'C' from string t.

Example 2:

Input: s = "a", t = "a"
Output: "a"
Explanation: The entire string s is the minimum window.

Example 3:

Input: s = "a", t = "aa"
Output: ""
Explanation: Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.

Constraints:

・ m == s.length
・ n == t.length
・ 1 <= m, n <= 105
・ s and t consist of uppercase and lowercase English letters.

Follow up: Could you find an algorithm that runs in O(m + n) time?

Idea

substring이 주제인 문제는 상당히 어려운 경우가 많다. Minimun Window Substring도 만만치 않은 문제다. t string에 들어있는 모든 문자가 포함된 s의 substring 중 가장 짧은 string의 길이는 얼마인지 구하는 문제다. 문제를 풀긴 했는데 너무 복잡하게 풀어서 다른 사람의 풀이를 봐야겠다는 생각이 든다.

풀이의 기본은 t string에 포함된 문자의 빈도수를 계산하고, s string을 탐색하면서 frequency를 이용해 t string의 모든 문자를 포함한 substring을 구하는 것이다. substring을 구한 뒤 이전에 구한 substring 길이의 최소값과 비교하면서 s string을 끝까지 탐색한다. 알고리즘은 다음과 같다.

1. t string의 빈도수를 문자별로 저장한다. 이 때 확인된 문자의 수도 저장한다.
2. s string을 탐색한다.
   a. t string에 포함되지 않은 문자라면 skip한다.
   b. 각 문자의 index를 저장하는 list를 사용한다. list의 크기는 계산한 빈도수이며, list가 꽉 찼을 경우 가장 앞의 index를 제거한다. 제거한 index가 substring의 첫번째 index라면, 첫번째 index를 다음 index로 바꿔준다.
   c. substring의 index는 prioiry queue로 관리한다. t string에 포함된 문자가 발견될 경우 해당 priority queue에 넣으며 각 문자의 index를 저장하는 list가 가득 찰 경우, 해당 list의 첫번째 index가 priority queue에서도 제거된다.
   d. 새로 발견된 substring의 길이를 측정하여 최소값과 비교한다. 최소값이 변경될 경우 substring의 첫번째 index와 마지막 index를 저장한다.
3. string s가 string t에 있는 모든 문자를 포함하지 않을 경우 빈 string을 리턴한다.
4. 저장한 index를 이용해 결과를 리턴한다.

Sliding Window라는 특성을 이용해 left pointer와 right pointer를 사용하는 방법이 훨씬 뛰어나다.

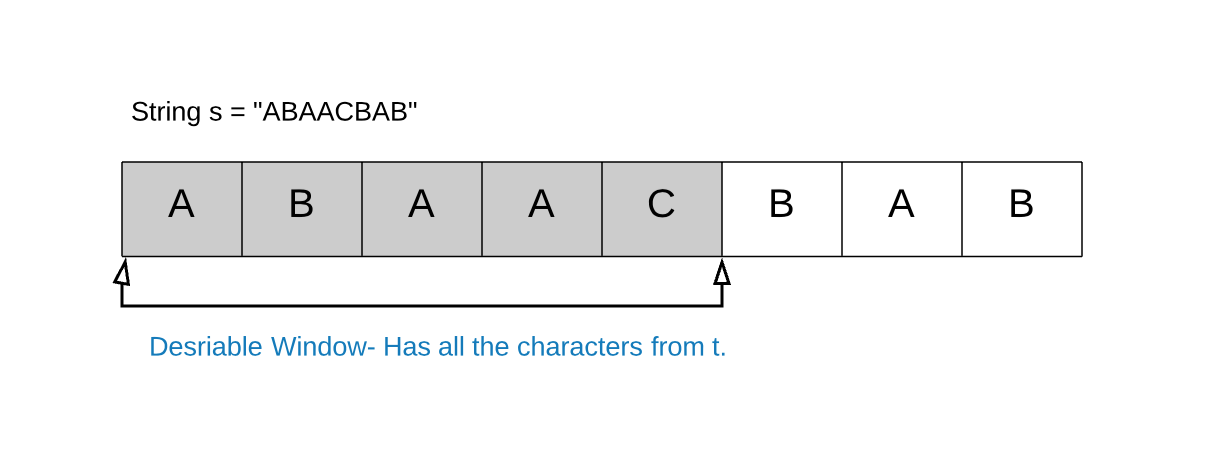
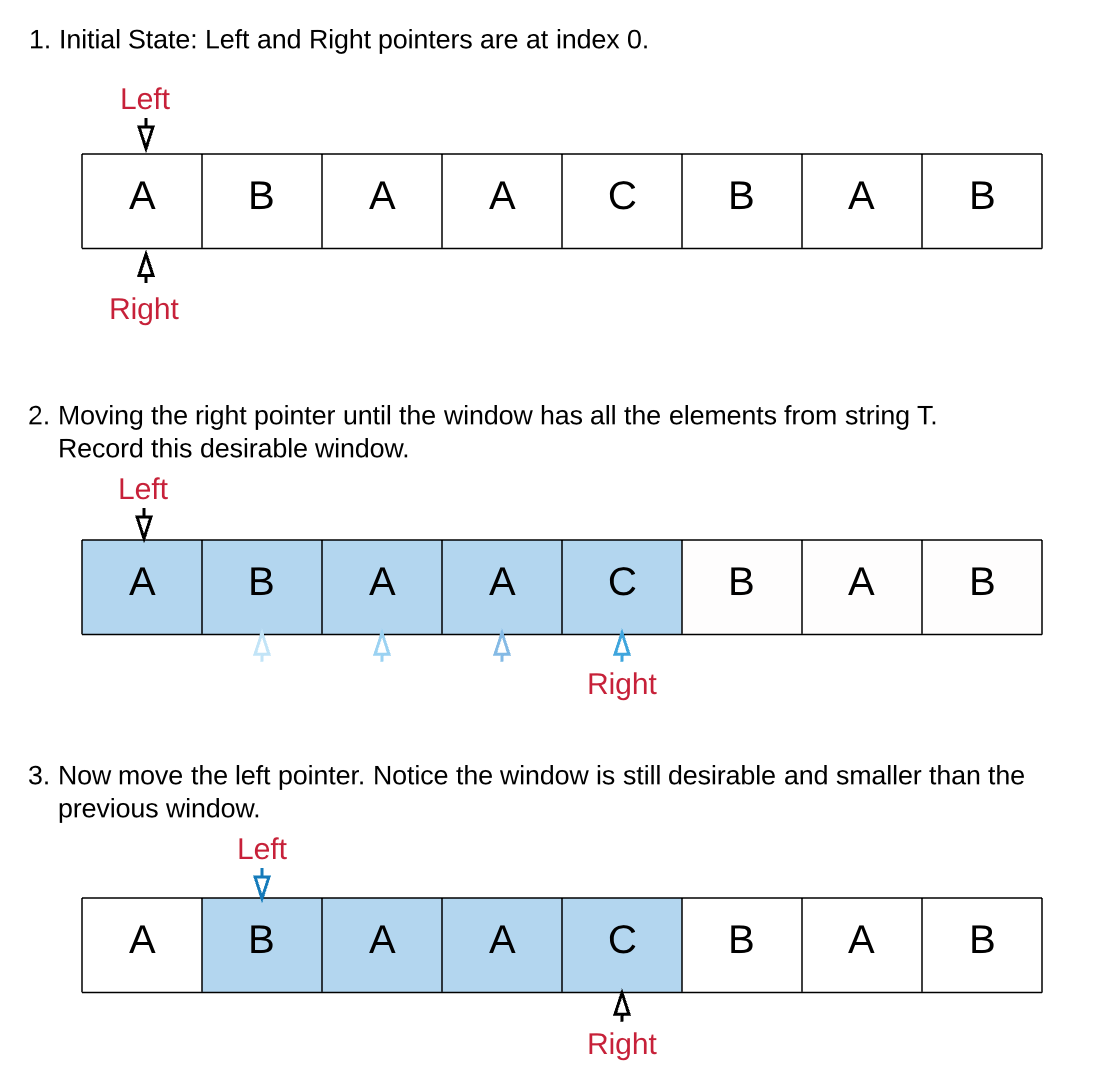
Solution

class Solution {
	public String minWindow(String s, String t) {
   	    // 1. Measure frequency of each characters in string t
	    int[] freqInT = new int[58];
	    int[] freqInS;
	    Arrays.fill(freqInT, -1);
        int charCnt = 0;
        for (char c : t.toCharArray()) {
            if (freqInT['z' - c] == -1) {
                charCnt++;
                freqInT['z' - c] = 0;
            }
            freqInT['z' - c]++;
        }
        freqInS = freqInT.clone();

        PriorityQueue<Integer> pq = new PriorityQueue<>();
        Map<Character, List<Integer>> indexes = new HashMap();
        for (char c='A'; c <='Z'; c++)
            indexes.put(c, new ArrayList());
        for (char c='a'; c <= 'z'; c++)
            indexes.put(c, new ArrayList());
  
        int min = 0;
	    int max = 0;
    	int len = Integer.MAX_VALUE;
        int minIndex = 0;
        int maxIndex = 0;

    	for (int i=0; i < s.length(); i++) {
            // 2. Confirm all characters in string t appear
            int frequency = freqInT['z' - s.charAt(i)];
            if (frequency < 0)
                continue;

            if (frequency > 0) {
                freqInS['z' - s.charAt(i)]--;
                if (freqInS['z' - s.charAt(i)] == 0)
                    charCnt--;
            }
   
            // 3. Determine minimum index of substring which contains all characters in string t
            List<Integer> indexList = indexes.get(s.charAt(i));
    	    int front = -1;
            if (indexList.size() >= freqInT['z' - s.charAt(i)]) {
                front = indexList.remove(0);
            }
            indexList.add(i);
            pq.add(i);
            min = pq.peek();
            if (front == min) {
                pq.poll();
                if (!pq.isEmpty())
                    min = pq.peek();
            } else {
                pq.remove(front);
            }

            // 4. change index and measure min length of substring
            max = i;
      
            if (charCnt != 0)
                continue;

            if (len > max - min) {
            	len = max - min;
                minIndex = min;
                maxIndex = max;
            }
	}
        if (charCnt != 0)
            return "";

        return s.substring(minIndex, maxIndex+1);
    }
}

결과는 최악...

leetcode에서 제안한 solution은 다음과 같다.

class Solution {
    public String minWindow(String s, String t) {

        if (s.length() == 0 || t.length() == 0) {
            return "";
        }

       // Dictionary which keeps a count of all the unique characters in t.
       Map<Character, Integer> dictT = new HashMap<Character, Integer>();
       for (int i = 0; i < t.length(); i++) {
          int count = dictT.getOrDefault(t.charAt(i), 0);
          dictT.put(t.charAt(i), count + 1);
       }

       // Number of unique characters in t, which need to be present in the desired window.
       int required = dictT.size();

       // Left and Right pointer
       int l = 0, r = 0;

       // formed is used to keep track of how many unique characters in t
       // are present in the current window in its desired frequency.
       // e.g. if t is "AABC" then the window must have two A's, one B and one C.
       // Thus formed would be = 3 when all these conditions are met.
       int formed = 0;

       // Dictionary which keeps a count of all the unique characters in the current window.
       Map<Character, Integer> windowCounts = new HashMap<Character, Integer>();

       // ans list of the form (window length, left, right)
       int[] ans = {-1, 0, 0};

       while (r < s.length()) {
           // Add one character from the right to the window
           char c = s.charAt(r);
           int count = windowCounts.getOrDefault(c, 0);
           windowCounts.put(c, count + 1);

           // If the frequency of the current character added equals to the
           // desired count in t then increment the formed count by 1.
           if (dictT.containsKey(c) && windowCounts.get(c).intValue() == dictT.get(c).intValue()) {
               formed++;
           }

           // Try and contract the window till the point where it ceases to be 'desirable'.
           while (l <= r && formed == required) {
               c = s.charAt(l);
               // Save the smallest window until now.
               if (ans[0] == -1 || r - l + 1 < ans[0]) {
                   ans[0] = r - l + 1;
                   ans[1] = l;
                   ans[2] = r;
               }

               // The character at the position pointed by the
               // `Left` pointer is no longer a part of the window.
               windowCounts.put(c, windowCounts.get(c) - 1);
               if (dictT.containsKey(c) && windowCounts.get(c).intValue() < dictT.get(c).intValue()) {
                   formed--;
               }

               // Move the left pointer ahead, this would help to look for a new window.
               l++;
           }

           // Keep expanding the window once we are done contracting.
           r++;   
       }

       return ans[0] == -1 ? "" : s.substring(ans[1], ans[2] + 1);
    }
}

Reference

https://leetcode.com/problems/minimum-window-substring/