백준 16639번 - 괄호 추가하기 3 / Python

https://www.acmicpc.net/problem/16639

문제

길이가 N인 수식이 있다. 수식은 0보다 크거나 같고, 9보다 작거나 같은 정수와 연산자(+, -, ×)로 이루어져 있다. 곱하기의 연산자 우선순위가 더하기와 빼기보다 높기 때문에, 곱하기를 먼저 계산 해야 한다. 수식을 계산할 때는 왼쪽에서부터 순서대로 계산해야 한다. 예를 들어, 3+8×7-9×2의 결과는 41이다.

수식에 괄호를 추가하면, 괄호 안에 들어있는 식은 먼저 계산해야 한다. 예를 들어, 3+8×7-9×2에 괄호를 (3+8)×7-(9×2)와 같이 추가했으면, 식의 결과는 59가 된다. 중첩된 괄호도 사용할 수 있고, 괄호 안에 여러 개의 연산자가 들어 있어도 된다. 즉, 3+((8×7)-9)×2, 3+((8×7)-(9×2)), (3+8)×(7-9×2) 모두 올바른 식이고, 결과는 97, 41, -121이다.

수식이 주어졌을 때, 괄호를 적절히 추가해 만들 수 있는 식의 결과의 최댓값을 구하는 프로그램을 작성하시오. 추가하는 괄호 개수의 제한은 없으며, 추가하지 않아도 된다.

입력

첫째 줄에 수식의 길이 N(1 ≤ N ≤ 19)가 주어진다. 둘째 줄에는 수식이 주어진다. 수식에 포함된 정수는 모두 0보다 크거나 같고, 9보다 작거나 같다. 문자열은 정수로 시작하고, 연산자와 정수가 번갈아가면서 나온다. 연산자는 +, -, 중 하나이다. 여기서 는 곱하기 연산을 나타내는 × 연산이다. 항상 올바른 수식만 주어지기 때문에, N은 홀수이다.

출력

첫째 줄에 괄호를 적절히 추가해서 얻을 수 있는 결과의 최댓값을 출력한다. 정답은 231보다 작고, -231보다 크다.

나의 풀이

• DP의 대표적인 문제 중 하나인 '최적의 행렬 곱셈 구하기'와 형태가 비슷하여 DP로 풀 수 있을 것이라 판단했다.
• DP는 크기는 다르고, 반복되는 구조의 문제를 중복 없이 효율적으로 푸는 방법이기에, 최적부분구조를 찾으려 노력했다.
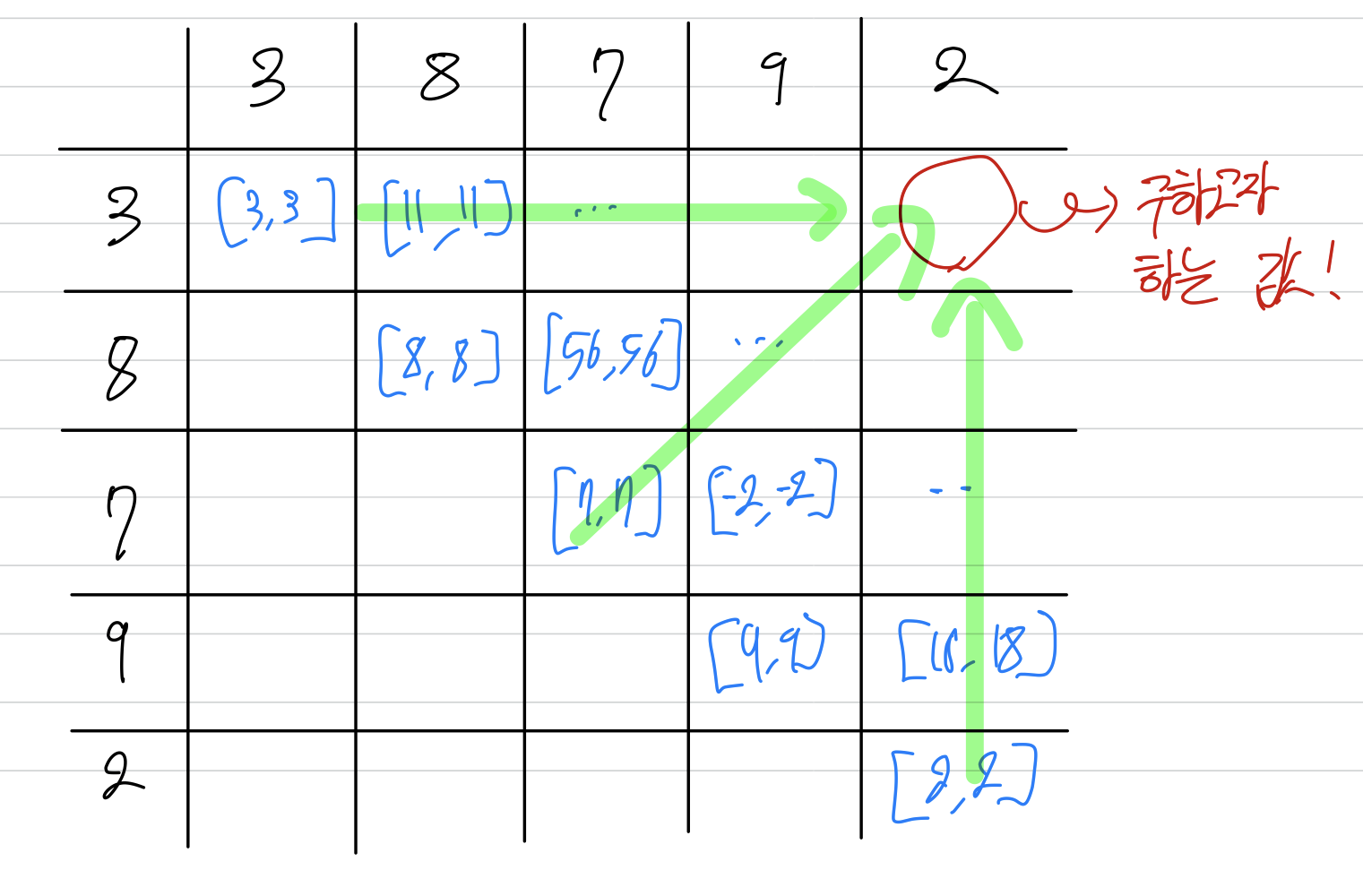
• 결과 아래와 같이 최적부분구조를 찾을 수 있었다.
  
• 하지만 첫번째 시도 후 실패했는데, 아래와 같은 반례를 찾는데 상당한 시간이 걸렸다.
  
• 결국 bottom-up방식으로 풀기 위해 리스트에 최댓값, 최솟값을 모두 계산, 저장하는 방식으로 수정했고 정답을 도출할 수 있었다.
  

코드

def getMaxMin(board, oper, i, j):
	"""
    입력
    board : bottom-up계산을 위한 리스트
    oper : 연산자가 담겨있는 리스트
    i, j : 인덱스
    출력
    -> i ~ j범위를 계산했을 때 최대, 최소 값을 반환한다.
    """
    tmp = []
    for mid in range(i, j):
        if oper[mid] == '+':
            tmp.append(board[i][mid][0] + board[mid+1][j][0])
            tmp.append(board[i][mid][0] + board[mid+1][j][1])
            tmp.append(board[i][mid][1] + board[mid+1][j][0])
            tmp.append(board[i][mid][1] + board[mid+1][j][1])
        elif oper[mid] == '-':
            tmp.append(board[i][mid][0] - board[mid+1][j][0])
            tmp.append(board[i][mid][0] - board[mid+1][j][1])
            tmp.append(board[i][mid][1] - board[mid+1][j][0])
            tmp.append(board[i][mid][1] - board[mid+1][j][1])
        else:
            tmp.append(board[i][mid][0] * board[mid+1][j][0])
            tmp.append(board[i][mid][0] * board[mid+1][j][1])
            tmp.append(board[i][mid][1] * board[mid+1][j][0])
            tmp.append(board[i][mid][1] * board[mid+1][j][1])
    return max(tmp), min(tmp)

# 수식 길이
N = int(input())

# 피연산자의 길이
n = N // 2

# 수식 입력
formula = input()

# 피연산자, 연산자 
num, oper = [], []
for idx, item in enumerate(formula):
    if idx % 2 == 0:
        num.append(int(item))
    else:
        oper.append(item)

# bottom-up방식으로 풀기 위해 리스트 생성, 
# 가장 안쪽의 [0, 0]은 각 각 최솟값, 최댓값을 저장
board = [[[0, 0] for i in range(n+1)] for j in range(n+1) ]

# scope -> 최댓값과 최솟값을 구하려는 범위
# 적은 범위부터 최댓값, 최솟값을 구해 가며 각 경우들을 저장한다.
for scope in range(n+1):
    for i in range(0, n-scope+1):
        j = i + scope
        if i == j:
            board[i][j][0] = num[i]
            board[i][j][1] = num[i]
        else:
            maxV, minV = getMaxMin(board, oper, i, j)
            board[i][j][0] = maxV
            board[i][j][1] = minV

print(max(board[0][n]))