👨‍🏫학습목표

오늘은 Target Network의 작동원리와 DQN의 pseudo code, DQN 속 CNN에 대해 배워볼 예정이다.

👨‍🎓강의영상: https://www.youtube.com/watch?v=C-mfKSM0VFQ&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=18

1️⃣ Target Network

📕 지난 시간에 배운 내용

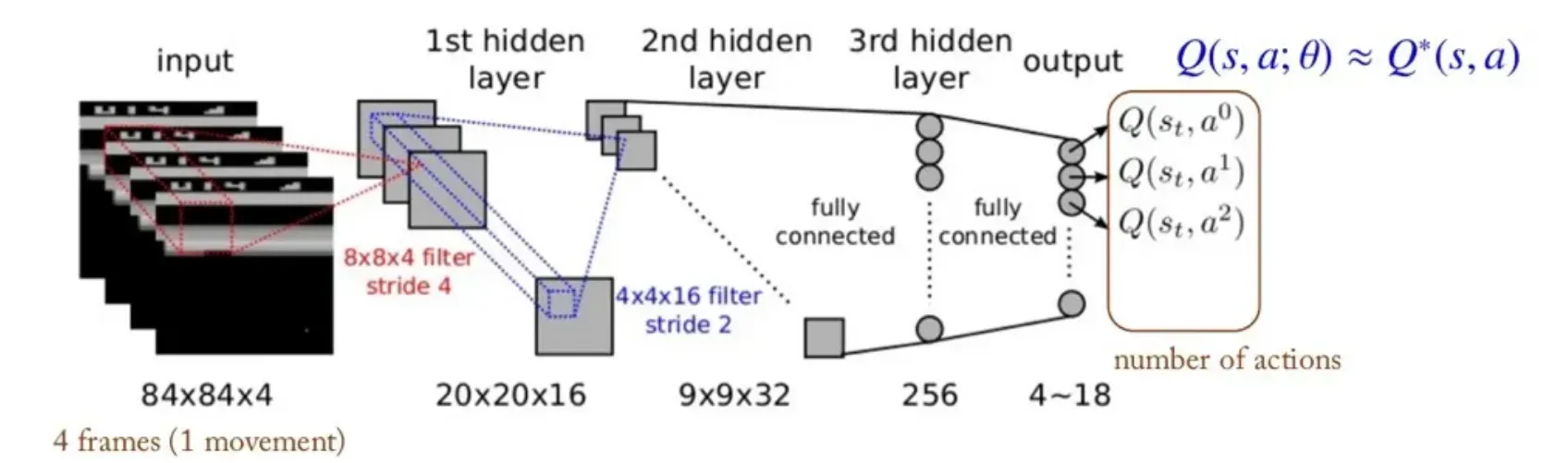
• DQN은 Q-learning에서 Q-table 대신 Q-Network를 사용하는 모델이다.
• DQN은 state space가 크거나 continuous해도 데이터를 처리할 수 있다.
• 다만 Action space는 아직 작고, discrete하다.
• DQN는 Replay Buffer와 Target Network를 통해 성능을 개선한다.

🔷 Target Network

🔻 Naïve DQN의 Loss function

$L(\theta) = [r_{t+1} + \gamma \max_a Q(s_{t+1}, a; \theta) - Q(s_t, a_t; \theta)]^2$

• Target으로 $Q(s_{t+1}, a; \theta)$를 사용하는데, 이 값은 업데이트할 때마다 다른 값을 가진다.
• 즉 하나의 minibatch 내에서 업데이트를 진행할 때, samp에 따라 Target값이 계속 바뀐다.
• 이를 Non-stationary target problem이라 한다.

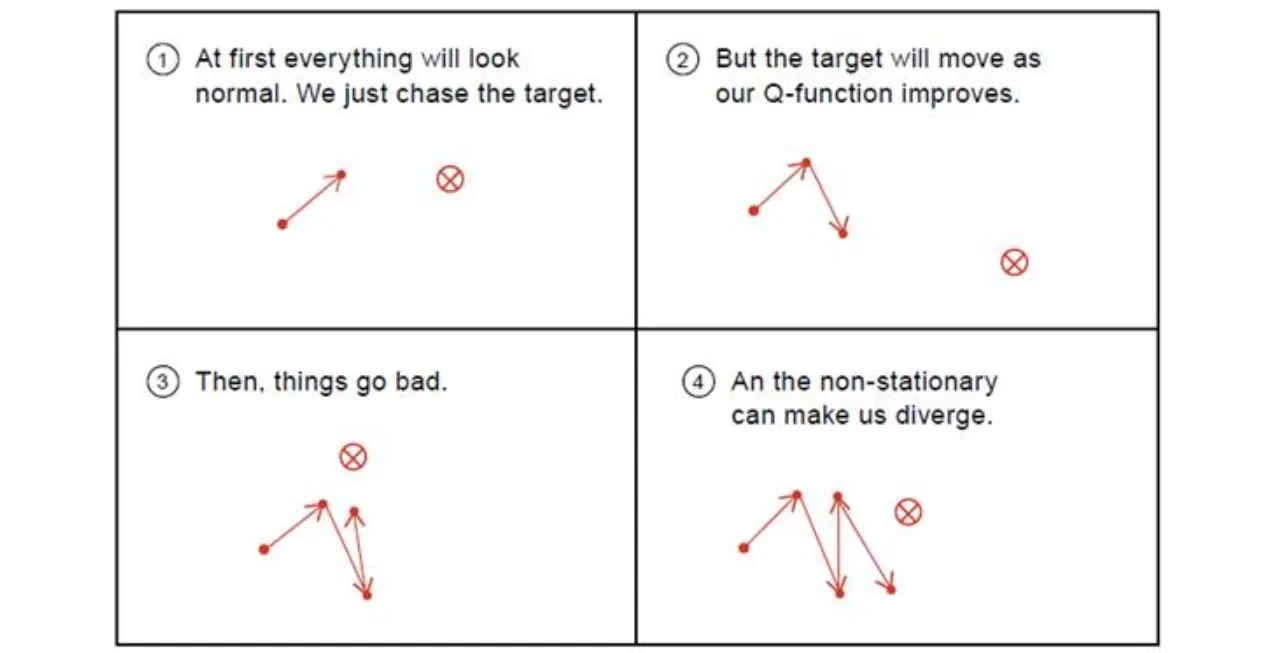
출처: https://livebook.manning.com/book/grokking-deep-reinforcement-learning/chapter-9/v-9#27

✨이러한 문제를 해결하기 위해서는 Target Network를 고정해야 한다.

🔻 Behavior $Q$-Network

• 모델이 실제로 행동할 때 사용하는 Network이다.
• $- \ Q(s_t, a_t; \theta)$ 에 해당한다.

🔻 Target $\hat{Q}$-Network

• $\max_a Q(s_{t+1}, a; \theta)$에 해당한다.

🔻 Target Network의 구현 방법

• Behavior $Q$-Network $\theta$는 매번 업데이트를 진행한다.
• Target $\hat{Q}$-Network $\hat{\theta}$은 업데이트 하지 않고 고정한다.
• Target $\hat{Q}$-Network $\hat{\theta}$은 일정 time step이 지난 후 $\theta$로 업데이트한다.
• 동일한 CNN Q-Network를 사용하지만 서로 다른 파라미터 $\theta,\ \hat{\theta}$ 을 사용하는 것이다.

🔷 Target Network의 Loss function

🔻 Forward pass

$L(\theta) = \frac{1}{|\mathcal{B}|} \sum_{i=|\mathcal{B}|} [r_{i+1} + \gamma \max_a \hat{Q}(s_{i+1}, a; \hat{\theta}) - Q(s_i, a_i; \theta)]^2$

• $\frac{1}{|\mathcal{B}|} \sum_{i=|\mathcal{B}|}:$ Replay Buffer를 통해 minibatch를 사용하기에 생겨난 항이다.
• $\max_a \hat{Q}(s_{i+1}, a; \hat{\theta}):$ 일정 step동안 고정시켜 Non-stationary target problem을 해결한다.

🔻 Backward pass

$-\nabla_\theta L(\theta) = \frac{1}{|\mathcal{B}|} \sum_{i=|\mathcal{B}|} [r_{i+1} + \gamma \max_a \hat{Q}(s_{i+1}, a; \hat{\theta}) - Q(s_i, a_i; \theta)] \nabla_\theta Q(s_i, a_i; \theta)$

• Loss function을 $\theta$에 대해서 미분한다.
• DQN weight updata : $\theta := \theta - \alpha \nabla_\theta L(\theta)$

---

2️⃣ Diagram을 통한 DQN 작동방식 이해

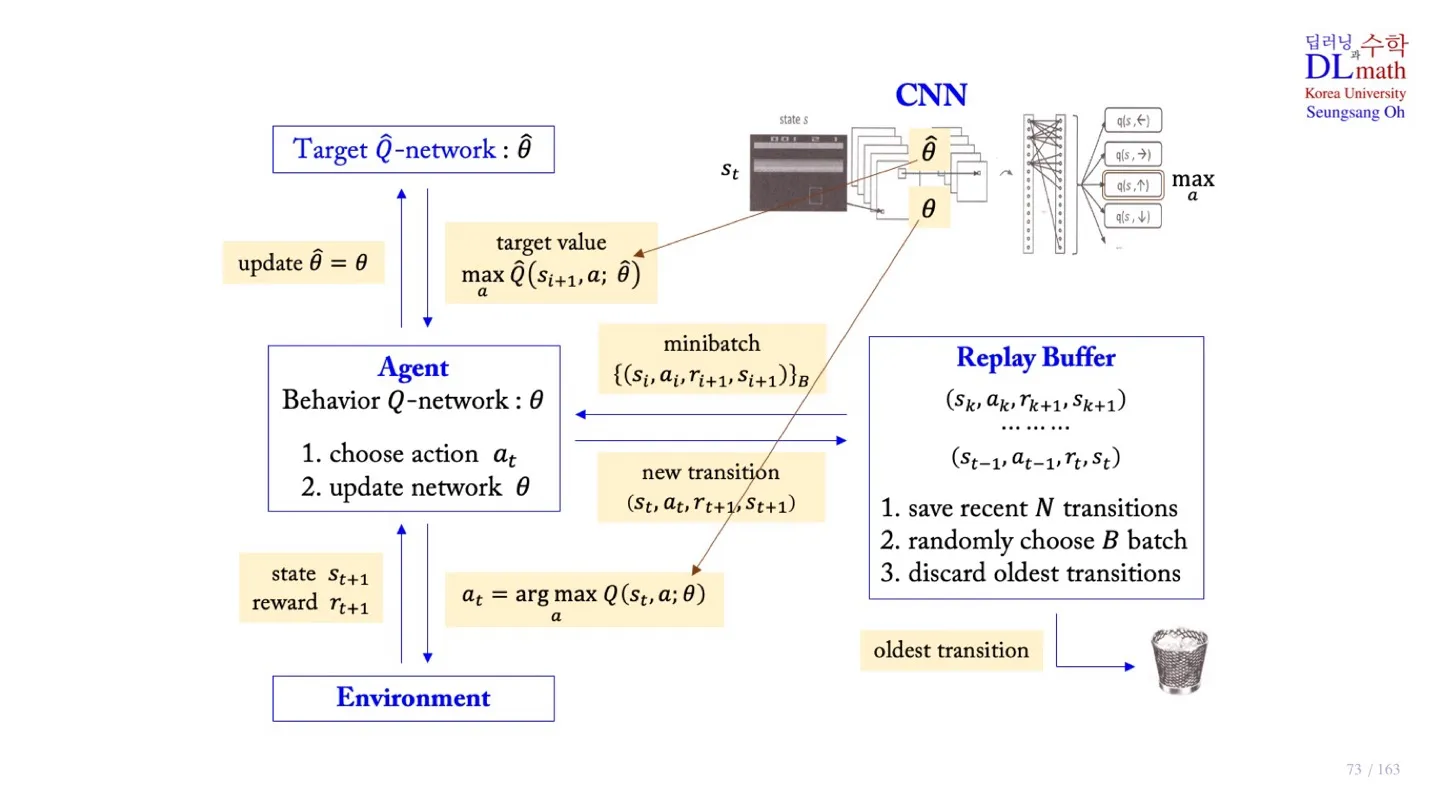
🔻 Sample을 얻는 과정

1. 주어진 state $s_t$에서 Behavior $Q$-Network $\theta$를 사용하여 Q-value를 구한다.
2. 가장 큰 action을 찾은 후, $\epsilon$-greedy policy를 통해 최종 aciton을 선택한다.
3. 해당 action을 Environment에 적용한다. (execute $a_t$ in emulator)
4. Reward $r_{t+1}$과 next state $s_{t+1}$을 얻는다.
5. 새로운 sample data $(s_t, a_t, r_{t+1}, s_{t+1})$를 Replay Buffer에 저장한다.
6. 저장된 data가 100,000개가 넘을 경우 가장 오래된 sample data를 제거한다.

🔻 Behavior $Q$-Network를 업데이트 하는 과정

5. Replay Buffer에서 minibatch 크기만큼 데이터를 sampling한다.

6. $-\nabla_\theta L(\theta) = \frac{1}{|\mathcal{B}|} \sum_{i=|\mathcal{B}|} [r_{i+1} + \gamma \max_a \hat{Q}(s_{i+1}, a; \hat{\theta}) - Q(s_i, a_i; \theta)] \nabla_\theta Q(s_i, a_i; \theta)$값을 계산한다.

7. Behavior $Q$-Network $\theta$를 $\theta := \theta - \alpha \nabla_\theta L(\theta)$ 방식으로 업데이트한다.

---

3️⃣ DQN의 pseudo code

📌 용어정리

$x_t :$ t번째 화면의 스크린 이미지

$\phi:$ 이미지 전처리 함수, 이미지를 gray scale에 84 X 84 pixel로 바꿔준다.

🔷 Pseudo Code

🔻 Initailize

• Behavior $Q$-Network $\theta$를 random하게 초기화한다.
• Target $\hat{Q}$-Network $\hat{\theta}$을 Behavior $Q$-Network $\theta$와 동일한 값으로 초기화한다.
• Replay Buffer의 크기 $N$을 지정한다.

🔻 Preprocessing

• 입력 이미지 $x_t$를 $s_t$로 정한 후 $\phi$를 통해 전처리한다.
• $\phi_t = \phi(s_t)$

🔻 Experience

• CNN $\theta$와 $\epsilon$-greedy policy를 통해 action $a_t$를 결정한다.
• $a_t$를 실행하여 Reward $r_{t+1}$과 next image $s_{t+1}$을 얻는다.
• $\phi$를 통해 $\phi_{t+1}$을 구한다.
• $(\phi_t, a_t, r_{t+1}, \phi_{t+1})$를 Replay Buffer에 저장한다.

🔻 Behavior $Q$-Network Update

• MiniBatch 수 $N$만큼 Replay Buffer에서 sampling한다.
• Target값 $y_i = r_{i+1} + \gamma \max_a \hat{Q}(s_{i+1}, a; \hat{\theta})$를 계산한다.
• $(y_i - Q(\phi_i, a_i,\ ;\theta)^2$에 gradient descent를 적용하여 Behavior $Q$-Network $\theta$를 업데이트 한다.

🔻 Target $\hat{Q}$-Network Update

• 일정 step $C$가 지날 때마다 $\hat{\theta} = \theta$ 로 업데이트 한다.

---

4️⃣ CNN in DQN

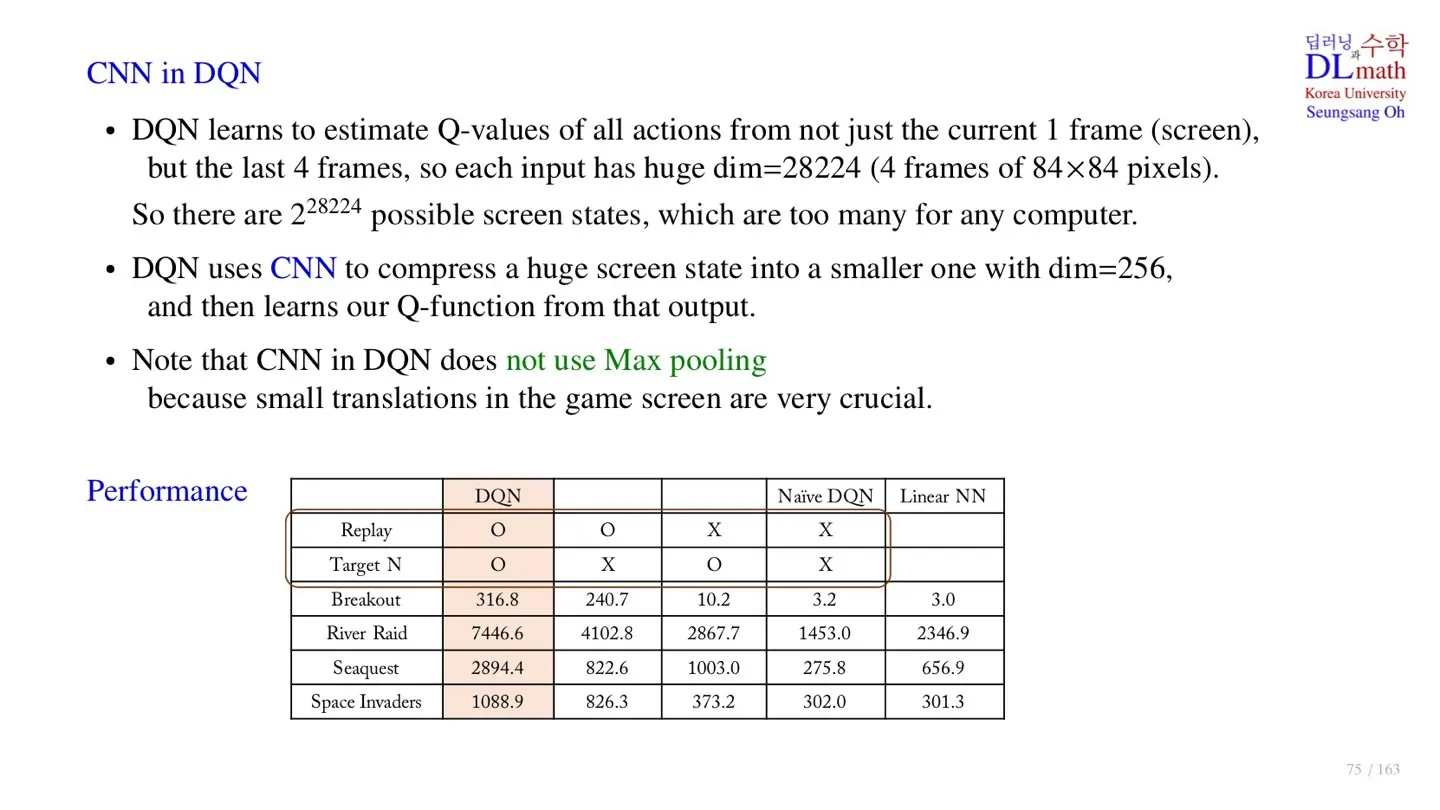
🔷 CNN을 통한 데이터 차원 축소

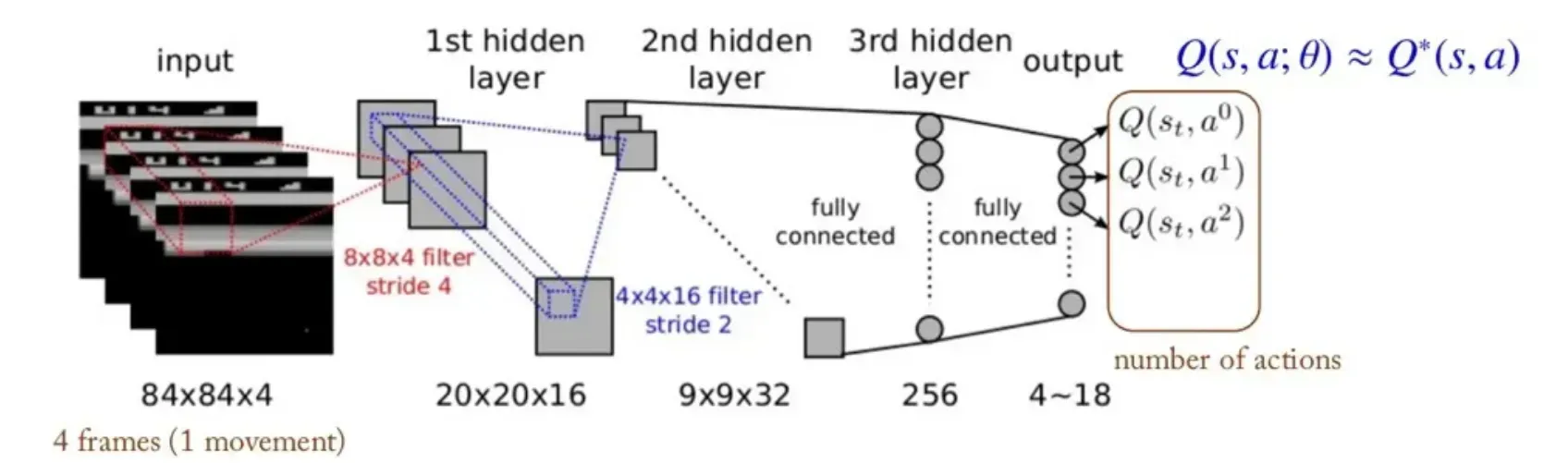
• 입력 데이터로 4개의 channel을 받는다. 이를 통해 객체의 움직임을 이해할 수 있다.
• $dim = 28224 = 4 \times 84 \times 84$
• Gray scale이기 때문에 가능한 screen state는 $2^{28224}$이다.
• Input data를 CNN layer를 통해 $dim = 256$의 데이터로 변환한다.

🔻 Max pooling을 사용하지 않는 이유

• Max pooling은 translation invariance를 위해 사용한다.
• 하지만 실제 game에서는 객체의 위치가 중요하기 때문에 DQN의 CNN에서는 max pooling을 사용하지 않는다.

🔷 성능 비교

	DQN			Naïve DQN	Linear NN
Replay	O	O	X	X
Target N	O	X	O	X
Breakout	316.8	240.7	10.2	3.2	3.0
River Raid	7446.6	4102.8	2867.7	1453.0	2346.9
Seaquest	2894.4	822.6	1003.0	275.8	656.9
Space Invaders	1088.9	826.3	373.2	302.0	301.3

---

5️⃣ 정리

🔷 18강에서 배운 내용은 아래와 같다.

1. Target Network를 적용하는 방법에 대해 배웠다.
2. Target Network를 위한 Loss function에 대해 배웠다.
3. Diagram을 통해 DQN의 작동원리를 살펴보았다.
4. DQN의 pseudo code에 대해 살펴보았다.
5. DQN 속 CNN의 역할과 특징에 대해 살펴보았다.