[Deep Reinforcement Learning] 20강 Dueling DQN

Woosci·2025년 7월 25일

강화학습

[Deep Reinforcement Learning]

목록 보기

19/33

👨‍🏫학습목표

오늘은 Dueling DQN의 구조와 한계, 한계를 극복하기 위한 방법에 대해 배워볼 예정이다.

👨‍🎓강의영상: https://www.youtube.com/watch?v=8E22UY6XXfc&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=20

📃 Dueling DQN 논문: https://arxiv.org/pdf/1511.06581

1️⃣ Dueling DQN

🔷 DQN 출력 살펴보기

🔻 기존의 DQN의 출력

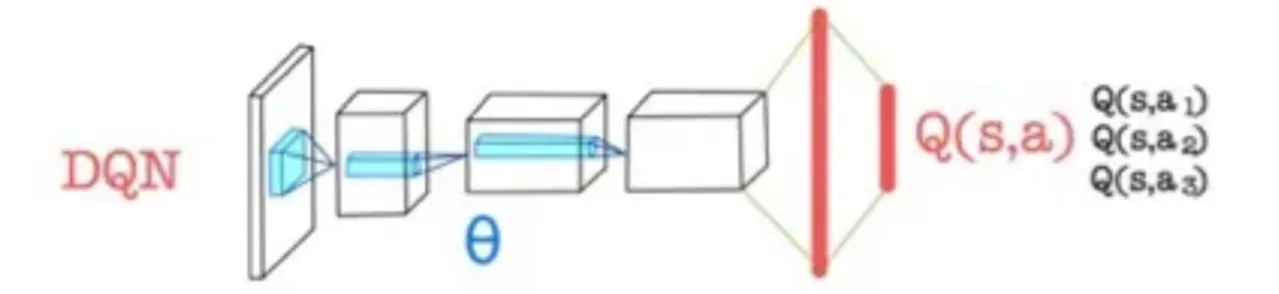
기존의 DQN은 입력된 State에서 취할 수 있는 모든 action에 대한 Q-value값을 출력한다.
Q-Network라고 한다.
CNN을 이용하여 이미지의 feature를 추출한 후 FC layer를 통해 Q-value를 출력한다.
CNN 부분을 CNN encoder라고 부른다.

🔻 Dueling DQN의 출력

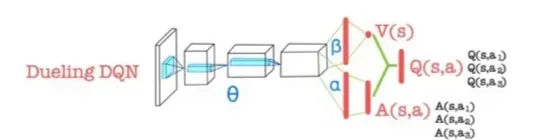
Dueling DQN은 Q-value값 대신 다른 2가지 값을 출력한다.
첫 번째는 advantage function value $A(s,a)$ 이고, 다른 하나는 state value $V(s)$ 이다.
Advantage function value $A(s,a)$ 는 모든 action에 대한 각각의 값이 출력된다.
state value $V(s)$ 은 action과 독릭적으로 하나의 값을 출력한다.
CNN encoder에서는 데이터를 하나의 파라미터 $\theta$ 로 처리한 후 FC layer에서 $\alpha, \beta$ 레이어로 개별적으로 처리된다.
$Q(s,a) = A(s,a) + V(s)$ 를 통해 구할 수 있다.
Advantage function value $A(s,a)$ 와 state value $V(s)$ 을 통해 $Q(s,a)$ 를 구하는 모듈을 aggregator라고 한다.

📕 Advantage function

$A_\pi(s, a) = q_\pi(s, a) - v_\pi(s)$

수식의 의미: 특정 action에서의 총 reward의 기대값과 모든 action의 총 reward의 기대값의 차이
$A_\pi(s, a) > 0$ 이면 해당 action이 평균보다는 좋은 선택이라는 의미이다.

🤔 Dueling DQN을 개발한 이유는 뭘까?

Dueling DQN이 기존의 DQN과 다른 점은 state value $V(s)$ 값을 출력한다는 것이다. 그렇다면 왜 state value $V(s)$ 값을 출력할까?

먼저 State value $V(s)$ 는 해당 state가 가치가 있는지 없는지 판단할 수 있다는 의미를 가진다.

일반적으로 강화학습에서는 state-action value $Q(s,a)$ 에 집중한다. 구체적인 값보다는 어떤 action을 선택할지 판단할 근거가 되기 때문이다.

그럼에도 불구하고 State value $V(s)$ 을 출력하는 이유는 다음 페이지에서 알아보자.

🔷 Dueling DQN의 특징

구체적인 내용은 향후 다룰 예정이다.

State-value $V(s)$ 를 알기 때문에 action이 environment에 영향을 크게 끼치지 않을 때도 state에 대한 평가가 가능하다.
Aggregator 모듈을 사용하기 때문에 Identifiability 문제가 발생한다.

$Q(s, a; \theta, \alpha, \beta) = V(s; \theta, \beta) + \left[ A(s, a; \theta, \alpha) - \frac{1}{|\mathcal{A}|} \sum_{a'} A(s, a'; \theta, \alpha) \right]$

위 수식을 통해 Identifiability 문제를 해결할 수 있다.

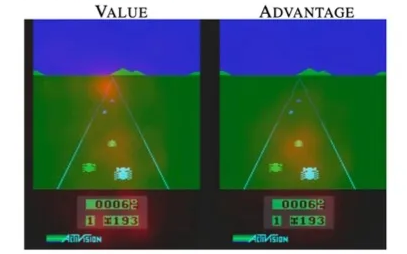
2️⃣ Value and advantage saliency map

붉은색으로 표시된 부분이 CNN 모델이 집중해서 보고 있는 곳이다.

🔷 첫 번째 그림

멀리서 장애물이 오고 있는 상황이다.
Advantage function은 크게 동작하지 않는다.
어떤 Action을 취해야 할지에 대한 정보가 중요하지 않은 대표적인 예시이다.
이러한 상황에서는 $Q(s,a)$ 보다 $V(s)$ 가 더 중요할 수 있다.

🔻 Advantage

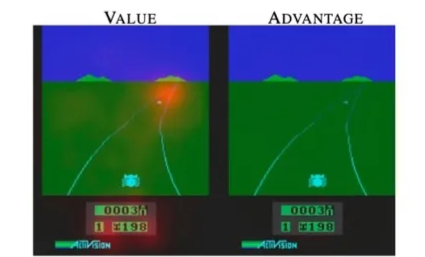
Advantage function은 현재의 action에 대한 보상을 중요시한다.
현재 장애물이 자동차 근처에 없기 때문에 어떠한 행동을 취해도 큰 문제가 없다.
따라서 모델이 크게 집중해야할 부분이 없다.

🔻 Value

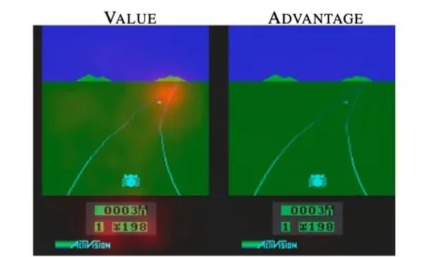
Value function은 Action과 관계없이 현재의 상황이 좋은지 좋지 않은지 평가한다.
바로 앞에는 장애물이 없기 때문에 집중하지 않고, 향후 다가올 장애물에 집중하고 있다.

🔷 두 번째 그림

바로 앞에 장애물이 존재한다.
첫 번째 그림과 달리 Advantage function이 잘 작동하고 있다.

🔻 Advantage

왼쪽 끝에 있는 장애물은 어느 정도 피하였기 때문에 새로 다가오는 장애물에 집중한다.

🔻 Value

멀리 있는 장애물과 가까이 있는 장애물을 모두 고려하고 있다.

🔷 Regular DQN vs Dueling DQN

🔻 Regular DQN

Regular DQN은 Q-value를 업데이트 한다.
이때 sample 데이터에 해당하는 $Q(s,a)$ 값만을 업데이트 한다.

🔻 Dueling DQN

Dueling DQN은 Advantage function과 State-value function을 학습한다.
이때 sample 데이터에 해당하는 $A(s,a)$ 값만이 업데이트 된다.
하지만 모든 $A(s,a)$ 를 구할 때 사용되는 $V(s)$ 값이 업데이트되기 때문에 전체 $Q(s,a)$ 를 조금씩 업데이트한 효과가 있다.

3️⃣ Identifiability Issue

📕 기본적인 이론

$Q^\pi(s,a) = V^\pi(s) + A^\pi(s,a)$

기본적을 Q-value는 state value와 advantage value의 합으로 구할 수 있다.

$V^\pi(s) = \mathbb{E}_{a \sim \pi(s)}[Q^\pi(s,a)]$

이때 현재 policy $\pi$ 에서 state value는 해당 state에서 취할 수 있는 모든 action value의 기대값으로 구할 수 있다.
이때 기대값은 각 action이 발생할 확률을 기준으로 만들어지며 state value는 해당 조건에 독립적이다.

$\mathbb{E}_{a \sim \pi(s)}[A^\pi(s,a)] = 0.$

첫 번째 수식의 양변에 action이 발생할 확률에 대한 기대값을 취해주면 Q-value function은 2번째 수식에 따라 Value function으로 변한다.
우변의 Value function을 action에 대한 확률과 무관하기 때문에 기대값에서 벗어난다.
양변의 value function을 제거하면 위 수식이 유도된다.

$a^* = \arg \max_{a'} Q(s,a')$

최적의 Policy를 구했다면 해당 policy의 각 state에서 최적의 action을 선택할 수 있다.

$Q(s,a^*) = V(s)$

Optimal policy에서는 Deterministic하게 작동하기 때문에 Q-value는 state value를 의미한다.

$A(s,a^*) = 0.$

따라서 첫 번째 수식에서 optimal policy를 적용하고 5번째 수식을 적용하면 위 수식이 유도된다.

🔷 Aggregating module

State value function과 Advantage function을 합하여 Q-value function을 구한다.

Q(s, a; \theta, \alpha, \beta) = V(s; \theta, \beta) + A(s, a; \theta, \alpha)

🔻 Identiability Issue

주어진 $Q(s,a)$ 를 통해 정확한 $V(s)$ 와 $A(s,a)$ 를 구하기 어렵다.

$Q(s, a) = (V(s) + \text{const}) + (A(s, a) - \text{const})$

Dueling DQN을 업데이트할 때는 $Q(s,a)$ 를 기준으로 업데이트를 진행한다.
따라서 $V(s)$ 와 $A(s,a)$ 에 대한 정보가 없다면 업데이트를 할 수 없다.

🔻 Solution

이를 해결하기 위해서는 $V(s)$ 나 $A(s,a)$ 중 한 가지가 정확한 기준점을 가지고 있어야 한다.
우리는 앞서 Optimal policy에서 Q-value는 state value를 의미함을 확인했다.

$Q(s, a; \theta, \alpha, \beta) = V(s; \theta, \beta) + \left[A(s, a; \theta, \alpha) - \max_{a'} A(s, a'; \theta, \alpha)\right]$

🤔 그런데 이 수식이 어떻게 Advantage와 Value state에 기준점을 제공할 수 있을까?

우선 생각해 볼만한 점은 모델이 Optimal 한 경우 state-value값이 Q-value값과 같아진다는 점이다.

$L(\theta) = \mathbb{E}_{(s,a,r,s') \sim \mathcal{D}} \left[ \left( \left( r' + \gamma Q\left(s', \arg \max_{a''} Q(s', a''; \theta); \hat{\theta}\right) \right) - Q(s, a; \theta) \right)^2 \right]$

DDQN의 Loss function이다.

이때 우리는 가장 오른쪽의 $Q(s, a; \theta)$ 값이 target값에 가까워지도록 학습한다.
그래서 $Q(s, a; \theta)$ 값을 gradient descent로 바꾸는데 이때 마주하게 되는 문제가 Identifiability Issue이다.

$Q(s, a) = (V(s) + \text{const}) + (A(s, a) - \text{const})$

$Q(s, a; \theta)$ 값을 변화시키기 위해 각 $V(s)$ 와 $A(s,a)$ 를 어떤 방향을 변화시켜야할지 알 수 없었기 때문이다. 그래서 Q-value값을 아래와 같이 정의한다.

$Q(s, a; \theta, \alpha, \beta) = V(s; \theta, \beta) + \left[A(s, a; \theta, \alpha) - \max_{a'} A(s, a'; \theta, \alpha)\right]$

이렇게 식을 설계하면 수집된 sample의 action이 optimal한 action과 같은 경우 0이 되어 학습은 $V(s)$ 만 이루어진다.
즉 Q-value값을 target값에 일치시키기 위해서 $V(s)$ 값을 변화시킨다.
Advantage function은 sample 데이터가 최적의 action이 아닌 경우만 target 방향으로 학습이 이루어진다.

🧐 그렇다면 어떻게 이 방식으로 $V(s)$ 값이 $Q(s,a)$ 값에 근사되도록 한다는 논리적 근거가 있을까?

$\frac{\partial Q}{\partial V(s)} = 1:$ Q-value $Q(s,a)$ 에 대한 $V(s)$ 의 기울기는 항상 1이므로 $V(s)$ 는 $Q(s,a)$ 의 차이를 대부분 그대로 가져와 학습한다.
$A(s,a)$ 는 optimal한 action과 차이가 있을 경우 학습이 이루어지며 target value에 대하여 현재 optimal advantage와의 오차를 학습합니다.
따라서 Q-value의 값은 대부분 state-value값을 통해 학습이 이루어져 $V(s)$ 값이 $Q(s,a)$ 값의 주된 가치를 학습하게 됩니다.

🔻 Max값을 쓰는 것의 한계

$Q(s, a; \theta, \alpha, \beta) = V(s; \theta, \beta) + \left[A(s, a; \theta, \alpha) - \max_{a'} A(s, a'; \theta, \alpha)\right]$

주어진 state에서 optimal한 action을 사용하는 것은 큰 변동성을 야기한다.
이는 학습의 불안정성으로 이어진다.

4️⃣ 개선된 Aggregating module

🔷 Mean을 사용한 Aggregating module

$Q(s, a; \theta, \alpha, \beta) = V(s; \theta, \beta) + \left[A(s, a; \theta, \alpha) - \frac{1}{|\mathcal{A}|} \sum_{a'} A(s, a'; \theta, \alpha)\right]$

Max 대신 mean을 사용하기 때문에 $A(s, a; \theta, \alpha)$ 에서 더 작은 값을 빼준다.
그 차이만큼 오차가 발생하지만 기본적으로 mean값이 더 변동성이 적기에 안정적인 학습이 가능하다.
또한 오차가 발생하더라도 Q-value는 그 값 자체보다 상대적 크기를 통해 optimal action을 선택하기 때문에 문제가 없다.

5️⃣ 정리

🔷 20강에서 배운 내용은 아래와 같다.

Dueling DQN의 구조에 대해 배웠다.

Dueling DQN에서 발생할 수 있는 Identifiability Issue에 대해 배웠다.

Identifiability Issue를 해결하기 위한 Aggregating module에 대해 배웠다.

안정적인 학습을 위한 개선된 Aggregating module에 대해 배웠다.

Woosci

I'm curious about AI

이전 포스트

[Deep Reinforcement Learning] 19강 DQN variant

다음 포스트

[Deep Reinforcement Learning] 20강 Dueling DQN